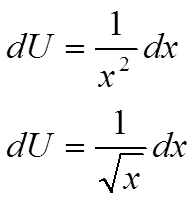Процесс принятия решения как один из этапов системного анализа. Полезность ожидаемых результатов. Уравнение Бернулли
Математическое описание эколог систем. Трофические функции. Квазимодели. Особенности моделирования процессов, протекающих с участием человека и живых организмов.
В основе моделирования этих с-м лежат модели, для кот. справедливы все з-ны сохран-я.
Для описания биол-х с-м необходимо соотношение, определяющих интенсивность потоков в-ва и энергии. Если рассматривать с-му из 2-х популяций, то кроме балансовых ур-й биомасс нужно знать скорость потребления жертвы хищником – трофическую ф-ю, кот. опред-ся многими сост-ми. По сути трофическая ф-я явл-ся усредненной по всей популяции, хар-ой поведения р-ий индивид-х организмов
Квазимодели:
Пи изучении сложных с-м сталкив. с недостатком инф. и устар-м материалом, кот. необход. для постр-я строгих мат-х моделей. В с-ме анализа приходится иметь дело с квазимоделями. субъективное представление изуч. в процессе, кот. возник-т у исслед-я на основе его опыта, интуиции, с-мы ассоциаций. Субъективные представления порождают приемы исследования, опред-ю психологию. В некоторых случаях эти приемы отражаются в системном анализе. СА занимается исследованием междисциплинарных проблем и связан с организ-й процедур принятия реш-й.
Особенности моделирования процессов протекающих с участием ч-ка.
В основе любых моделей лежат з-ны сохран-я, кот-е должны формулир-ся в терминах, опред-х наиболее существ-е стороны чел-й деят-и. При изуч-ии соц-х макросистем з-ны сохран-я должны формул-ся в экономич-х терминах и в экономике носят название баланса, но соотношение такого рода недостаточно для построения замкнутой модели. Значение многих вел-н нельзя опред-ть из балансовых соотношений, что усложняет описание процессов общественной природы. Одновременно с описанием процесса преобразования в-ва, энергии, движения нужно иметь модель инф-го процесса.
Уравнение «непрерывности». Распространение примесей в атмосфере (одномерный случай)
Математическое описание многих физических процессов сводится дифференциальных или интегро-дифференциальных уравнений. В частности, загрязнения воздушной среды от какого-либо источника можно описать, используя дифференциальные уравнения 2-го порядка. Загрязнение воздушной среды от источников описывается в рамках уравнения непрерывности.
Структура этого уравнения следующая:
dC/dt=[1]+[2]+[3]+[4];
1. – скорость изменения концентрации вследствие переноса воздушным потоком. 2. – скорость изменения концентрации обусловлено движением частиц относительно воздуха. 3. – скорость изменения концентрации связана с наличием источников загрязняющих веществ. 4. – скорость изменения, связанного с наличием стока (оттока ) з.в.
Фактически, плотность потока частиц равна числу частиц данного вида, пересекаемых в единицу времени единицу площади, расположенной перпендикулярно направлению потока. Для одномерного случая поток может быть диффузионным и конвективным:
dC/dt-div(J)
dC/dt=div(Jкон+J диф)
Для одномерного случая:
dC/dt=div(J)=div(C*U-D* dc/dx)=d/dx(C*U-D* dc/dx)=U dc/dx- D* d2c/dx2
если U=const D=const
Итак мы получаем:
dC/dt= d/dx(C*U)- D* d2c/dx2
U – скорость воздушного потока. D – коэффициент диффузии., div –изменение плотности потока в пространстве.
Процесс принятия решения как один из этапов системного анализа. Полезность ожидаемых результатов. Уравнение Бернулли.
Процесс принятия решения.
Этот этап это выбор наиболее желательного варианта решения который осуществляется путем анализа возможных вариантов решения нужными данными явл соотношения между входными и выходными переменными и выходные переменные задаваемые группами лиц с общими интересами.
Предпочтительность задают в общем виде, поэтому показатели сист сводятся к 1 скалярной величине, для этого вводят сист оценок показателей для групп лиц с общими интересами. Для каждого случая исп объективную инф получаемую при моделировании т.е. связывающее его решение с последствиями, а также субъективных данных которые получают с помощью сист оценок для группы лиц с общими интересами. Одним из способов анализа явл материальная субъективная инф не учитывается в процессе принятия решения, но учитывается в процессе принятия решения такой способ искл необходимость принятия решений с учетом четкого определения индивид оценок, др способ использования субъект инф состоит в том что исследователи пытаются определить мнения своих заказчиков, при этом используют данную ими оценку. Для классификации показателей для их значимости или для присвоения им весовых множителей рекомендует группа лиц с общими интересами единственного варианта решения.
Каждый из способов имеет свои преимущества и недостатки. Иногда трудно определить индивидуальную оценку но когда это удается установленная оценка может не отражать действительное мнение людей, это связано с тем что оценка даваемая в анкете может не отражать фактическую реакцию человека, его действия в соот-вии ситуации принятия решения. Необходимо учитывать что при наличии групп лиц с одинаковыми интересами нет равновесия для показателя который был бы приемлемым для всех групп. Трудность связана с допущением относительно предпочтительности действий людей в будущем. Несмотря на это эти методы нужно учитывать на основе сущест-х принципов и методов их учета т.к. в противном случае на процесс принятия решения будет оказывать влияние мнение авторитетных лиц, убежденность, красноречие людей представляющих группы с разными интересами
Полезность ожидаемой информации (ожидание результатов).
Полезность – это число, приписываемое рабочей хар – ке и которое представляет собой оценку значимости этого результата по восприятию определ группы лиц или человеком или человеком. Бернулли более 200 лет назад рассматривал вопрос о полезности богатства, вывел, что приращение полезности обратно пропорционально богатству человека и на основе этого вывел соотношение:
dU=b/xdλ ,где U-приращение полезности; х- богатство U=blnx+ C в,с=const, если в=1,с=0 U=lnx
Последователи Бернулли предложили другие зависимости: