Типичные ЗЛП и их математические модели

Глава I. Линейное программирование

Задача линейного программирования. Типичные задачи линейного программирования, их математические модели.

Задача линейного программирования

Как известно, задача нахождения экстремумов функций нескольких переменных имеет вид

f(x₁, x₂, …, x_n) ® min (max)

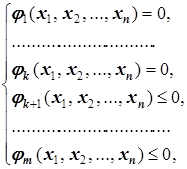(1.1)

где f, j_i (i=1, 2, …, m) - некоторые функции из R^п в R. Если все эти функции линейны, то задача (1.1) называется задачей линейного программирования (ЗЛП).

Таким образом, ЗЛП имеет вид:

c₁x₁+c₂x₂+…+c_nx_n®max(min)

(1.2)

Специфика многих задач производственного характера заключается в том, что на переменные накладываются определённые ограничения (условия), вытекающие из их содержания. Например, если x_j (j=1, 2, …, n) выражает количество выпускаемой продукции, то оно должно быть неотрицательным: x_j≥0. Может оказаться, что выпускаемая продукция не может быть выражена в дробных числах (например, число выпускаемых автомобилей). В этом случае x_jÎZ. В методах оптимизации мы ограничимся задачами вида

c₁x₁+c₂x₂+…+c_nx_n®max(min)

(1.2)

и под общей ЗЛП будем подразумевать эту задачу.

Типичные ЗЛП и их математические модели

1. Задача об использовании сырья. Некоторое производство выпускает n видов продукции с использованием m видов сырья. Известны: a_ij - количество i-го вида сырья, затрачиваемого на выпуск единицы продукции j-го вида; b_i - запасы i-го вида сырья; c_j - прибыль от реализации единицы продукции j-го вида. Составить план производства продукции (то есть определить, в каком количестве выпустить каждого вида продукции), обеспечивающий максимальную прибыль.

Составим математическую модель задачи.

Обозначим через x_j количество выпускаемой продукции j-го вида; x₁ - количество выпускаемой продукции 1-го вида, x₂ - количество выпускаемой продукции 2-го вида и т.д. Тогда c₁x₁ - прибыль от реализации всей произведённой продукции 1-го вида, и, вообще, c_jx_j - прибыль от реализации всей произведённой продукции j-го вида, c₁x₁+c₂x₂+…+c_nx_n - общая прибыль от реализации всей произведённой продукции. Это - целевая функция, максимум которой мы должны получить: c₁x₁+c₂x₂+…+c_nx_n®max.

Количество сырья первого вида, затрачиваемого на выпуск единицы продукции первого вида, равно a₁₁, x₁ - количество выпускаемой продукции первого вида. Поэтому всего сырья первого вида на выпуск всей продукции первого вида уйдёт в количестве a₁₁x₁. Аналогично, a₁₂x₂ - общее количество сырья первого вида, которое уйдёт на впуск всей продукции второго вида и т.д. Всего же количество сырья первого вида, которое уйдёт на производство всех видов продукции, равно a₁₁x₁+a₁₂x₂+…+a_1nx_n, и оно не может превосходить общие запасы сырья первого вида, то есть b₁: a₁₁x₁+a₁₂x₂+…+a_1nx_n≤b₁. Аналогично рассуждая в общем случае относительно i-го вида сырья, получим неравенство a_i1x₁+a_i2x₂+…+a_inx_n≤b_i (i=1, 2, …, m). Наконец, количество выпускаемой продукции j-го вида не может быть отрицательным: x_j≥0 (j=1, 2, …, n). И мы приходим к следующей математической модели задачи:

c₁x₁+c₂x₂+…+c_nx_n®max

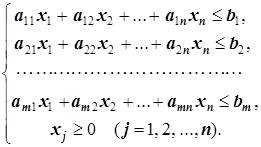(1.4)

2. Задача о составлении рациона (задача о диете). Сельхозпредприятие занимается откормом скота. В откормочный рацион входит n видов продуктов, которые содержат m видов питательных веществ. Известны: a_ij - количество i-го вида питательного вещества в единице продукта j-го вида; b_i - необходимое количество питательного вещества i-го вида, содержащегося в рационе; c_j - стоимость единицы продукта j-го вида. Составить рацион (то есть определить, в каком количестве включить в рацион продукта каждого вида), при котором достигается минимальная стоимость рациона.

Составим математическую модель задачи.

Обозначим через x_j количество продуктов j-го вида, включаемого в рацион. Тогда c₁x₁+c₂x₂+…+c_nx_n - общая стоимость рациона, которая должна быть минимальной: c₁x₁+c₂x₂+…+c_nx_n®min.

Количество питательного вещества первого вида, входящего в единицу продукта первого вида, равно a₁₁, x₁ - количество продукта первого вида, входящего в рацион. Поэтому всего питательного вещества первого вида, входящего в рацион с продуктами первого вида, составит a₁₁x₁. Аналогично, a₁₂x₂ - общее количество питательного вещества второго вида, входящего в рацион с продуктами второго вида, и т.д. Всего же количество питательного вещества первого вида, которое поступит в рацион со всеми видами продуктов, равно a₁₁x₁+a₁₂x₂+…+a_1nx_n, и оно не может быть меньше положенного количества, то есть b₁: a₁₁x₁+a₁₂x₂+…+a_1nx_n≥b₁. Аналогично рассуждая в общем случае относительно i-го вида питательных веществ, получим неравенство a_i1x₁+a_i2x₂+…+a_inx_n≥b_i (i=1, 2, …, m). Наконец, количество продуктов, входящих в рацион, не может быть отрицательным: x_j≥0 (j=1, 2, …, n). И мы приходим к следующей математической модели задачи:

c₁x₁+c₂x₂+…+c_nx_n®min

(1.5)

Упражнения.

1) Какие из следующих задач являются задачами линейного программирования, какие нет:

а) -2x₁+x₂+8x₃-2x₄®min б) -2x₁+ 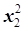+8x₃-2x₄®min

в) -3x₁-2x₂+x₃®min(max) г) 4x₁+x₂®min(max)

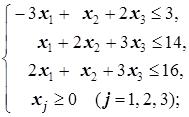
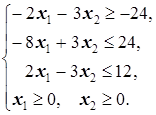
д) -3x₁-2x₂+x₃®min(max) е) 4x₁+x₂®min(max)

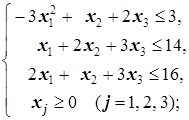
ж) -3x₁+x₂+2x₃®max(min) з) -3x₁+2x₂+2x₃®max(min)

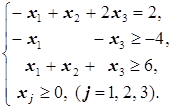
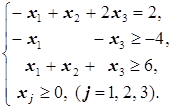
Решение. а) задача является задачей линейного программирования, так как и целевая функция -2x₁+x₂+8x₃-2x₄, и функции и в ограничениях линейные.

б) Задача не является задачей линейного программирования, так как целевая функция не является линейной - переменная x₂ входит в функцию в квадрате: .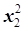

Составить математические модели следующих задач:

2) При производстве двух видов продукции используется три вида сырья. Составить план выпуска продукции, обеспечивающий максимум прибыли. Исходные данные приводятся в таблицах:

а)	Запасы сырья	Расход сырья на единицу продукции	б)	Запасы сырья	Расход сырья на единицу продукции
	№1	№2		№1	№2
	Прибыль				Прибыль

3) В рационе животных используется два вида кормов. Животные должны получать три вида питательных веществ. Составить рацион наименьшей стоимости. Исходные данные приводятся в таблицах:

а)	Необходимое количество пит. вещ-тв	Содержание пит. вещ-ва в ед-це корма	б)	Необходимое количество пит. вещ-тв	Содержание пит. вещ-ва в ед-це корма
	№1	№2		№1	№2
	Стоимость ед-цы корма				Стоимость ед-цы корма