Теплота. Температура. Температурное поле

ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕПЛООБМЕНА

Все изучаемые нами тела имеют различную температуру, т. е. они обладают различной внутренней энергией. Температура тела, выражающая степень его нагретости, является физической характеристикой запаса внутренней энергии, обусловленной кинетической энергией молекул этого тела. Чем выше температура тела, тем больший запас внутренней (тепловой) энергии оно имеет. Из опыта известно, что эта энергия передается от более нагретого тела к менее нагретому или от области тела с более высокой температурой к области с менее высокой. Количество передаваемой энергии в этом процессе называют количеством теплоты.

Таким образом, теплота – синонимы: тепловая энергия, тепло — один из видов энергии, которая представляет собой кинетическую энергию микрочастиц, в основном молекул. Тепловая энергия может превращаться в химическую энергию при изменении агрегатного состояния тела. Например, для того чтобы превратить лед в воду, нужно затратить некоторое количество теплоты; при этом тепловая энергия «уничтожается», а взамен возникает химическая энергия, которую часто называют скрытой теплотой (хотя в действительности теплоты уже не существует, а имеется лишь возможность при определенных условиях превращения химической энергии вновь в тепловую).

Другим видом превращения теплоты является ее переход в электромагнитную энергию. Например, нагретое тело излучает (теряет) тепловую энергию, при этом теплота нагретого тела превращается в электромагнитную энергию.

Кинетическая энергия микрочастиц (т.е. теплота) может превращаться и в механическую (кинетическую или потенциальную) энергию микрочастиц тела; еще чаще встречаются обратные переходы – механической энергии в тепловую, например, при движении воды (диссипация энергии).

Все переходы энергии из одного вида в другой, естественно, подчиняются закону сохранения энергии, что служит основой для составления уравнения энергетического баланса (Лекция №6).

Производными от теплоты являются такие понятия, как

· тепловой поток – количество теплоты, проходящей через изотермическую поверхность в единицу времени;

· интенсивность (плотность) теплового потока – тепловой поток, проходящий в единицу времени через единицу площади изотермической поверхности;

· мощность источника теплоты – количество теплоты, выделяющейся в единицу времени в точке, на поверхности или в объеме;

· теплосодержание – количество теплоты, содержащейся в теле.

Процесс передачи теплоты в природе от одного тела к другому довольно сложный и часто осуществляется одновременно несколькими путями.

Общее количество передаваемой теплоты измеряется в джоулях (Дж) и обозначается через Q. Джоуль — это единица работы (энергии), произведенной силой в 1 H на пути в 1 м, в случае, когда сила и путь совпадают по направлению.

Индексом Q будем обозначать и количество внутренней энергии (теплоты), которым обладает тело при данной температуре t. Эту энергию принято называть энтальпией. Для однородного тела ее определяют по формуле

Q=crVt, (3.1)

где с — удельная теплоемкость материала тела (см. Лекцию №2); r — плотность материала тела; V — объем тела; m=rV — масса тела.

Энтальпия, как и количество теплоты, измеряется в джоулях.

Из практики известно, что каждая точка природных объектов (грунт, лед, снег, вода и другие вещества) и инженерных сооружений (плотина, разделяющая стенка, трубопровод, железнодорожная насыпь и др.) характеризуется температурой.

Температура – физическая величина, характеризующая тепловое состояние микроскопических объемов тела. Температура позволяет судить не только о тепловой энергии тела, но и о возможностях отдачи или получения тепловой энергии извне, о перераспределении теплоты внутри тела и ее переходе в другие виды энергии.

Два тела могут иметь одинаковую тепловую энергию, но различную температуру; при этом их состояния оказываются весьма разными. Это, прежде всего, различие состояния в данный момент времени, но не менее важно различие, которое представляют оба объекта по вероятности дальнейшего хода тепловых процессов. Так, если имеется водохранилище глубиной 100 м с температурой воды 0,5°С и водохранилище глубиной 10 м с температурой воды 5°С, то хотя их запасы теплоты одинаковы (относительно температурного порога льдообразования – 0°С), при прочих равных условиях ледяной покров раньше образуется на первом водохранилище. Однако даже при одинаковых глубинах и равных запасах тепла условия в двух водохранилищах могут быть весьма разными из-за разного характера распределения температуры по глубине.

Если температура тела изменяется от точки к точке, то оно может быть охарактеризовано пространственным температурным полем, а если температура изменяется к тому же и во времени, то пространственно-временным. Температурное поле может быть представлено в виде функциональной зависимости

t =f₁ (x, у, z, τ), (3.2)

где х, у, z — координаты точки; τ — время.

Таким образом, совокупность температур всех точек тела в какой-либо момент времени называется температурным полем.

Температурные поля подразделяют на стационарные и нестационарные. Если температура тела является функцией координат и времени, что соответствует зависимости (3.2), то такое температурное поле будет нестационарным (градиент температуры по времени ∂t/∂τ ≠ 0). В том случае, когда температура тела с течением времени не изменяется (∂t/∂τ = 0) и является функцией только координат, температурное поле будет стационарным:

t =f₂ (x, у, z). (3.3)

Различают температурные поля трехмерные (пространственные), двухмерные (плоские) и одномерные (линейные). К первым относятся поля, описываемые зависимостями (3.2) и (3.3), ко вторым — поля, описываемые зависимостями:

t =f₃ (x, у, τ), (3.4)

t =f₄ (x, у), (3.5)

к третьим — поля, описываемые зависимостями:

t =f₅ (x, τ), (3.6)

t =f₆ (x). (3.7)

Соединим в двухмерном температурном поле точки с одинаковой температурой — получим систему линий, соответствующих выбранной температуре. Эти линии называются изотермами. Они не пересекаются и заканчиваются на контуре или же замыкаются сами на себя (рис. 3.1).

Выделим какие-либо две расположенные рядом изотермы, например, с температурой t и t - ∆t, и проследим между ними расстояние ∆n. Оно окажется различным.

Отношение перепада температуры ∆t к расстоянию между изотермами ∆n по нормали n при стремлении ∆n к нулю называют градиентом температуры, т. е.

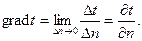
(3.8)

Градиент температуры наибольший там, где расстояние по нормали между изотермами наименьшее, и наоборот.

Градиент температуры — вектор, направленный по нормали к изотерме в сторону возрастания температуры. Поэтому в направлении убывания температуры он отрицательный.

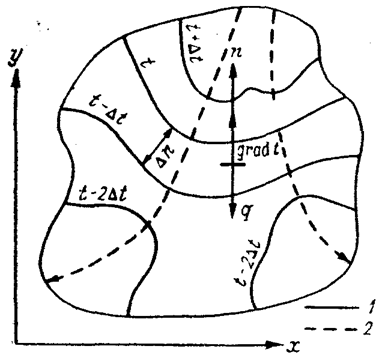
Рис. 3.1. Двухмерное температурное поле (водоем в плане) [8]

1 — изотерма, 2 — линия тока теплоты.

Температурное поле дает исчерпывающую информацию о тепловом состоянии тела и обладает следующими свойствами:

· температура в теле меняется во всех направлениях непрерывно; никаких скачков температуры в теле нет;

· между точками, имеющими разные температуры, непременно имеются точки со всеми промежуточными температурами;

· изотермические поверхности всегда замкнуты на себя или на границы тела;

· любое тело может быть представлено как совокупность бесконечного числа примыкающих друг к другу изотермических поверхностей;

· изотермические поверхности не могут пересекать друг друга (так как одна и та же точка тела не может иметь одновременно две температуры), но одно тело может иметь несколько одинаковых изотерм;

· поверхности максимальных градиентов не имеют разрывов, но могут иметь изломы и, кроме того, в отличие от изотермических поверхностей значения градиентов могут меняться скачкообразно;

· в твердом изотропном теле поверхности максимальных градиентов являются одновременно поверхностями, совпадающими с направлением теплового потока.