Численное решение задачи Коши для скалярного обыкновенного дифференциального уравнения.
Найти численное решение обыкновенного дифференциального уравнения в MathCAD можно разными способами. Рассмотрим случай, когда задан отрезок, на котором требуется построить решение, и значение неизвестной функции в начальной точке (на левом конце отрезка).
I. Алгоритм решения задачи Коши обыкновенного дифференциального уравнения с использованием «блока решений»:
1. Ввести ключевое слово Given, с которого начинается блок решений.
2. Записать уравнение, используя знак логического равенства между правой и левой частями уравнения с панели управления Evaluation (Выражения).
3. Задать начальные значения переменной, которая есть в уравнении.
4. Ввести ключевое слово Odesolve, которым заканчивается блок решений, то есть присвоить функции, относительно которой решается уравнение, значение Odesolve с параметрами интервала интегрирования.
5. Определить значение найденной функции в точках интервала, для чего создать соответствующий цикл.
6. Построить и отформатировать график найденной функции в точках интервала.
II. Алгоритм решения задачи Коши для обыкновенного дифференциального уравнения с использованием встроенной функции (например rkfixed).
1. Задать начальные значения переменной, которая есть в уравнении.
2. Записать уравнения, используя знак логического равенства между правой и левой частями уравнения с панели управления Evaluation (Выражения).
3. Задать количество шагов интегрирования уравнения на интервале.
4. Присвоить функции, относительно которой решается уравнение, значение rkfixed с параметрами: функция, интервал интегрирования, количество шагов на интервале интегрирования, оператор дифференциального уравнения.
5. Определить значение найденной функции в точках интервала, для чего создать соответствующий цикл.
6. Построить и отформатировать график найденной функции в точках интервала.
Пример
I.Найдем решение обыкновенного дифференциального уравнения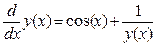 
на интервале [0,100] с начальным условием у(0)=1, следуя алгоритму:
1. Ввести ключевое слово Given.
2. Записать уравнение, используя логический знак равенства:
.
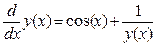3. Записать начальное условие, используя логический знак равенства:
у(0)=1.
4. Найти решение задачи с помощью функции Odesolve:
у:=Odesolve(x,100).
5. Создать цикл для построения графика решения:
x:=0,..100.
6. Построить график и отформатировать его.
 |
 |
 |
 |
 |
 |
 |
 |
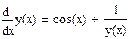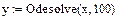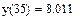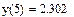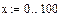II. Найдем для той же задачи решение с использованием встроенной функции rkfixed:
1. Задать начальное условие
у(0)=y0:=0.1.
2. Задать функцию, определяющую правую часть дифференциального уравнения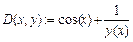 
.
3. Указать количество шагов интегрирования К:=100.
4. Найти решение задачи с помощью функции rkfixed. Знак равенства выбирается на панели Логика (Логические).
у=rkfixed(у0, х1,х2,К, D).
5. Создать цикл для построения графика решения:
х:=0,..100.
6. Построить график функции в точках интервала и отформатировать его.
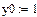
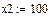
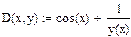
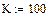
Примечание: результаты решения дифференциального уравнения двумя подходами должны совпадать.
Отметим, что MathCAD содержит и другие встроенные функции для решения дифференциальных уравнений:
- Rkadapt – метод Рунге-Кутта с переменным шагом интегрирования (величина шага адаптируется к скорости изменения функции решения, то есть при быстром изменении шаг уменьшаем);
- Bulstoer – метод Булирша-Штера (более эффективен в случае, если решение является плавной функцией).
Эти функции имеют сходные параметры (y0, a, b, n, D):
- y0 – вектор начальных значений неизвестных функций, входящих в систему (в случае одного уравнений и одной неизвестной функции – это просто число);
- a – начало отрезка, на котором ищется решение (именно в этой точке задается значение вектора y0);
- b – конец отрезка интегрирования;
- n – количество частей, на которые разбивается отрезок интегрирования;
- D(x, y) – векторная функция, элементы которой содержат правые части уравнений системы в нормальной записи (когда левые части – производные от соответствующих функций, а в правых частях производные отсутствуют)