Теплообмен излучением при наличии экранов

В различных областях техники часто встречаются случаи, когда требуется уменьшить передачу теплоты излучением. Например, нужно оградить рабочих от действия тепловых лучей в цехах, где имеются поверхности с высокими темпе ратурами.

В других случаях необходимо оградить деревянные части зданий от энергии излучения, чтобы предотвратить воспламенение. Следует защищать от энергии излучения тер­мометры, так как в противном случае они дают неверные показания. Поэтому всегда, когда необходимо уменьшить пере­дачу теплоты излучением, прибегают к установке экранов. Обычно экран представляет собой тонкий металлический лист с большой отражательной способностью. Рассмотрим действие экрана между двумя плоскими безграничными параллельными поверхностями (рис. 2.11).

Рассматриваемая излучающая система состоит из сово­купности систем а и б, для которых может быть использована ранее полученная зависимость, выражающая результирующее излучение:

Здесь по условиям задачи ; кроме того, для стационарного режима . Тогда из уравнения найдем T :

Подставляя одно уравнение в другое, получаем плотность потока результирующего излучения

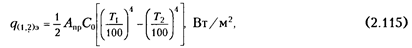
где приведенная поглощательная способность A системы тел 1 и 2 определяется согласно зависимости. Сравнение с зави­симостью для системы тел без экрана показывает, что при наличии одного экрана лучистый поток уменьшается в два раза.

Можно доказать, что установка двух экранов уменьшает теплоотдачу втрое, трех экранов - вчетверо и т.д.

Следовательно, при наличии п экранов результирующий тепловой поток уменьшится в (п + 1) раз:

2.3.4. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ
МЕЖДУ ТЕЛОМ И ЕГО ОБОЛОЧКОЙ

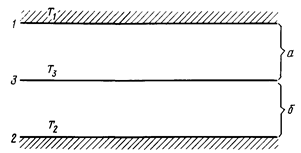
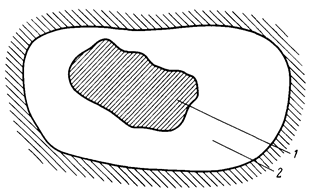
Рассмотрим два тела, из которых одно находится в плоскости другого (рис. 2.12).

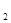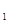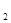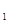Первое тело выпуклое, а второе вогнутое. Они имеют заданные поверхности H , и H поглощательные способности A , и A , степени черноты , и , а также температуры T , и T 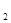, причем 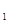T > T .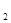

Для определения искомой величины результирующего потока излучения используем зависимость

В общем случае плотность потока результирующего излучения определяется разностью встречных потоков излучения, падающих на условную поверхность. При наличии диаметрической промежуточной среды можно записать:

где 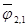^- средний угловой коэффициент излучения.

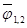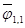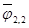
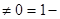
Он характеризует часть потока эффективного излучения, которая падает со второго тела на первое, по отношению к полному потоку эффективного излучения. Угловой коэффициент = 1, так как энергия, излучаемая первым телом, целиком падает на второе тело. Угловой коэффициент = 0 в соответствии с принятым допущением, что первое тело выпуклое. Величина 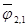, характеризует долю энергии излучения второго тела само на себя.

Для определения потока результирующего излучения используем метод Сальдо. Тогда в соответствии с зависимостью

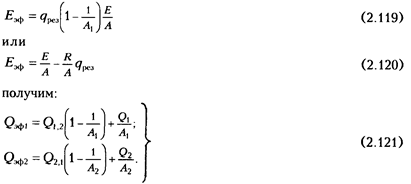
Подставим в зависимость (2.121) соотношения (2.119) и (2.120). Учитывая, что при стационарном режиме резуль­тирующие потоки излучения равны, получаем

Потоки собственного излучения могут быть выражены по закону Стефана - Больцмана через заданные температуры:

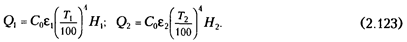
Подставив формулы (2.123), получим

Для определения неизвестной величины 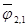положим временно, что температуры первого и второго тел одинаковы (T 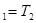). В этом случае Q 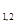= 0.

Таким образом, в общем случае угловой коэффициент излучения зависит от геометрических свойств излучающей системы и ее оптических свойств. Следовательно, используя уравнение (2.124), поток результирующего излучения можно выразить, разделив числитель и знаменатель на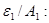

Обычно полагают 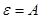, тогда (2.126) переходит в соотношение

и средний угловой коэффициент излучения превращается в чисто геометрическую характеристику.

Выражение для результирующего потока излучения в этом случае принимает вид

или в более короткой записи

где приведенная поглощательная способность системы тел

Если А 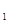= 1 или , то . Введем понятие приведенного коэффициента излучения системы С, а, Вт/(м² • К⁴):

Тогда вместо (2.130) получим

В частном случае, когда поверхности H угловой коэффициент излучения 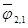= 1. Это означает, что вся энергия с тела 1 попадает на тело 2, и мы переходим к решению, полученному выше для плоскопараллельной системы тел.

Если одно тело мало по сравнению с другим (H ), то , а 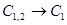. Этот же результат получают при 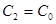из формулы (2.130).

Приведенные зависимости для Q 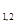справедливы для концентрического и неконцентрического расположения сферических поверхностей, а также произвольных изогнутых тел с оболочкой.