Моделирование двигателя постоянного тока с независимым возбуждением
Цель работы: изучение библиотек System View; представление результатов моделирования в окне анализа; моделирование режимов «Пуск», «Реверс», «Торможение»; моделирование нагрузок.
Двигатель постоянного тока независимого возбуждения (ДПТ НВ) это электрическая машина, имеющая две электрически несвязанные обмотки – обмотку возбуждения, расположенную на статоре машины, и обмотку якоря, расположенную на роторе (якоре) машины. Передача электрической энергии к якорю происходит посредством щеточно-коллекторного узла. Обмотки электрической машины питаются от источника постоянного напряжения. Электрическая функциональная схема ДПТ НВ представлена на рисунке 5.1.
 |
| Рисунок 5.1 – Электрическая функциональная схема ДПТ НВ |
Уравнения, описывающие электромеханическое преобразование энергии в ДПТ НВ, имеют вид:
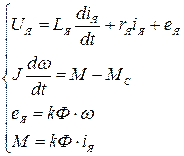 . (5.1)
. (5.1)
Уравнения (5.1) могут быть представлены в операторной форме:
 . (5.2)
. (5.2)
Уравнениям (5.2) соответствует структурная схема ДПТ НВ (рис. 5.2).
 |
| Рис. 5.2. Структурная схема ДПТ НВ |
Расчет коэффициентов и постоянных времени
Номинальная скорость вращения двигателя и конструктивный коэффициент:
 ;
; 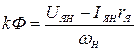 , (4.3)
, (4.3)
где nН – номинальная скорость вращения в оборотах за минуту;
wН – номинальная скорость вращения в радианах за секунду;
UЯН – номинальное напряжение якоря;
IЯН – номинальный ток якоря;
rЯ – сопротивление якорной цепи.
Индуктивность якорной цепи определяется по формуле Ленвилля-Уманского
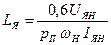 . (4.4)
. (4.4)
Электромагнитная и электромеханическая постоянные времени:
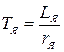 ,
, 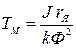 . (4.5)
. (4.5)
Определяется коэффициент демпфирования:
 . (4.6)
. (4.6)
Если коэффициент демпфирования меньше единицы, то двигатель может быть представлен колебательным звеном. В этом случае шаг интегрирования выбирается на основании собственной постоянной времени двигателя:
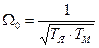 ,
, 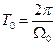 . (4.7)
. (4.7)
Если коэффициент демпфирования больше единицы, то двигатель представляет инерционное звено второго порядка. Поэтому шаг интегрирования выбирается на основании минимальной постоянной времени ДПТ (TЯ или TM) и должен быть как минимум в три раза меньше соответствующей постоянной времени двигателя.
Ход работы
1. По структурной схеме (рис. 5.2) в пакете SV составить модель двигателя постоянного тока. Данные для расчёта параметров двигателя представлены в приложении А (табл. 1).
2. Отладить модель, исследуя пуск двигателя в режиме холостого хода. Момент сопротивления на валу двигателя принять равным нулю: MC = 0, а напряжение якоря равным номинальному UЯ = UЯН .
3. Исследовать режимы «Пуска» и «Реверса» двигателя с активной нагрузкой на валу. Момент сопротивления на валу принять равным номинальному моменту двигателя: MC = MН.
4. Исследовать режимы «Пуска» и «Реверса» ДПТ при реактивном характере нагрузки на валу. Момент сопротивления на валу принять равным номинальному моменту двигателя: MC = MН.
Содержание отчета
1. Схема и математическое описание ДПТ НВ.
2. Структурная схема модели ДПТ НВ.
3. Расчет коэффициентов и постоянных времени двигателя. Выбор шага интегрирования.
4. Схемы модели двигателя в пакете System View для заданных режимов работы.
5. Графики переходных процессов «Пуска» и «Реверса» двигателя для холостого хода, активной и реактивной нагрузки.
