Повторение испытаний. Формула Бернулли

Если производится некоторое количество испытаний, в результате которых может произойти или не произойти событие А, и вероятность появления этого события в каждом из испытаний не зависит от результатов остальных испытаний, то такие испытания называются независимыми относительно события А.

Допустим, что событие А наступает в каждом испытании с вероятностью 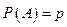. Определим вероятность того, что в результате п испытаний событие А наступило ровно т раз.

Эту вероятность в принципе можно посчитать, используя теоремы сложения и умножения вероятностей, аналогично тому, как это делалось в рассмотренных выше примерах. Однако при достаточно большом количестве испытаний это приводит к очень большим вычислениям. Таким образом, возникает необходимость разработать общий подход к решению поставленной задачи. Этот подход реализован в формуле Бернулли.

Пусть в результате п независимых испытаний, проведенных в одинаковых условиях, событие А наступает с вероятностью 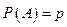, а противоположное ему событие 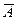с вероятностью

Обозначим 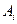– наступление события А в испытании с номером i. Так как условия проведения опытов одинаковые, то эти вероятности равны.

Если в результате п опытов событие А наступает ровно т раз, то остальные раз это событие не наступает. Событие А может появиться т раз в п испытаниях в различных комбинациях, число которых равно количеству сочетаний из п элементов по т. Это количество сочетаний находится по формуле:

.

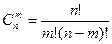Вероятность каждой комбинации равна произведению вероятностей:

.

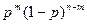Применяя теорему сложения вероятностей несовместных событий, получаем формулу Бернулли:

.

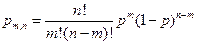Формула Бернулли справедлива для любого количества независимых испытаний, т.е. в случае, в котором наиболее четко проявляются законы теории вероятностей.

Пример. В партии 10% нестандартных деталей. Наугад отобраны 4 детали. Написать биноминальный закон распределения дискретной случайной величины Х – числа нестандартных деталей среди четырех отобранных и построить многоугольник полученного распределения.

Вероятность появления нестандартной детали в каждом случае равна 0,1.

Найдем вероятности того, что среди отобранных деталей:

1) Вообще нет нестандартных:

.

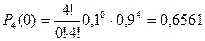2) Одна нестандартная:

.

3) Две нестандартные детали:

.

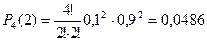4) Три нестандартные детали:

.

5) Четыре нестандартных детали:

.

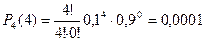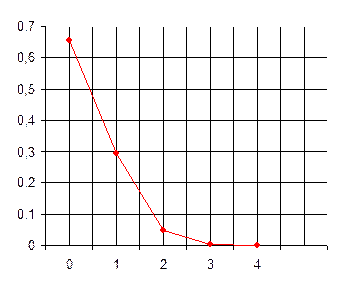Построим многоугольник распределения.

Пример. Две игральные кости одновременно бросают 2 раза. Написать биноминальный закон распределения дискретной случайной величины Х – числа выпадений четного числа очков на двух игральных костях.

Каждая игральная кость имеет три варианта четных очков – 2, 4 и 6 из шести возможных, таким образом, вероятность выпадения четного числа очков на одной кости равна 0,5.

Вероятность одновременного выпадения четных очков на двух костях равна 0,25.

Вероятность того, что при двух испытаниях оба раза выпали четные очки на обеих костях, равна:

.

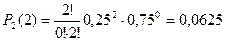Вероятность того, что при двух испытаниях один раз выпали четные очки на обеих костях:

.

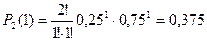Вероятность того, что при двух испытаниях ни одного раза не выпаде четного числа очков на обеих костях:

.

Пример. По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела равна 0,4. Найти вероятность того, что в цель попали не менее трех раз.

Вероятность не менее трех попаданий складывается из вероятности пяти попаданий, четырех попаданий и трех попаданий.

В случае пяти попаданий из пяти возможных:

.

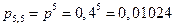Четыре попадания из пяти выстрелов:

.

Три попадания из пяти:

.

Окончательно, получаем вероятность не менее трех попаданий из пяти выстрелов:

.

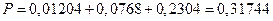Пример. Имеется шесть потребителей электрического тока, для первого из которых при определённых условиях вероятность того, что произойдёт авария, приводящая к отключению потребителя, равна 0,6, для второго - 0,2, а для четырёх остальных - по 0,3. Определить вероятность того, что генератор тока будет отключён полностью: а) если все потребители соединены последовательно; б) если потребители соединены так, как показано на схеме:

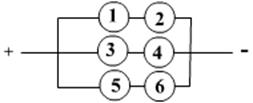
а) Вероятность не отключения всех шести потребителей равна произведению вероятностей не отключения каждого потребителя, т.е.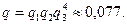

Искомая вероятность равна вероятности отключения хотя бы одного потребителя, т.е.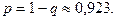

б) В этом случае генератор будет отключен полностью, если в каждой паре последовательно соединенных потребителей отключен хотя бы один потребитель:

Пример. Оптовая база снабжает 10 магазинов, от каждого из которых может поступить заявка на очередной день с вероятностью 0,4 независимо от заявок других магазинов. Найти наивероятнейшее число заявок в день и вероятность получения числа этих заявок.

В данном случае 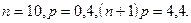Наивероятнейшее число 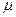заявок равно целой части числа 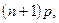т.е.

Вероятность четырех заявок из десяти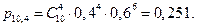

7. Распределение Пуассона дискретной случайной величины

Пусть производится п независимых испытаний, в каждом из которых появление события А происходит с вероятность р. Пусть число испытаний п достаточно велико, а вероятность появления события А в каждом испытании достаточно мало 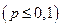. Найдём вероятность вероятности появления события А k раз. Предположим, что произведение сохраняет постоянное значение:

.

Практически это допущение означает, что среднее число появления события в различных сериях испытаний (при разном п) остается неизменным.

По формуле Бернулли находим:

;

.

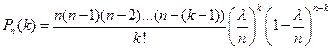Найдем предел этой вероятности при :

Получаем формулу распределения Пуассона:

.

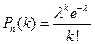Если известны числа 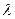и k, то значения вероятности можно найти по соответствующим таблицам распределения Пуассона.