Свойства неопределенного интеграла.

Пример 7.1.

Функция F(x)= x²является первообразной для функции f(x)= 2x на всей числовой оси, так для любого x выполняется . Функция F₁(x)= x²–3 также первообразная для f(x)= 2x, т. к. .

Функция F(x)= sinx является первообразной для f(x)= cosx, т. к. . Но функция F₁(x)= sinx + 5 также является первообразной для f(x)= cosx, т. к. .

Из примеров видно, что если задана функция f(x) , то ее первообразная не может быть определена однозначно, т. е. f(x) имеет не одну первообразную.

Теорема. Пусть функция F(x) является первообразной для f(x). Тогда и функция

F(x)+ C,

в которой С — постоянная величина, также является первообразной для f(x).

Обратно, если F₁(x) и F₂(x) — две различные первообразные для f(x), то они отличаются на постоянную величину С, т. е.

F₁(x) = F₂(x) + C.

Доказательство:

а) так как

,

то по определению первообразной функции F(x) + C является первообразной для f(x);

б) пусть у функции f(x) существуют две первообразные F₁(x)и F₂(x). Найдем их разность, которая тоже является функцией

Ф(x) = F₁(x) – F₂(x).

Найдем ее производную.

.

Так как производная функции Ф(х) равна нулю, то Ф(х) представляет собой некоторую постоянную величину С. Поэтому

Ф(х) = С, F₁(x) – F₂(x) = C F₁(x) = F₂(x) + C.

Совокупностьвсех первообразных для функции f(x) называется неопределенным интегралом от f(x) в области определения первообразных.

Неопределенный интеграл обозначается

,

где — знак интеграла, f(x) — подынтегральная функция, f(x) dx — подынтегральное выражение, а переменная x называется переменной интегрирования.

Так как все первообразные для f (x) отличаются друг от друга на постоянную величину, то ясно, что

,

т. е. неопределенный интеграл определяет семейство функций.

Процесс нахождения неопределенного интеграла от функции f(x) называется интегрированием этой функции.

Для нахождения конкретной первообразной необходимо задать координаты точки, через которую будет проходить график первообразной.

Свойства неопределенного интеграла.

1. Производная от неопределенного интеграла равна подынтегральной функции

.

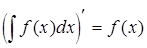Действительно,

.

2. Дифференциал от неопределенного интеграла равен подынтегральному выражению

.

По определению дифференциала

.

3. Неопределенный интеграл от дифференциала функции равен этой функции плюс произвольная постоянная

.

Так как было определено, что , то

.

4. Постоянный множитель можно вынести за знак интеграла

.

Доказательство:

.

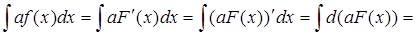
5. Интеграл от алгебраической суммы конечного числа функций равен соответствующей алгебраической сумме интегралов от этих функций

.

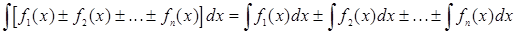Рассмотрим интегралы от основных элементарных функций в виде таблицы, которая получается путем простого подбора первообразной так, чтобы производная первообразной была бы равна подынтегральной функции.

Таблица неопределенных интегралов

1. , ;

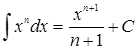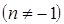2.

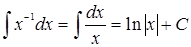
3. ;

4. ;

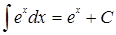5. ;

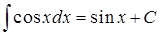6. ;

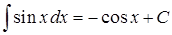7. ;

8. ;

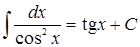9. ;

10. ;

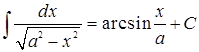11. ;

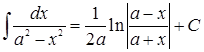12. ;

13. .

Интегралы, входящие в эту таблицу, обычно называют табличными.

Пример 7.2.

1. .

2. .

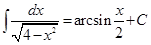3. .

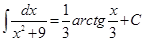4. .

5. .

Нахождение неопределенных интегралов путем обращения к таблице интегралов часто называют непосредственным интегрированием.