Глава 7 Вынужденные электрические колебания

§1 Переменный ток

Вынужденные электрические колебания в физике называют переменным током. Подобно вынужденным механическим колебаниям для получения вынужденных электрических колебаний необходимо, чтобы на колебательную систему действовала внешняя периодически меняющаяся сила. Роль внешней периодической силы теперь будет играть переменная ЭДС. Сила тока в цепи переменного тока зависит от характера переменной ЭДС. Мы рассмотрим вынужденные колебания под действием ЭДС, изменяющейся по гармоническому закону. Причина обращения именно к синусоидальной ЭДС заключается в том, что любую периодическую функцию можно разложить в ряд синусоидальных функций различных частот (ряд Фурье) и, следовательно, рассмотрение синусоидальных токов позволит в дальнейшем перейти к изучению более сложных периодических ЭДС, токов и напряжений.

Получение синусоидальной ЭДС

Принцип получения синусоидальной ЭДС промышленной частоты основан на вращении рамки в постоянном магнитном поле.

Поместим металлическую рамку в магнитное поле так, чтобы ее ось вращения была перпендикулярна магнитным линиям. Будем вращать рамку с постоянной угловой скоростью ω.

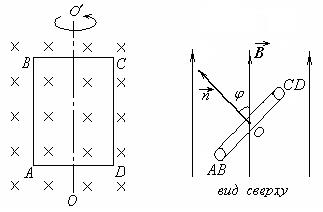
Нетрудно видеть, что угол между вектором магнитной индукции и нормалью к рамке будет изменяться

Магнитный поток, пронизывающий рамку, тоже будет изменяться

Изменение магнитного потока, как известно, приводит к возникновению в контуре ЭДС индукции. По Закону Фарадея ее можно рассчитать

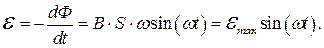(1)

Изменение ЭДС со временем представлено на рисунке:

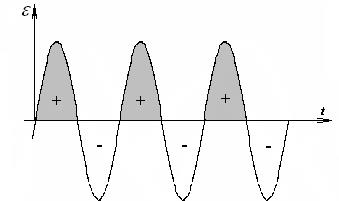
ЭДС дважды за период изменяет знак – это означает изменение полярности ЭДС, возникающей в рамке. Природа ЭДС индукции, возникающей в этом случае, - действие силы Лоренца на заряды в движущихся сторонах рамки АВ и СD.

Максимальное значение ЭДС определяется величиной индукции магнитного поля, площадью рамки и угловой скоростью ее вращения .

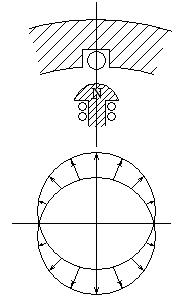На практике чаще всего вращают не рамку, а магнитное поле, индукция которого распределена внутри машины по закону косинуса .

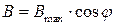Близкое к такому распределению индукции можно получить специальной формой полюсных наконечников магнита.

На вращающейся части машины – роторе – наложена обмотка возбуждения, питаемая от источника постоянного тока. Этот ток создает магнитное поле нужной конфигурации.

Обмотка, в которой генерируется переменная ЭДС, расположена в пазах неподвижной части машины – статора.

Как видно из выражения (1), циклическая частота ω синусоидальной ЭДС, возникающей в рамке, численно равна угловой скорости вращения рамки. Выразим угловую скорость вращения рамки через частоту 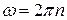и циклическую частоту переменной ЭДС через обычную частоту 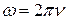. Очевидно, что частота переменной ЭДС ν совпадает с частотой вращения рам-

ки n:

.

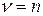Промышленная частота в России составляет v = 50 Гц. Для получения синусоидальной ЭДС такой частоты рамку необходимо вращать с частотой 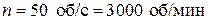. С такой частотой ротор генератора может вращать только паровая турбина. Частоту вращения ротора можно уменьшить, увеличив число пар полюсов электромагнита: 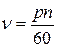, где р – число пар полюсов,

n – частота вращения ротора ( число оборотов в минуту). Например, частота вращения генераторов на Днепровской ГЭС об/мин. Для получения промышленной частоты 50 Гц генераторы ГЭС имеют р = 36 пар полюсов.

Квазистационарные токи

При рассмотрении электрических колебаний приходится иметь дело с токами, изменяющимися со временем. Законы постоянного тока оказываются справедливыми и для изменяющихся (переменных) токов, если только изменение силы тока происходит не слишком быстро. Если изменения тока настолько медленны, что за время установления электрического равновесия в цепи относительные изменения токов и ЭДС малы, то мгновенные значения токов и ЭДС будут подчиняться всем законам постоянного тока. Такие токи называют медленно меняющимися или квазистационарными. Для квазистационарного тока мгновенные значения тока оказывается практически одинаковыми на всех участках цепи.

Мощность в цепи переменного тока

Мы знаем, что под действием периодически изменяющейся внешней силы механическая колебательная система будет совершать колебания с частотой этой вынуждающей силы. Электрическая система откликается на наличие переменной ЭДС в цепи аналогично – в ней возникает переменный ток, изменяющийся с частотой переменной ЭДС, генерируемой источником. В общем случае, между током в каком-либо участке цепи и напряжением на его концах будет наблюдаться сдвиг по фазе. Этот сдвиг по фазе зависит от параметров цепи и частоты переменной ЭДС.

В цепи переменного тока происходит преобразование электрической энергии в другие виды энергии: тепловую (лампа накаливания, электроплитка, утюг и т.д.) и механическую (электрический двигатель). Для характеристики быстроты преобразования электрической энергии в другие виды энергии вводят мощность.

Мгновенной мощностью называют произведение мгновенных значений тока и напряжения (как для цепи постоянного тока):

Легко видеть, что численное значение мгновенной мощности в цепи переменного тока непрерывно меняется, более того, может меняться и знак этой величины. Этот факт не позволяет использовать мгновенную мощность для расчета энергии, потребляемой цепью за большой интервал времени. Тем не менее, понятие мгновенной мощности чрезвычайно важно хотя бы потому, что знак этой величины позволяет ответить на вопрос: потребляет цепь энергию от источника в данный момент времени или отдает. Если мгновенная мощность положительна, цепь потребляет энергию от источника; мгновенная мощность отрицательная – цепь отдает энергию источнику.

С другой стороны, понятно, что энергетический баланс между источником тока и потребителем за каждый период одинаков. Этот факт позволяет ввести понятие средней за период мощности.

За малый интервал времени 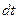изменением тока и напряжения можно пренебречь, и работу тока за этот малый интервал времени (именно она является мерой преобразования электрической энергии в другие виды энергии) рассчитать как для цепи постоянного тока

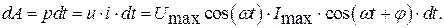
Работа тока за период может быть найдена суммированием малых работ за время, равное периоду

Тогда средняя за период мощность может быть найдена как

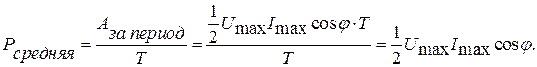
Видим, что средняя за период мощность в цепи переменного тока зависит не только от максимальных значений тока и напряжения, но и от сдвига по фазе φ между током и напряжение. Множитель называют коэффициентом мощности. Чем больше коэффициент мощности, тем более полно энергия источника преобразуется в необходимые нам виды энергии. Величина сдвига по фазе между током и напряжением определяется характером нагрузки в цепи.

В цепях переменного тока различают три вида нагрузок: активная, индуктивная, емкостная. Рассмотрим каждый вид нагрузки по отдельности. Главный вопрос, который предстоит решить – разрешено ли применение закона Ома для расчета цепи, содержащей данный вид нагрузки.

Активная нагрузка в цепи переменного тока

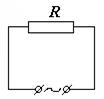Активной нагрузкой в цепи переменного тока называется такой участок, на котором вся электрическая энергия необратимо преобразуется в тепловую. В роли активной нагрузки может быть обычный резистор (лампа накаливания, электронагревательный элемент и т.д.)

Пусть напряжение на концах участка цепи, являющегося активной нагрузкой, меняется по гармоническому закону .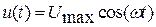

Чтобы вся электрическая энергия необратимо преобразовывалась в тепловую энергию, необходимо, чтобы мгновенная мощность в любой момент времени была положительной, а это возможно только при 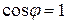. Следовательно, для активной нагрузки напряжение и сила тока колеблются в одной фазе.

Нетрудно видеть, что мгновенные значения силы тока 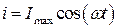и напряжения пропорциональны друг другу. Это утверждение – не что иное, как закон Ома для участка цепи:

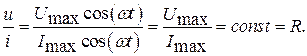
Таким образом, на активной нагрузке закон Ома выполняется как для мгновенных, так и для амплитудных значений.

При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться амплитудными или мгновенными значениями токов и напряжений, а их средние значения за период равны нулю.

Наиболее удобным оказалось введение так называемых действующих значений тока и напряжения. В основу этих понятий положено тепловое действие тока.

Действующее значение переменного тока – это значение постоянного тока, при протекании которого по цепи в проводнике выделяется за период столько же теплоты, сколько и при протекании переменного тока.

Тепло, выделяемое в резисторе при протекании по нему постоянного тока, может быть найдено из закона Джоуля –Ленца:

(*)

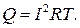Тепло 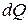, выделяемое переменным током в том же сопротивлении R за малое время 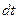, может быть выражено через мгновенное значение тока :

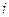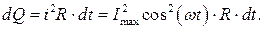
Тепло, выделяемое за период, находим суммированием малых :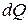

(**)

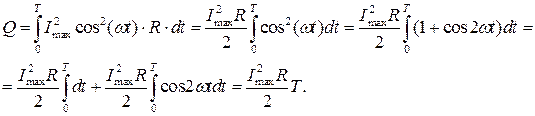Приравняв (*) и (**), найдем действующее значение переменного тока:

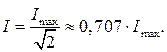
Выражения для действующих значений ЭДС и напряжения выглядят аналогично:

В соответствии с ГОСТом действующие значения тока, напряжения и ЭДС обозначаются соответствующими прописными буквами без индексов.

Электроизмерительные приборы переменного тока градуируют в действующих значениях измеряемых величин.

5 Емкостная нагрузка в цепи переменного тока

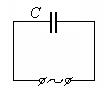Конденсатор в цепи переменного тока представляет так называемую емкостную нагрузку. Наличие диэлектрика между обкладками конденсатора приводит к тому, что постоянный ток не может течь по участку цепи, содержащему конденсатор. В цепи переменного тока ситуация меняется: под действием переменной ЭДС конденсатор может заряжаться и разряжаться, в этом случае по участку цепи, содержащему конденсатор, протекает ток зарядки или разрядки.

Наша задача – выяснить, как меняется ток зарядки и разрядки конденсатора, если его подключить к источнику синусоидальной ЭДС .

Очевидно, что напряжение на конденсаторе совпадает с напряжением на клеммах генератора 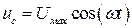. Тогда заряд на конденсаторе

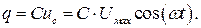
Поскольку ток зарядки конденсатора – не что иное, как производная от заряда на конденсаторе по времени, получаем:

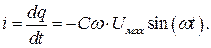
Воспользуемся формулами приведения:

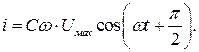
Видим, что ток в цепи, содержащей конденсатор, меняется по гармоническому закону с частотой переменной ЭДС. Однако, фазы напряжения на конденсаторе и тока отличаются. Ток опережает напряжение на конденсаторе на .

Сравнивая графики зависимостей тока и напряжения от времени, нетрудно увидеть, что пропорциональность между мгновенными значениями тока и напряжения отсутствует. Иными словами, закон Ома для мгновенных значений тока и напряжения не выполняется!

Вернемся к зависимости тока от времени

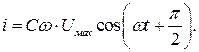
Величина, стоящая перед знаком косинуса, - амплитудное значение тока

Максимальное значение тока в цепи с конденсатором прямо пропорционально максимальному значению напряжения. Это означает, что для амплитудных значений тока и напряжения выполняется закон Ома.

Коэффициент пропорциональности 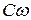- проводимость участка цепи, содержащего конденсатор. Тогда величина играет роль сопротивления, его называют емкостным сопротивлением.

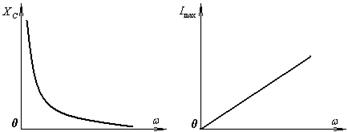
Емкостное сопротивление зависит не только от емкости конденсатора, но и от частоты тока 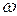.С увеличением частоты тока сопротивление конденсатора падает, а амплитуда тока при этом, наоборот, увеличивается. Таким образом, конденсатор хорошо «пропускает» ток высокой частоты и плохо – низкой. Сопротивление конденсатора становится бесконечно большим, если частота тока 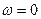, то есть постоянный ток не может течь через участок, содержащий конденсатор (как это уже было сказано ранее).

Коэффициент мощности для участка цепи, содержащего конденсатор, равен нулю 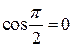, следовательно, участок цепи, содержащий конденсатор, не потребляет энергию от сети. Точнее, мгновенная мощность в цепи с конденсатором меняет знак через каждые четверть периода. Четверть периода конденсатор заряжается, потребляя энергию от источника, на этом этапе мгновенная мощность положительна. Следующую четверть периода конденсатор разряжается, возвращая энергию источнику, при этом мгновенная мощность отрицательна.

Роль емкостного сопротивления, таким образом, сводится к ограничению силы тока в цепи, содержащей конденсатор.

6 Индуктивная нагрузка в цепи переменного тока

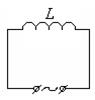Рассмотрим поведение идеальной катушки индуктивности, если ее подключить к источнику синусоидальной ЭДС 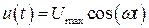. Выясним, как изменяется ток в цепи с течением времени.

Запишем второй закон Кирхгофа для рассматриваемого контура: сумма падений напряжений вдоль замкнутого контура равна сумме ЭДС, действующих вдоль этого контура.

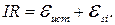
Учтем, что активное сопротивление 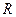идеальной катушки равно нулю. Тогда

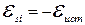
После интегрирования получаем

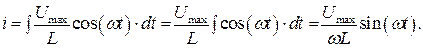
Применим формулы приведения

Видим, что по катушке индуктивности течет переменный ток, частота которого совпадает с частотой генератора. Однако, колебания тока и напряжения на катушке не совпадают по фазе – ток отстает от напряжения на .

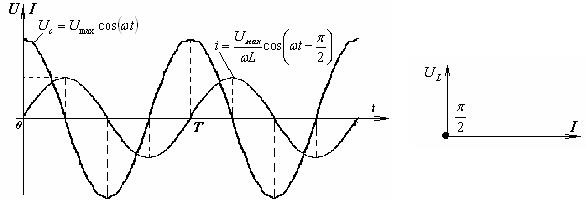
Анализ графиков зависимостей и 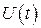показывает, что между мгновенными значениями тока и напряжения отсутствует пропорциональность. Это означает, что в цепи переменного тока, содержащей индуктивность, закон Ома для мгновенных значений тока и напряжения не выполняется.

Однако, максимальное значение тока 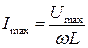прямо пропорционально амплитудному значению напряжения. Следовательно, для амплитудных значений тока и напряжения выполняется закон Ома.

Величина 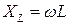играет роль сопротивления и называется индуктивным сопротивлением. Видим, что кроме индуктивности 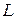сопротивление катушки зависит еще и от частоты 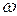протекающего по ней тока.

Сопротивление катушки растет при увеличении частоты тока. Таким образом, катушка, в отличие от конденсатора, хорошо пропускает низкочастотный ток, и плохо – высокочастотный.

Цепь, содержащая индуктивность, как и цепь с емкостной нагрузкой, не потребляет энергии от сети, ибо сдвиг по фазе между током и напряжением равен 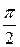. Строго говоря, четверть периода, когда ток в катушке нарастает, она потребляет энергию от источника, потребляемая от источника энергия переходит в энергию магнитного поля тока. В течение этой четверти периода мгновенная мощность положительна. Следующую четверть периода ток в катушке убывает, его магнитное поле «исчезает», энергия отдается источнику, мгновенная мощность отрицательна. Так что в целом за период на индуктивной нагрузке не происходит необратимого преобразования электрической энергии в другие виды энергии. По этой причине индуктивную и емкостную нагрузки в цепи переменного тока называют реактивной нагрузкой.

Упражнения

Емкостная нагрузка в цепи переменного тока

1 Рассчитайте сопротивление конденсатора емкостью С = 0,1 мкФ переменному току, если частота тока а) 50 Гц; б) 1000 Гц; в) 10 кГц. Постройте график зависимости емкостного сопротивления от частоты переменного тока.

2 К городской сети переменного тока с напряжением U_эф = 127 В присоединен конденсатор емкостью С = 40 мкФ. Определите амплитудное значение тока в цепи.

3 К зажимам генератора присоединен конденсатор емкостью С = 0,1 мкФ. Определите амплитуду напряжения на зажимах генератора, если амплитуда тока I_max = 2,2 А, а частота тока n = 5 кГц.

4 Найдите емкость конденсатора, если амплитуда переменного напряжения на нем U₀ =120 В, действующее значение тока I = 0,86 А, частота тока n = 50 Гц.

Индуктивная нагрузка в цепи переменного тока

1 Индуктивность катушки L = 0,5 мГн. Рассчитайте сопротивление катушки переменному току, если его частота а) 50 Гц; б) 1000 Гц; в) 10 кГц. Постройте график зависимости индуктивного сопротивления от частоты переменного тока. Катушка идеальная.

2 Найдите индуктивность катушки, если амплитуда переменного напряжения на ее концах U_мах = 160 В, амплитуда тока в ней I_мах = 10 А и частота тока 50 Гц. Катушка идеальная.

3 Индуктивное сопротивление катушки Х_L = 500 Ом, эффективное напряжение в сети, в которую включена катушка, U_эф = 100 В, частота тока 1000 Гц. Определите индуктивность катушки и амплитудное значение тока в цепи. Активным сопротивлением катушки и подводящих проводов пренебречь.

Указания:

1 Помним, что для расчета емкостного или индуктивного сопротивления необходимо знать циклическую частоту w, а не обычную частоту n. Связь между ними w = 2pn.

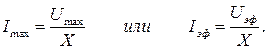2 Закон Ома для цепи с катушкой или конденсатором можно записать как для амплитудных, так и для действующих (эффективных) значений тока и напряжения.

Нельзя применять закон Ома, если значение одной из величин (тока или напряженяе) действующее, а значение другой величины амплитудное!!!

3 Действующие и амплитудные значения тока и напряжения связаны между собой следующим образом

Действующее и эффективное значение тока или напряжения – это одно и то же! Можно обозначать так, как Вам больше нравится – возможны три варианта:

§ 2 Последовательное соединение R, L, C

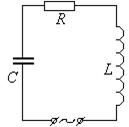Рассмотрим реальный колебательный контур с источником синусоидальной ЭДС. Задача заключается в определении тока, протекающего по цепи.

Задачу можно решить двумя способами: алгебраически и геометрически. Обратимся сначала к алгебраическому решению. Запишем для контура второй закон Кирхгофа – сумма падений напряжений вдоль замкнутого контура равна сумме ЭДС, действующих в контуре:

С учетом того, что

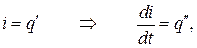
уравнение перепишется в виде

Введем привычные обозначения 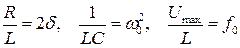. Тогда дифференциальное уравнение примет вид .

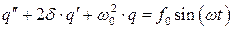С подобным дифференциальным уравнением мы уже сталкивались, рассматривая вынужденные механические колебания под действием синусоидальной внешней вынуждающей силы. Тогда же мы показывали, что решение уравнения ищется в виде .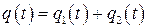

- решение однородного дифференциального уравнения имеет вид 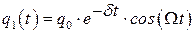, где . С физической точки зрения это означает, что включение переменного тока сопровождается «звоном» собственных колебаний контура, затухающих с течением времени. Время затухания собственных колебаний будет порядка времени релаксации .

Если же мы, как обычно в электротехнике, интересуемся установившимися колебаниями при 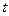>> 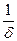, то, как было уже показано ранее решение дифференциального уравнения ищется в виде 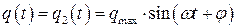. Физический смысл решения заключается в том, что под действием синусоидальной ЭДС в контуре будут происходить гармонические колебания с частотой внешней ЭДС. Очевидно, что мгновенные значения тока в контуре и напряжения на клеммах генератора сдвинуты по фазе, а это означает, что закон Ома для мгновенных значений тока и напряжения не выполняется.

В силу математической тождественности дифференциальных уравнений вынужденных механических и вынужденных электрических колебаний

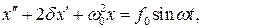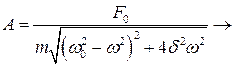мы можем воспользоваться уже готовым результатом, проведя замену механических величин на соответствующие электрические. Тогда

Ток к цепи равен 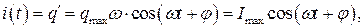где

Амплитуда тока в контуре прямо пропорциональна амплитуде напряжения, то есть для амплитудных значений тока и напряжения выполняется закон Ома.

Величина 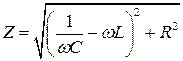играет роль сопротивления последовательной 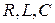- цепи. Такое «сопротивление» принято называть импедансом.

Выше найден сдвиг фаз между зарядом и напряжением , а поскольку колебания тока опережают колебания заряда на 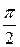, то сдвиг фаз между током и напряжением будет .

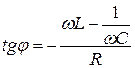Итак, поставленная задача решена. Мы показали, что под действием синусоидальной ЭДС в колебательном контуре происходят гармонические колебания тока, нашли амплитуду тока и сдвиг по фазе между током и напряжением. Для последовательной 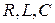- цепи можно пользоваться готовыми формулами. Однако, как правило, цепи переменного тока бывают не только последовательными. В этих случаях полученный нами результат не годится. В этих случаях гораздо проще рассчитать цепь графически, а не алгебраически. Покажем, как это делается.

При последовательном соединении сила тока одинакова во всех участках цепи, следовательно, 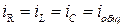. Если 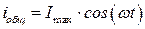, то колебания напряжения на активной нагрузке 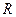совпадают по фазе с колебания ми силы тока .

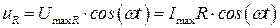На емкостной нагрузке колебания напряжения отстают от тока на : .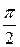

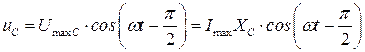На индуктивной нагрузке напряжение опережает ток на : .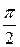

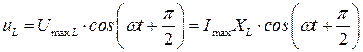Мгновенное значение общего напряжения при последовательном соединении равно сумме напряжений на отдельных участках

Для сложения гармонических функций одинаковой частоты удобно воспользоваться методом векторных диаграмм. Каждое колебание изображается вектором, которому в полярных координатах соответствуют модуль (амплитуда) и полярный угол (фаза).

Изобразим вектор тока горизонтально. Напряжение на активной нагрузке синфазно току, соответственно откладываем вектор 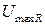параллельно вектору тока. Напряжение 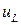опережает ток на 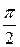, соответственно откладываем вектор перпендикулярно току с опережением по фазе. Напряжение 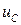отстает от тока на 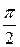, откладываем вектор 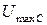перпендикулярно току с отставанием по фазе.

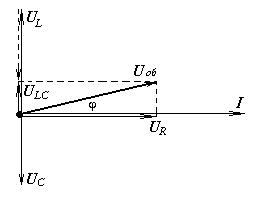
На диаграмме, как правило, опускают индексы «max», чтобы не загромождать рисунок.

Сумма всех трех векторов напряжений даст вектор общего напряжения . Нетрудно видеть, что между током и напряжением существует сдвиг по фазе, это значит, что между мгновенными значениями тока и напряжения пропорциональность отсутствует. Для мгновенных значений тока и напряжения закон Ома не выполняется!

Сдвиг по фазе между напряжением и током

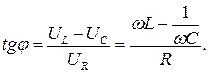
Амплитуда общего напряжения 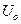равна

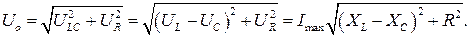
Опять-таки обнаруживаем пропорциональность между амплитудными значениями тока и напряжения, это значит, что для них выполняется закон Ома.

Резонанс напряжений (резонанс в последовательной -цепи)

Предположим, что при заданной амплитуде напряжения на клеммах генератора мы будем варьировать частоту 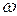внешней ЭДС. Очевидно, что амплитуда силы тока будет меняться, ибо индуктивное 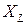и емкостное 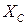сопротивления зависят от частоты .

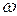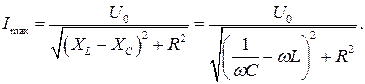
Нетрудно видеть, что амплитуда тока примет максимальное значение при услови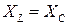и или . В этом случае наблюдается резонанс. При последовательном соединении элементов он называется резонансом напряжений. Векторная диаграмма при резонансе выглядит следующим образом.

Напряжения на индуктивном и емкостном сопротивлениях равны по модулю и колеблются в противофазе, следовательно, они компенсируют друг друга. Общее напряжение становится равным падению напряжения на активной нагрузке.

Часто параметры контура подбираются таким образом, что 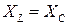>> 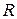. Тогда >> . При резонансе напряжений напряжения на отдельных участках цепи (на емкости и индуктивности) могут значительно превосходить напряжение на клеммах генератора.

Сдвиг по фазе между током и общим напряжением при резонансе обращается в ноль. При резонансе колебательный контур ведет себя как цепь исключительно с активной нагрузкой.

Частота тока, при которой наблюдается резонанс, может быть найдена следующим образом:

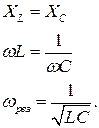
Как и следовало ожидать, резонанс наблюдается при совпадении частоты генератора с собственной частотой колебательного контура.

Резонансная кривая выглядит следующим образом

§ 3 Резонанс токов

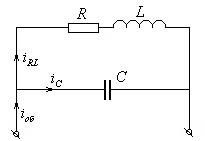Рассмотрим параллельное соединение конденсатора с катушкой. Поскольку реальная катушка обладает активным сопротивлением, эквивалентная электрическая цепь будет выглядеть следующим образом:

Задача остается прежней – зная приложенное напряжение, рассчитать ток в цепи.

При параллельном соединении напряжения на ветвях, содержащих конденсатор и катушку, одинаковые . Ток в неразветвленной части 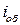(его мы и хотим определить) делится на два тока .

Для расчета этой цепи удобнее воспользоваться методом векторных диаграмм.

Начнем с ветви, содержащей индуктивность и активное сопротивление.

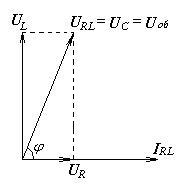
Напряжение на активной нагрузке совпадает по фазе с током – на векторной диаграмме вектор сонаправлен вектору .

Напряжение на индуктивной нагрузке опережает ток на 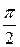- строим вектор перпендикулярно вектору тока с опережением по фазе. Общее напряжение находим по правилу параллелограмма. Оно опережает ток в 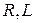-ветви на 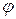радиан.

Сопротивление 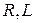- ветви равно 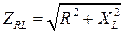. Амплитуда тока в этой ветви может быть найдена по закону Ома 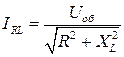, а сдвиг по фазе 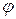определим по чертежу .

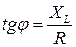Разложим ток в 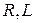- ветви на две составляющих – активную 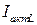, параллельную вектору напряжения, и 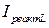, перпендикулярную вектору напряжения:

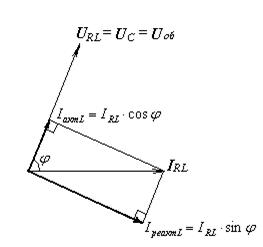
Теперь перейдем к построению векторной диаграммы для всей цепи. Поскольку напряжение на отдельных ветвях одинаково, в основу диаграммы положим вектор общего напряжения 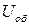, расположив его горизонтально.

Ток в ветви, содержащей емкость, найдем по закону Ома . Этот ток опережает напряжение по фазе на 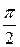и колеблется в противофазе с 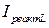. Ток в неразветвленной части цепи может быть найден по теореме Пифагора:

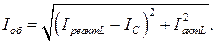
Нетрудно видеть, что при выполнении условия ток в неразветвленной части цепи принимает минимальное значение, равное 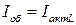. При этом токи в ветвях 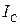и могут оказаться намного больше тока в неразветвленной части цепи, при этом они колеблются практически в противофазе. В этом случае мы имеем дело с так называемым резонансом токов. Векторная диаграмма для резонанса токов выглядит следующим образом: