Прогнозирование случайных процессов
Прогнозирование случайных процессов использует статистические характеристики процессов, такие как математическое ожидание M[X(t)] и ковариационная функция RX(t). Особое значение имеет время, в течение которого между сечениями случайного процесса сохраняется статистическая связь – t0.
Иногда t0 – это половина ширины основания прямоугольника единичной высоты, площадь которого равна площади под кривой модуля rX(t) – корреляционной функции случайного процесса:
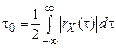 . (5.43)
. (5.43)
Если t0 = 0, то процесс представляет собой «белый шум».
Для тепловой электростанции можно оценить время t0 некоторых процессов:
· флуктуация яркости факела в топке – доли секунды;
· температура перегретого пара – минуты;
· нагрузка генератора и расход топлива – десятки минут;
· теплотворная способность твердого топлива – десятки суток.
Время t0 называют еще интервалом корреляции процесса.
Ошибка прогноза есть разница действительного и прогнозного значений процесса:
 . (5.44)
. (5.44)
Дисперсия ошибки прогноза может быть получена как математическое ожидание квадрата ошибки процесса, так как математическое ожидание стационарного случайного процесса неизменно во времени:
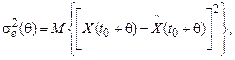 (5.45)
(5.45)
где t0 – момент времени, в который выполняется прогноз;
q – время упреждения;
X(t0 + q) – истинное значение процесса на момент прогноза;
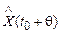 - прогнозное значение.
- прогнозное значение.
Существует три основных метода прогнозирования случайного процесса:
· по последнему значению,
· по математическому ожиданию,
· по условному математическому ожиданию (статистический прогноз).
Прогноз по последнему значению
Прогнозное значение принимается равным последнему значению
 (5.46)
(5.46)
Ошибка прогноза
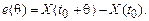 (5.47)
(5.47)
Дисперсия ошибки

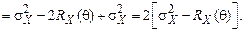 (5.48)
(5.48)
Дисперсия ошибки растет от 0 при θ = 0 до удвоенной дисперсии процесса при θ → ∞, но на отдельных, близких к начальному моменту времени интервалах, может превышать удвоенную дисперсию процесса, что объясняется возможной отрицательной корреляцией сечений процесса.
Прогноз по математическому ожиданию
Прогнозное значение принимается равным математическому ожиданию процесса
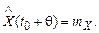 (5.49)
(5.49)
Ошибка прогноза равна
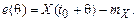 (5.50)
(5.50)
Дисперсия ошибки
 . (5.51)
. (5.51)
Статистический прогноз
В качестве прогнозного значения берется условное математическое ожидание процесса в сечении на момент времени t0 + θ.
Обозначим случайный процесс в сечении на момент времени t0 через X, а в момент времени t0 + θ через Y и рассмотрим их как систему двух случайных величин (X,Y). Таким образом,
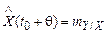 . (5.52)
. (5.52)
Ошибка прогноза
 (5.53)
(5.53)
Дисперсия ошибки есть условная дисперсия случайной величины Y:
 . (5.54)
. (5.54)
Условное математическое ожидание случайной величины Y:
 , (5.55)
, (5.55)
где rX,Y – коэффициент корреляции между случайными величинами X и Y;
mX и mY – безусловные математические ожидания случайных величин X и Y;
σX и σY – среднеквадратические отклонения случайных величин X и Y.
Таким образом, с учетом mX = mY = m и sX = sY = s имеем прогнозное значение
 (5.56)
(5.56)
и дисперсию ошибки прогноза
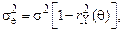 (5.57)
(5.57)
где s = sX – среднеквадратическое отклонение процесса.
Сопоставление методов прогноза
Сравнивая методы прогноза, можно сделать следующие заключения.
· Прогнозное значение не зависит от времени упреждения для первого и второго методов.
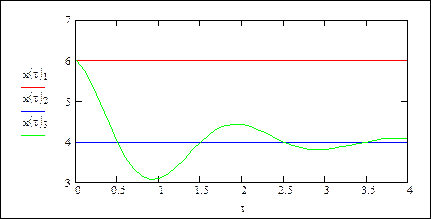
· Ошибка прогноза в методе по последнему значению в сильной мере зависит от времени упреждения. При малом θ дисперсия ошибки невелика (рис. 5.16, кривая 1), но с ростом θ стремится к удвоенному значению дисперсии процесса и при отрицательной корреляции между сечениями процесс может превышать удвоенное значение дисперсии процесса. Поэтому первый метод хорошо использовать для прогнозирования на малые периоды времени.
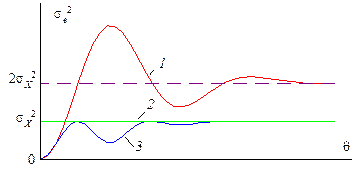
Рис. 5.16. Погрешности трех методов прогноза
· Третий, статистический, метод при малом времени упреждения приближается к методу по последнему значению (рис. 5.16, кривая 3), а с ростом θ имеет наименьшую погрешность из всех рассмотренных методов. С ослаблением статистической связи между сечениями процесса ошибка статистического прогноза приближается к ошибке метода по математическому ожиданию (рис. 5.16, кривая 2). Поэтому для краткосрочного и долгосрочного прогноза случайная составляющая процесса никак не влияет на прогноз.
Пример 2. Вычислить значение стационарного случайного процесса через 3 с после регистрации последнего значения, если известно значение процесса на момент регистрации (текущее значение) и его характеристики: математическое ожидание, дисперсия и ковариационная функция, заданная аналитическим выражением  . Для прогноза использовать все три метода: по последнему значению, по математическому ожиданию и статистический метод.
. Для прогноза использовать все три метода: по последнему значению, по математическому ожиданию и статистический метод.
Расчеты выполним в системе Mathcad.
Исходные данные

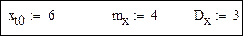
вычисления
Определение функций прогноза и прогнозные значения по всем трем методам:
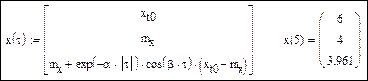
Графики функций прогноза:
Функции дисперсий ошибок прогноза по трем методам и значения дисперсий ошибок со временем упреждения 3 с:

