Метод кусочно-линейной аппроксимации

Этот метод удобно использовать для некоторых задач специального вида, а именно в случае, когда целевая функция (4.5) и ограничивающие функции из (4.6) являются сепарабельными. Напомним, что функция 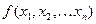называется сепарабельной, если её можно представить в виде суммы функций, зависящих только от одной переменной: .

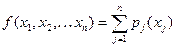Пусть дана задача:

(4.11)

на множестве допустимых решений, заданных ограничениями:

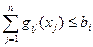, (4.12)

. (4.13)

Такую задачу можно свести к ЗЛП. Для этого:

- определяем максимально возможные значения 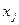(чаще всего по соображениям здравого смысла), т.е. полагаем, что ;

- разбиваем интервал 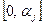на 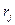равных промежутков длины точками: 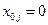, , ..., ,...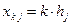., . где .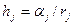

Очевидно, можно записать

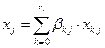(4.14)

получаем естественные ограничения

для ; (4.15)

- заменяем 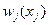кусочно-линейной аппроксимацией, т.е. представляем в виде

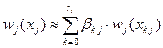; (4.16)

- также обходимся с ограничивающими функциями 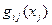, представив их в виде

. (4.17)

Учитывая, что значения 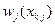, 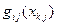известны при любых 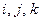, подставляем (4.14-4.16) в (4.11-4.13) и получаем задачу линейного программирования с неизвестными .

Решение исходной задачи получим, найдя искомые значения 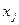по (4.14) и вычислив по (4.11) оптимум целевой функции. Точность решения зависит от принятых шагов разбиения. Чем мельче шаги, тем точнее решение.

Пример:

Найти максимум целевой функции:

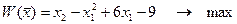
при условиях:

.

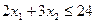
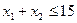
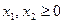Решение:

В целевой функции

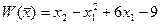
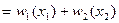
нелинейным является только первое слагаемое , второе слагаемое 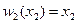линейно.

Из вида области допустимых решений следует, что 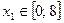. Разбиваем этот промежуток на 8 частей точками:

и вычисляем в этих точках значения :

,

, .

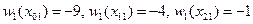По (4.14), (4.16) находим:

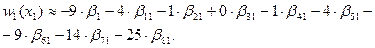
В итоге получаем задачу линейного программирования:

Найти максимум целевой функции с десятью неизвестными

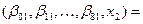
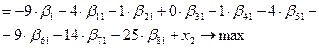
при условиях:

,

,

,

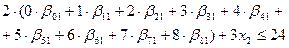
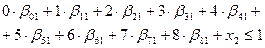
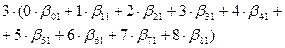
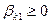Решив линейную задачу, найдем, что достигает максимума при

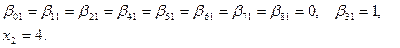Переходя к исходной нелинейной задаче, получаем

Ответ:

,

.

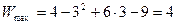Глава 5. Принятие решений в условиях

Неполной информации

При принятии решений в условиях неполной информации, большая ответственность ложится на лицо принимающее решение (ЛПР), так как окончательный выбор оптимального решения на основе поставленной цели зависит от точки зрения ЛПР.

Принятию решения обычно предшествует количественный анализ, при котором определяются возможные варианты решения проблемы, возможные исходы каждого решения и их оценка.

Критерии принятия решений в рассматриваемых задачах делятся на две группы:

- без использования численных значений вероятностей исходов, то есть в условиях стохастической неопределенности;

- с использованием численных значений вероятностей исходов, когда параметры модели считаются случайными величинами с известными законами распределения, то есть в условиях риска.

Такие задачи относят к теории игр и называют также играми с природой, где один игрок — лицо принимающее решение, а второй — внешние факторы или обстоятельства, к которым можно отнести и погоду.