Передаточные функции разомкнутой и замкнутой САР
1) Передаточная функция оптимального разомкнутого контура имеет вид:
Подставляя данные, получим:
Передаточная функция оптимального замкнутого контура имеет вид:
Подставляя данные, получим:
2) Тр1 = 0,5 Т01 = 0,0375 <Тр1опт; 
.
Передаточная функция разомкнутого контура имеет вид:
Подставляя данные, получим:
Передаточная функция замкнутого контура имеет вид:
Подставляя данные, получим:
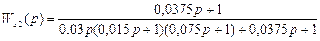
3) Тр1 = 2Т01 = 0,15 > Тр1опт; 
.
Передаточная функция разомкнутого контура имеет вид:
Подставляя данные, получим:
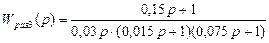
Передаточная функция замкнутого контура имеет вид:
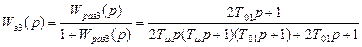
Подставляя данные, получим:
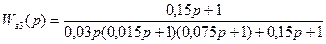
2.6.1.2 Расчет и построение логарифмических частотных характеристик замкнутого и разомкнутого внутреннего контура САР
Первый случай.
Разомкнутая:
Замкнутая:
Второй случай:
Разомкнутая:
Разомкнутая САР представляет собой последовательно соединенные два апериодических, интегральное и дифференцирующее звенья.
Замкнутая:
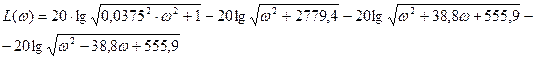
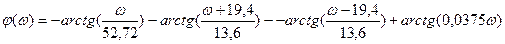
Для третьего случая:
Разомкнутая:
Замкнутая:
2.6.2 Построение ЛАЧХ и ЛФЧХ при изменении постоянной времени Тр1.
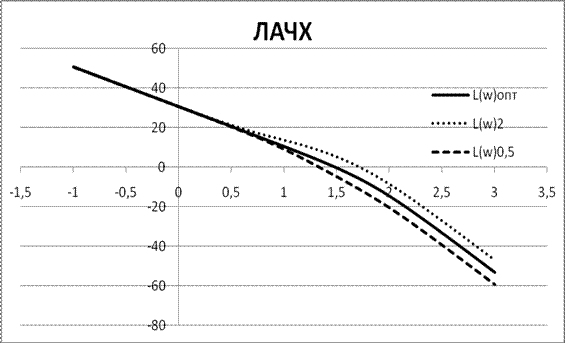
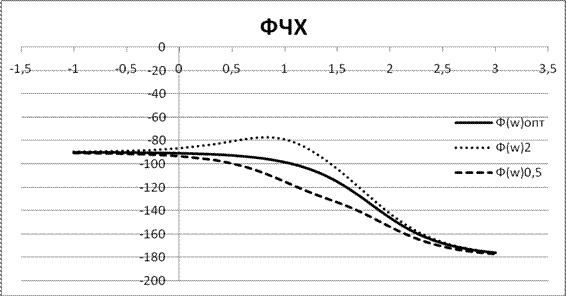
Рисунок 2.5 Логарифмические частотные характеристики разомкнутой САР
Рисунок 2.6. Логарифмические частотные характеристики замкнутой САР
Выводы: в результате исследования выяснилось:
При изменении постоянной Tр1 система перестает быть оптимальной. Изменение Tр1 ведет к усложнению передаточной функции как замкнутой, так и разомкнутой САР. Оптимальность системы при этом нарушается. Новые передаточные функции состоят из четырех последовательно соединенных звеньев.
При изменении постоянной Tр система перестает быть оптимальной. Увеличение Tр в два раза ведет к увеличению коэффициента затухания в корень из двух раз, а уменьшение Tр – к уменьшению ξ в той же пропорции. Следовательно при увеличении Tр звено становится более инерционным, а при уменьшении – более колебательным, что приводит к увеличению времени регулирования и увеличению перерегулирования (для более колебательного звена).
2.6.1.3 Расчет переходных процессов по методу моделирования на компьютере.
С помощью программы автоматического моделирования MATLAB произведем моделирование. Для этого используем файл SIMULINK (смотри рисунок 2.7)
Рисунок 2.7 - Исследование динамических свойств внутреннего контура регулирования САР при изменении постоянной времени регулятора Tр1
1) Максимальный выброс величин y1, y2и y3:
ymax y1 = 1,043; ymax y2 =1,05; ymax y3 = 1,15.
2) Перерегулирование s %:
sу1 % = 
;
sy2 % =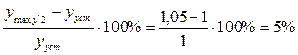 
;
sy3 % = 
.
3) относительное время регулирования 
:
а)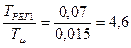 
б) 
в) 
Анализ переходных процессов, представленных на рис. 2.4. и рис. 2.7., показывает:
ü при уменьшении постоянной времени 
снижается время переходного процесса, но возрастает перерегулирование;
ü при возрастании величины снижается перерегулирование за счет увеличения времени переходного процесса;
ü уменьшение и увеличение постоянной времени 
по сравнению с оптимальным значением 
приводит к увеличению перерегулирования при уменьшении времени переходного процесса в первом случае и увеличении его во втором случае;
ü уменьшение и увеличение постоянной времени по сравнению с оптимальным значением приводит к усложнению передаточной функции как замкнутой, так и разомкнутой САР;
ü оптимальный переходный процесс обеспечивается только при оптимальной настройке регулятора, т.е. при и Тр =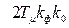 
.
3. Расчет и исследование двухконтурной статической САР с последовательной коррекцией.
3.1 Составление структурной схемы двухконтурной САР.
Рисунок 3.1 – Структурная схема двухконтурной САР.
- передаточная функция той части ОР, которая компенсируется регулятором контура;
- постоянная времени ОР звена;
- передаточная функция внутреннего замкнутого контура;
- передаточная функция регулятора внешнего контура.
На внешний контур действуют следующие воздействия:
1) g=yз2 – задающие воздействия;
2) F(p) – возмущающее воздействие, которое действует на объект управления.
Регулируются следующие параметры:
1) y1 – выходная величина внутреннего контура;
2) y2 – выходная величина внешнего контура.
Передаточная функция регулятора определиться по формуле:
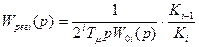
где i – номер рассматриваемого контура;
Tμ – наименьшая некомпенсируемая постоянная времени;
W0i(p) – передаточная функция той части объекта регулирования, которая должна быть скомпенсирована регулятором рассматриваемого контура.
Ki ,Ki-1 – коэффициенты обратной связи рассматриваемого и предыдущего внутреннего контура соответственно.
Рассмотрим внешний контур САР.
Передаточная функция определится:
Регулятор внешнего контура является пропорциональным звеном. Согласно этому строим схему внешнего контура САР (рисунок 3,2.).
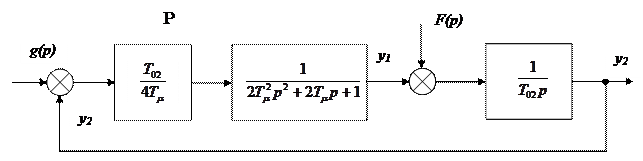
Рисунок 3.2. - Схема внешнего контура САР
Т.к. Tμ величина маленькая, то ее квадрат еще меньше, следовательно, ей можно пренебречь. При этом передаточная функция внутреннего контура упростится и станет оптимальной функцией первого порядка с постоянной времени T’μ=2Tμ=0,03с. Структурная схема внешнего контура примет вид ( рисунок 3.3).
Рисунок 3.3 - Упрощенная схема внешнего контура САР
3.2 Передаточные функции замкнутой и разомкнутой САР, по управляющему и возмущающему воздействиям.
3.2.1. Передаточные функции разомкнутой и замкнутой САР, по управляющему воздействию. Рассмотрим передаточную функцию внутреннего замкнутого контура.
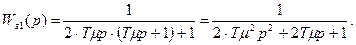
где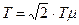 
, 
Вывод: В данном случае внутренний замкнутый контур будет представлять из себя апериодическое звено 1го порядка. Необходимо найти передаточные и переходные функции для случаев, когда внутренний замкнутый контур – колебательное звено.
3.3.1.Рассмотрим W(p) внешнего контура для управляющего воздействия:
1. Для выходной координаты y2
где q3 – полином знаменателя передаточной функции.
Приравняв знаменатель к 0, получим характеристическое уравнение внешнего контура, найдём корни, пользуясь обратным преобразованием Лапласа, получим переходные функции внешнего контура при управляющем воздействии.
а) 
Расчёт аналитический переходных процессов для y2 при управляющем воздействии.
Определяем передаточные функции для упращенного разомкнутого и замкнутого контуров.
где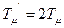 
- малая постоянная времени внутреннего контура.
При упрощении внутренний замкнутый контур представляет апериодическое звено 1-го порядка. Контур внешний представляет собой звено 2-го порядка. Следовательно, порядок системы уменьшается на 1.
Следовательно, передаточные функции разомкнутых и замкнутых систем будут оптимальными. В случае колебательного внутреннего контура система представляет собой оптимальную систему третьего порядка, а при инерционном внутреннем контуре система будет второго порядка, но наименьшая некомпенсируемая постоянная времени при этом будет в два раза больше.
Найдя корни, применив обратное преобразование Лапласа, можно получить выражение для упрощенной переходной функции. Переходная функция будет иметь тот же вид, что и для внутреннего оптимального контура.
б) 
3.3.2 Передаточные функции САР при возмущающем воздействии:
yвх=F(p) yвых=y1
При возмущающем воздействии, когда выходной величиной является выходная величина внутреннего у1 контура, схема САР совпадает со схемой САР при управляющем воздействии, когда выходной величиной является выходная величина внешнего контура, поэтому передаточные функции замкнутой и разомкнутой САР такие же.
1) Передаточная функция разомкнутой и замкнутой САР по возмущающему воздействию для выходной величины внутреннего контора имеет вид
Определим передаточную функцию разомкнутой САР для упрощенного контура
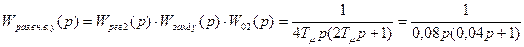
Передаточная функция замкнутой САР
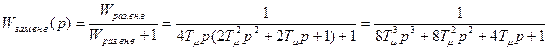
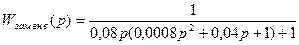
Передаточная функция замкнутой САР для упрощенного контура
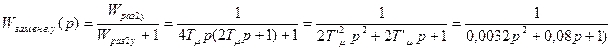
где T’μ=2Tμ=0,04с.
Функции являются оптимальными.
2) Передаточная функция разомкнутой и замкнутой САР по возмущающему воздействию для выходной величины внешнего контора имеет вид
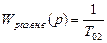
Передаточная функция замкнутой САР
Передаточная функция замкнутой САР для упрощенного контура
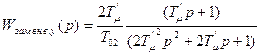
3.4 Аналитический расчет переходных процессов
Используя обратное преобразование Лапласа, находим переходные функции разомкнутых и замкнутых САР при возмущающем и управляющем воздействиям для случаев, когда выходной величиной является выходная величина либо внешнего контура, либо внутреннего контура. По причине сложности и громоздкости расчеты обратного преобразования Лапласа не приводятся.
3.4.1 Расчет переходных процессов по управляющему воздействию
Переходная функция системы при единичном управляющем воздействии, когда выходной величиной является выходная величина внешнего у2 контура
Для упрощенной САР
где T’μ=2Tμ=0,03с.
Переходная функция системы при единичном управляющем воздействии, когда выходной величиной является выходная величина внутреннего у1 контура
Для упрощенной САР
где T’μ=2Tμ=0,04с.
Подставляя значения времени, строим кривые переходных процессов при управляющем воздействии.
Рисунок 3.4. - Кривые переходного процесса при управляющем воздействии
3.4.2 Расчет переходных процессов по возмущающему воздействию.
Рисунок 3.5. – Двухконтурная статическая система САР.
Переходная функция системы при единичном возмущающем воздействии, когда выходной величиной является выходная величина внешнего у2 контура и на выходе системы имеется установившийся процесс с y2=1.
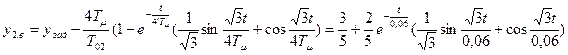
Для упрощенного случая
где T’μ=2Tμ=0,03с.
Переходная функция системы при возмущающем воздействии, когда выходной величиной является выходная величина внутреннего у1 контура, будет оптимальной
Для упрощенной САР
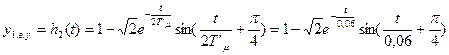
где T’μ=2Tμ=0,03.
Подставляя значения времени, строим кривые переходных процессов при возмущающем воздействии.. Построение начтем с момента времени 23,3Tμ=0,35 c. До этого времени используем построение кривых при управляющем воздействии.
Рисунок 3.6. - Кривые переходного процесса при возмущающем воздействии
3.5 Экспериментальное определение кривых переходных процессов с помощью программы MATLAB
3.5.1 Кривые переходных процессов САР по управляющему воздействию
Используя программу MATLAB и файл SIMULINK, проведем моделирование переходных процессов при управляющем воздействии
Рисунок 3.7 - Кривые переходных процессов САР по управляющему воздействию
3.5.2 Кривые переходных процессов САР по возмущающему воздействию
Для моделирования переходных процессов при возмущающем воздействии необходимо снимать кривые
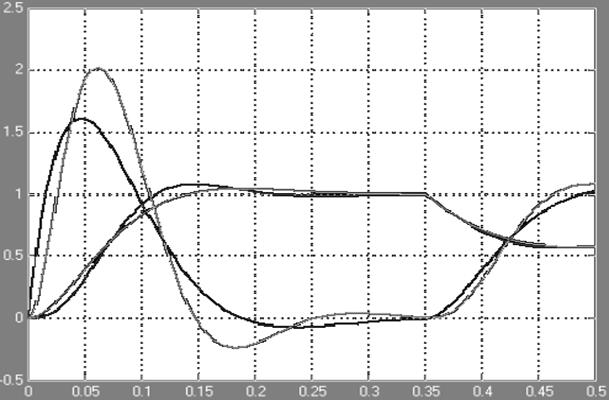
Рисунок 3.8. - Кривые переходных процессов САР по возмущающему воздействию
3.6 Расчет и построение асимптотических ЛАЧХ и ЛФЧХ разомкнутых САР
3.6.1 Управляющее воздействие
Разомкнутая САР при управляющем воздействии, когда выходом является выходная величина внешнего у2 контура, представляет собой последовательно соединенные колебательное и интегрирующее звенья.
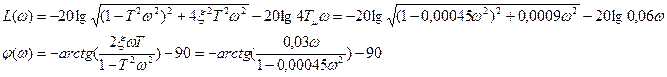
где T =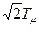 
=0,021 с, а 
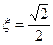=0,707.
Для упрощенного внутреннего контура разомкнутая САР представляет собой последовательно соединенные апериодическое и интегрирующее звено.
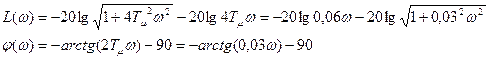
Разомкнутая САР при управляющем воздействии, когда выходом является выходная величина внутреннего у1 контура, представляет собой последовательно соединенные колебательное и пропорциональное звенья.
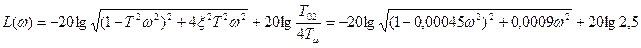
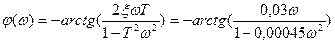
где T = 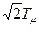=0,021с, а 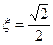=0,707.
Для упрощенного внутреннего контура разомкнутая САР представляет собой последовательно соединенные апериодическое и пропорциональное звено.
где T’μ=2Tμ=0,03с.
3.6.2 Возмущающее воздействие
Разомкнутая САР при возмущающем воздействии, когда выходом является выходная величина внешнего у2 контура, представляет собой интегрирующее звено объекта регулирования.
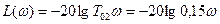
Для упрощенного случая функция останется такой же.
Разомкнутая САР при возмущающем воздействии, когда выходом является выходная величина внутреннего у2 контура, будет аналогична разомкнутой САР, когда воздействие управляющее, а выходная величина – выход внешнего у2 контура регулирования.
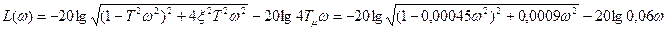
где T = 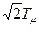=0,021с, а 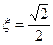=0,707.
То же самое и для упрощенного контура
3.6.3.Построение ЛАЧХ и ЛФЧХ при управляющем воздействии представлены на рис. 3.9. и 4, а при возмущающем на рис. 4.1. и 4.2.
Рисунок-3.9. Логарифмические частотные характеристики разомкнутых САР при управляющем воздействии внешнего контура
Рисунок 4. - Логарифмические частотные характеристики разомкнутых САР при управляющем воздействии внутреннего контура
Рисунок 4.1 - Логарифмические частотные характеристики разомкнутых САР при возмущающем воздействии внешнего контура
Рисунок 4.2 - Логарифмические частотные характеристики разомкнутых САР при возмущающем воздействии внутреннего контура
3.7 Выводы
Т.к. регулятор внутреннего контура содержит интегрирующее звено, то САР является астатической по управляющему воздействию. Регулятором внешнего контура является пропорциональное звено, поэтому САР – статическая по возмущающем воздействию. Статическая ошибка, возникающая при возмущающем воздействии равна 4Tμ/T20=0,667, что подтверждается и аналитическими расчетами и экспериментом. Замена колебательного звена внутреннего контура на апериодическое с удвоенной наименьшей некомпенсируемой постоянной времени приводит к тому, что у системы уменьшается перерегулирование и время регулирования. Сравнительные данные кривых представлены в таблице 9.
Таблица 9 - Показатели качества САР.
| Показатель качества САР | Управляющее воздействие | Возмущающее воздействие | ||||||
| у1 | y2 | y1упр | y2упр | у1 | y2 | y1упр | y2упр | |
| σ, % | - | 8,1 | - | 4,3 | 8,1 | 4,3 | 4,3 | |
| Tрег1/Тμ | ||||||||
| Tрег2/Тμ | ||||||||
| T1/Тμ | ||||||||
| Δ | - | - | - | - | - | 0,66 | - | 0,66 |
| h, дБ | - | ∞ | ∞ | |||||
| g, град |
4. Расчет и исследование двухконтурной астатической САР
4.1 Структурная схема САР, настроенной по симметричному оптимуму
Определение параметров САР
Из способа оптимизации по техническому оптимуму следует, что для получения астатической характеристики в контуре регулирования надо вводить в систему регулятор с интегрирующей составляющей. На нашу систему действует как управляющее, так и возмущающее воздействие. Внутренний контур регулирования содержит в регуляторе интегрирующее звено, и система является астатической по управляющему воздействию. Однако в нашей двухконтурной системе, рассмотренной в п. 3, регулятор – пропорциональное звено, поэтому возмущающее воздействие приводит к появлению статической ошибки.
Часто на практике требуется получение системы астатической и по управлению, и по возмущению, где статическая ошибка отсутствует полностью. Для этого в систему необходимо ввести второе интегрирующее звено – регулятор с интегральной составляющей. При этом система станет как астатической (по управляющему воздействию и по возмущающему воздействию), так и неустойчивой, потому что ЛАЧХ будет пересекать ось абсцисс с наклоном -40 дБ/дек, что является признаком неустойчивости. В этом случае необходимо изменить ЛАЧХ системы таким образом, чтобы частота среза соответствовала участку ЛАЧХ с наклоном -20 дБ/дек. Переход с -40 дБ/дек на -20 дБ/дек должен происходить на октаву раньше, следовательно, получаем характеристику, которая будет симметрична относительно частоты среза. Такая система будет устойчивой. Закон такой оптимизации назван симметричным оптимумом по виду желаемой ЛАЧХ. Система, оптимизированная по такому оптимуму – система с двукратным интегрированием, астатическая по возмущающему и управляющему воздействию. ЛАЧХ такой системы представлена на рисунке 18.
Передаточная функция системы построенной по симметричному оптимуму
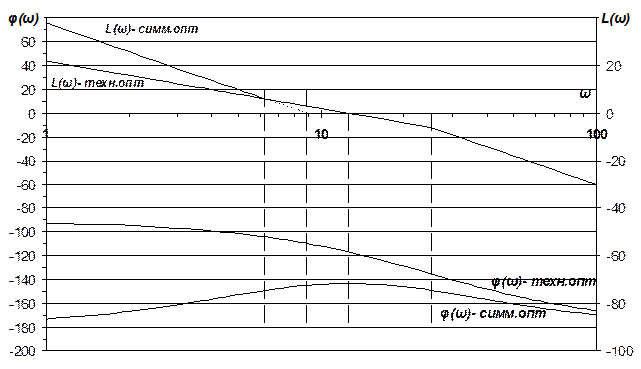
Рисунок 4.3. - ЛАЧХ системы, построенной по симметричному оптимуму.
Показатели такой схемы: 
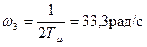
Максимальный запас по фазе наблюдается при частоте среза 
рад/с.
Перерегулирование системы при частоте среза
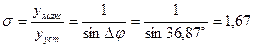
При исследовании системы, оптимизированной по симметричному оптимуму, будем представлять внутренний контур как апериодическое звено первого порядка с постоянной регулирования 
с, т.е. по упрощенной схеме САР.
Чтобы получить систему с передаточной функцией 
, нужно чтобы передаточная функция второго регулятора представляла собой выражение
где 
- передаточная функция регулятора по техническому оптимуму.
Для уменьшения перерегулирования при управляющем воздействии в такой системе перед входом ставят фильтр с передаточной функцией
В соответствии с этими положениями строим структурную схему САР, представленную на рисунке 19.
Рисунок 4.4. - Структурная схема САР, оптимизированной по симметричному оптимуму
Также параллельно будем рассматривать САР с минимальным показателем колебательности у которой передаточной функция регулятора
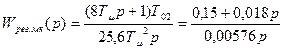
4.2 Расчет и построение ЛАЧХ и ЛФЧХ разомкнутой САР
4.2.1 Система, построенная по симметричному оптимуму, без фильтра
4.2.1.1 Система, построенная по симметричному оптимуму, без фильтра для внешнего контура.
Передаточная функция разомкнутой САР построенной по симметричному оптимуму
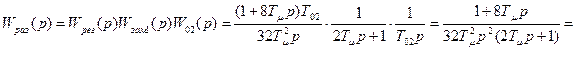
Т.к. разомкнутая САР содержит два интегральных, дифференцирующее и инерционное звено, то
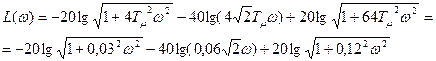
Передаточная функция замкнутого контура
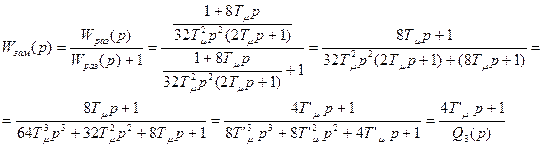
где Т’μ=2Tμ=2·0,015=0,03c – постоянная времени внутреннего контура ;
Q3(р) – знаменатель оптимальной передаточной функции, построенной по техническому оптимуму.
4.2.1.2 Система, построенная по симметричному оптимуму, без фильтра для внутреннего контура.
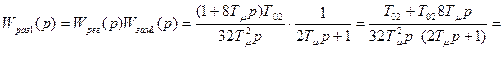
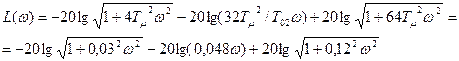
4.2.2 Система, построенная по симметричному оптимуму, с фильтром
4.2.2.1 Система, построенная по симметричному оптимуму, с фильтром для внешнего контура.
Используя выражения, выведенные в пункте 4.2.1, определим передаточную функцию САР с фильтром на управляющем входе
Следовательно, фильтр компенсирует дифференцирующее звено регулятора внешнего контура. Исходя из этого ЛАЧХ и ЛФЧХ
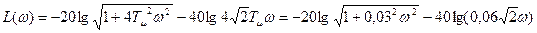
4.2.2.2 Система, построенная по симметричному оптимуму, с фильтром для внутреннего контура.
4.2.3 Система с минимальным показателем колебательности
4.2.3.1 Система с минимальным показателем колебательности для внешнего контура.
Передаточная функция разомкнутой САР построенной по симметричному оптимуму с минимальным показателем колебательности
Т.к. разомкнутая САР содержит два интегральных, дифференцирующее и инерционное звено, то
4.2.3.2 Система с минимальным показателем колебательности для внутреннего контура.
4.2.4 Расчет и построение ЛАЧХ и ЛФЧХ разомкнутых САР
Используя выражения для ЛАЧХ и ЛФЧХ разомкнутых САР, рассчитаем и построим кривые логарифмических частотных характеристик. . Учитывая то, что системы без фильтра и с минимальным показателем колебательности имеют одинаковые ЛФЧХ, обозначим ее как
φ(ω) - м.к.
Рисунок 4.5. - ЛАЧХ и ЛФЧХ разомкнутых систем для внешнего контура.
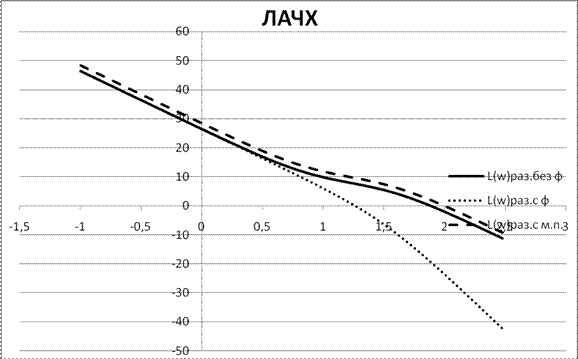
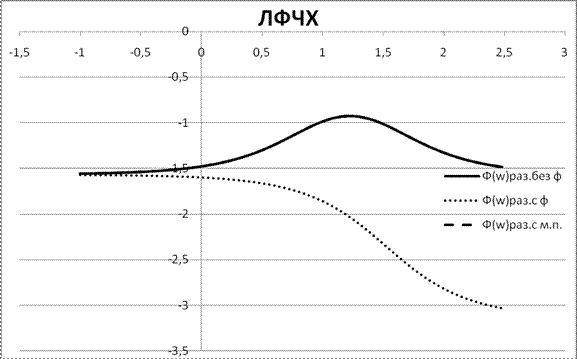
Рисунок 4.6. - ЛАЧХ и ЛФЧХ разомкнутых систем для внутреннего контура.
4.2.5 Связи между прямыми показателями качества и частотными характеристиками
По виду ЛАЧХ и ЛФЧХ можно судить:
1) Система устойчива, если при частоте среза ЛФЧХ меньше 180˚, запас по фазе больше нуля;
2) Время регулирования системы обратно пропорционально частоте среза
;
3) Система устойчива, если запас по амплитуде больше нуля, при частоте достижения ЛФЧХ значения 180˚;
4) Если при частоте среза наклон ЛАЧХ больше -20 дБ/дек, то система устойчивая;
5) Для устойчивости необходим диапазон с наклоном -20 дБ/дек не менее одной декады;
6) По низкочастотной части ЛАЧХ можно судить о статизме системы. Если наклон 0 дБ/дек, то система статическая, если -20 дБ/дек, то система первого порядка статизма, а если -40 дБ/дек – второго порядка статизма.
4.3. Произвести аналитический расчет переходных процессов САР
4.3.1 Расчет переходных процессов
4.3.1.1.Управляющее воздействие
Используя передаточные функции из пункта 4.2, находим переходные функции по управляющему воздействию.
Система, построенная по симметричному оптимуму (без фильтра)
Передаточная функция при управляющем воздействии, когда выходом является выход внешнего у2 контура регулирования: yвх=g(p), yвых=y2
Используя обратное преобразование Лапласа, найдем передаточную функцию по управляющему воздействию для выходной величины внешнего контура
где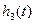 
- переходная функция оптимального процесса, для передаточной функции третьей степени;
- производная этой функции.
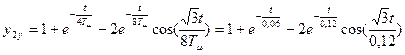
Для выходной величины внутреннего у1 контура
Система, построенная по симметричному оптимуму с фильтром
Передаточная функция при управляющем воздействии, когда выходом является выход внешнего у2 контура регулирования
Переходный процесс будет оптимальным
Передаточная функция по управляющему воздействию для выходной величины внутреннего у1 контура
Для системы с минимальным показателем колебательности стоить кривые переходного процесса не будем по причине сложности вывода переходной функции.
4.3.1.2.Возмущающее воздействие
Передаточная функция по возмущению будет одинаковой как для системы с фильтром, так и для системы без фильтра, т.к. возмущающее воздействие не влияет на фильтр. Это справедливо как для внешнего, так и для внутреннего контуров.
Передаточная функция для выходной величины внешнего контура
В разомкнутой САР будет находиться интегральное звено контура регулирования, а в обратной связи – звено внутреннего контура и регулятор.
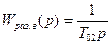
Отсюда передаточная функция замкнутой САР
где Q’3 – знаменатель оптимальной по техническому оптимуму системы третьего порядка, с постоянной времени Т’μ=2Tμ=2·0,015=0,03c.
Переходная функция по возмущающему воздействию для выходной величины внешнего у2 контура (находим с помощью обратного преобразования Лапласа).
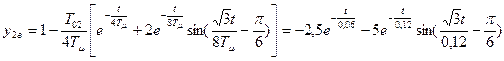
Передаточная функция по возмущающему воздействию для выходной величины внутреннего контура будет равна передаточной функции по управляющему воздействию, когда выходом является выходная величина внешнего контура.
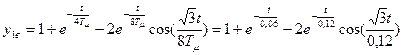
4.3.2 Построение переходных процессов
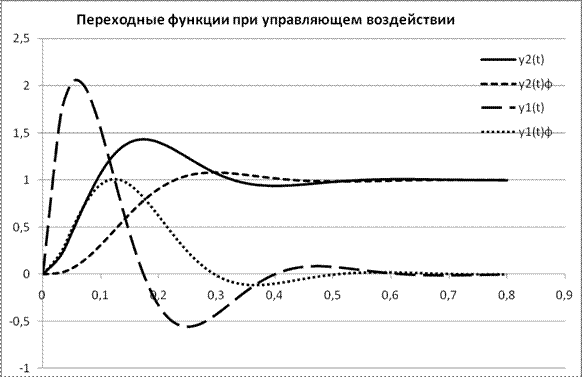
Рисунок 4.7 - Кривые переходного процесса при управляющем воздействии
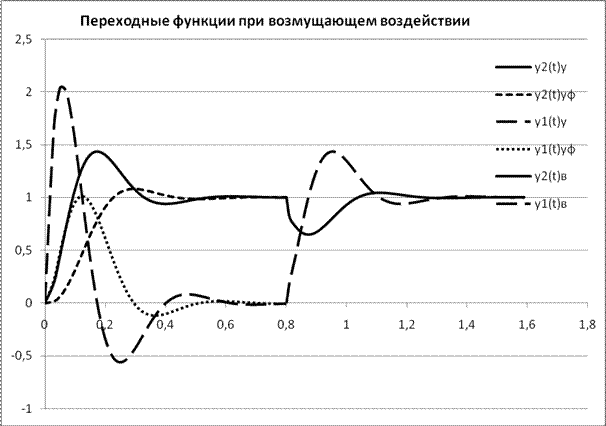
Рисунок 4.8. - Кривые переходного процесса при возмущающем воздействии
4.4 Экспериментальный расчет переходных процессов.
Используя программу MATLAB и файл SIMULINK, произведем расчет переходного процесса для систем построенных по симметричному оптимуму с фильтром и без фильтра. На рисунке 4.9.и 5.1. представлены переходные процессы систем при управляющем воздействии, а на рисунке 5.и 5.2. – при возмущающем воздействии.
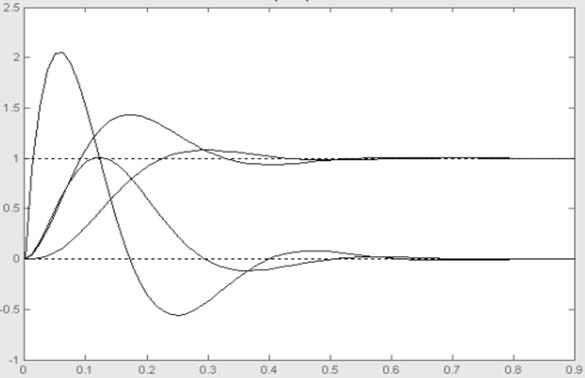
Рисунок 4.9. - Переходные процессы систем при управляющем воздействии
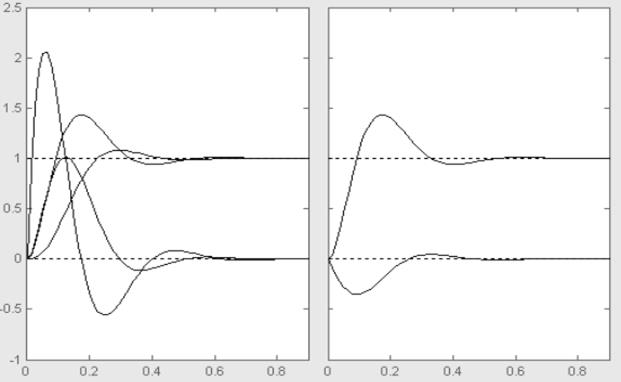
Рисунок 5 - Переходные процессы систем при возмущающем воздействии
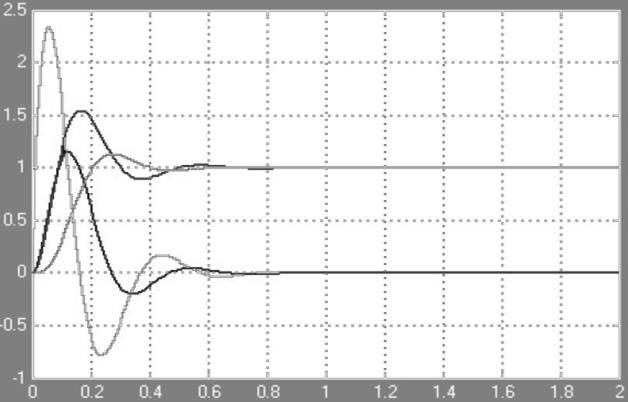
Рисунок 5.1. - Переходные процессы систем при управляющем воздействии
Рисунок 5.2. - Переходные процессы систем при возмущающем воздействии
Таблица - 4.5 Определение показателей САР