Сферические системы координат

Координатные поверхности: сферы с центром в начале (r=const), полуплоскости, ограниченные осью z (φ=const), конусы (с вершиной в начале), для которых ось z является осью (θ=const).

r - длина радиус-вектора, φ - долгота, θ - полярное расстояние

Формулы перехода от сферических координат к декартовым x=r*sin(θ)*cos(φ), y=r*sin(θ)*sin(φ), z=r*cos(φ)

Обобщением всех перечисленных систем координат являются криволинейные системы координат.

Виды графиков.

Классификация графиков по форме графического изображения

Формы графического образа разнообразны: геометрические и фигурные (негеометрические) знаки с плоскостным или объемным изображением. В соответствии с этим различают графики точечные, линейные, плоскостные и пространственные (объемные).

При построении точечных диаграмм в качестве графических образов применяются совокупности точек; при построении линейных - линии, изолинии. Основной принцип построения всех плоскостных диаграмм сводится к тому, что величины изображаются в виде геометрических фигур и, в свою очередь, подразделяются на столбиковые, полосовые, круговые, секторные, квадратные и фигурные.

Классификация графиков по способу построения и задачам изображения

1) Диаграммы являются наиболее распространенным способом графических изображений. Они - графики количественных отношений. Диаграммы применяются для наглядного сопоставления в различных аспектах независимых друг от друга величин.

В зависимости от круга решаемых задач выделяют диаграммы сравнения, структуры, динамики, накопления, рядов распределения величин вариационного ряда.

2) Графические карты - графики количественного распределения признаков по поверхности или во времени. Они подразделяются на универсальные графики и статистические карты (картограммы, картодиаграммы).

3) Контрольные карты - вид графических изображений данных и контрольного диапазона, которые позволяют проводить текущий контроль производственного процесса на промышленном предприятии и прогнозировать его развитие.

4) Взаимосвязанные графики - вид графических изображений, отражающих временное изменение взаимосвязанных разнообразных показателей. Они подразделяются на накопительные и технологические.

Виды номограмм.

Номограммы различают по способу изображения значений переменных (точками или линиями) и по способу задания соответствия между изображениями переменных.

Наиболее распространены следующие номограммы:

1. Транспарантные. В простейшем случае состоит из двух плоскостей: основной плоскости и транспаранта с изображениями на них переменных. Транспарант часто делается из прозрачного материала. Пример транспарантной номограммы — логарифмическая линейка.

2. Сетчатые. Для построения сетчатых номограмм из прямых линий применяются функциональные сетки, простейшими из которых являются логарифмическая и полулогарифмическая. Кроме прямой линии могут применяться и другие, так называемые, разрешающие индексы номограммы: окружности (Годсель), произвольная кривая (Швердт), катеты чертѐжного угольника (Сиглер) и т.д.

3. Из выравненных точек. Для уравнений с тремя переменными применяют три шкалы, которые построены так, что три точки, удовлетворяющие уравнению, лежат на одной прямой — отсюда и название типа номограммы. Именно с них началось развитие номографии — раздела математики, объединяющего теорию и практические методы построения номограмм.

Виды диаграмм.

Наиболее распространенным способом графического изображения статистической информации являются диаграммы. Диаграммы принято подразделять по их форме на следующие виды:

1) Столбиковые диаграммы - изображаются в виде прямоугольников (столбиков), вытянутых по вертикали, высота которых соответствует значению показателя

2) Полосовые диаграммы- Принцип построения тот же, что и столбиковых. Отличие заключается в том, что полосовые (или ленточные) графики представляют значение показателя не по вертикальной, а по горизонтальной оси.

3) Круговые диаграммы - строятся в виде площади кругов, радиусы которых равны корню квадратному из значений показателя.

4) Линейные диаграммы - используются для характеристики вариации, динамики и взаимосвязи. Линейные графики строятся на координатной сетке. Геометрическими знаками служат точки и отрезки прямой, которые их последовательно соединяют в ломаные.

5) Фигурные диаграммы - представляют собой изображение в виде рисунков, силуэтов, фигур, например, головы крупного рогатого скота, какие-либо машины, и др.

Другим признаком подразделения диаграмм является их содержание. По этому признаку они подразделяются на диаграммы сравнения, структурные, динамические, графики связи, графики контроля и др.

9. Классификация планов эксперимента:

- по способу формирования условий (естественных и искусственных);

- по целям исследования (преобразующие, констатирующие, контролирующие, поисковые, решающие);

- по организации проведения (лабораторные, натурные, полевые, производственные и т.п.);

- по структуре изучаемых объектов и явлений (простые, сложные);

- по характеру внешних воздействий на объект исследования (вещественные, энергетические, информационные);

- по характеру взаимодействия средства экспериментального исследования с объектом исследования (обычный и модельный);

- по типу моделей, исследуемых в эксперименте (материальный и мысленный);

- по контролируемым величинам (пассивный и активный);

- по числу варьируемых факторов (однофакторный и многофакторный);

- по характеру изучаемых объектов или явлений (технологические, социометрические) и т.п

Уровень факторов.

Фактором называется измеряемая переменная величина, принимающая в некоторый момент времени определенное значение.

Каждый фактор может принимать в опыте одно из нескольких значений. Такие значения будем называть уровнями. Может оказаться, что фактор способен принимать бесконечно много значений. Однако на практике точность, с которой устанавливается некоторое значение, не беспредельна. Поэтому мы вправе считать, что всякий фактор имеет определенное число дискретных уровней.

Каждый из факторов имеет верхний и нижний уровни, расположенные симметрично относительно некоторого нулевого уровня. Точка в факторном пространстве, соответствующая нулевым уровням всех факторов, называется центром плана. Интервалом варьирования фактора называется некоторое число J, прибавление которого к нулевому уровню дает верхний уровень, а вычитание – нижний.

Фиксированный набор уровней факторов в одном из опытов эксперимента представляет собой лишь одну комбинацию уровней факторов, которая определяет одно из возможных состояний системы. Каждому фиксированному набору уровней факторов соответствует точка в многомерном пространстве, называемом факторным пространством.

Интервалы варьирования.

Интервалом варьирования факторов называется некоторое число (свое для каждого фактора), прибавление которого к основному уровню дает верхний, а вычитание - нижний уровень фактора. Интервал варьирования - это расстояние на координатной оси между основным и верхним или нижним уровнем. Для упрощения записи условий эксперимента и обработки экспериментальных данных масштабы по осям выбираются так, чтобы верхний уровень соответствовал +1, нижний —1, основной 0. Это делается с помощью формулы преобразования

,

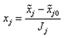где 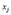– кодированное значение фактора;

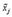– натуральное значение фактора;

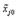– натуральное значение основного уровня;

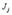– интервал варьирования;

– номер фактора.

Выбор интервалов варьирования является неформализованным этапом планирования эксперимента и производится на основе опыта и интуиции исследователя. При этом следует учитывать точность фиксирования факторов и оценивать силу влияния фактора на величину параметра оптимизации и величину ошибки измерения параметра оптимизации. Это поможет избежать ситуации, при которой интервал варьирования окажется недостаточным для того, чтобы уловить изменение параметра оптимизации.

Важно учитывать характер решаемой задачи. При решении задачи оптимизации для первой серии экспериментов стремятся выбрать такой интервал варьирования, который давал бы возможность для шагового движения к оптимуму. Ориентировочно можно принять, что если интервал составляет не более 10% от области определения, то следует считать его узким, не более 30% - средним, более 30% -широким.