Элементы операционного исчисления

Кафедра высшей математики № 1

Высшая математика

Методические указания и контрольная работа № 3

Минск

БНТУ

Министерство образования Республики Беларусь

БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ

УНИВЕРСИТЕТ

Кафедра высшей математики № 1

Высшая математика

Методические указания и контрольная работа № 3

для студентов-заочников машиностроительных

специальностей

Минск

БНТУ

УДК 512.64 (075.8)

ББК 22.1я7

В 93

С о с т а в и т е л и :

А.Н. Андриянчик, В.А. Казакевич, Н.А. Микулик,
Л.А. Раевская, В.И. Юринок, Т.С. Яцкевич

Р е ц е н з е н т ы :

А.Н. Исаченко, Н.И. Чепелев

Настоящие методические указания и контрольные задания предназначены для студентов-заочников второго курса машиностроительных специальностей БНТУ.

Издание содержит программу по высшей математике, перечень рекомендуемой литературы, основные понятия по теории курса высшей математики, типовые примеры и контрольные задания.

Студент должен изучить теоретический материал по учебнику, разобрать приведенные образцы решения типовых примеров и задач, а затем выполнить контрольные задания по номеру варианта, который совпадает с двумя последними цифрами зачетной книжки (шифра) для первой задачи контрольной работы; номера последующих задач варианта получаются от прибавления к номеру предыдущей задачи числа 20. Например, если шифр содержит две последние цифры 03, номер первой задачи будет 3, номер второй задачи – 23, третьей – 43 и т. д., т. е. номерами этого варианта будут: 3, 23, 43, 63. Если номер шифра больше 20, следует выполнить вариант, номер которого равен двум последним цифрам шифра минус 20. Например, если шифр содержит две последние цифры 31, номерами этого варианта будут: 11, 31, 51, 71.

© БНТУ, 2010

Учебное издание

Высшая математика

Методические указания и контрольная работа № 3

для студентов-заочников машиностроительных

специальностей

составители:

АНДРИЯНЧИК Анатолий Николаевич

КАЗАКЕВИЧ Виктор Александрович

МИКУЛИК Николай Александрович и др.

Ответственный за выпуск О.В. Дубовик

Подписано в печать 14.06.2010.

Формат 60´84¹/₁₆. Бумага офсетная.

Отпечатано на ризографе. Гарнитура Таймс.

Усл. печ. л. 4,53. Уч.-изд. л. 3,54. Тираж 500. Заказ 494.

Издатель и полиграфическое исполнение:

Белорусский национальный технический университет.

ЛИ № 02330/0494349 от 16.03.2009.

проспект Независимости, 65. 220013, Минск.

Содержание

ПРОГРАММА.................................................................. 4

1. РЯДЫ............................................................................ 5

1.1. Числовые ряды. Основные определения.
Признаки сравнения............................................... 5

1.2. Достаточные признаки сходимости рядов
с положительными членами.................................. 8

1.3. Знакопеременные ряды. Абсолютная и условная
сходимость. Знакочередующиеся ряды. Признак
Лейбница............................................................... 11

1.4. Функциональные ряды. Область сходимости
функционального ряда. Степенные ряды.......... 13

1.5. Разложение функции в ряд Тейлора................... 17

1.6. Применение степенных рядов в приближенных
вычислениях.......................................................... 19

1.7. Ряд Фурье функции, заданной на отрезке длиной 2p 24

1.8. Ряд Фурье функции, заданной на отрезке длиной 2l 29

2. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ

НЕСКОЛЬКИХ ПЕРЕМЕННЫХ................................ 31

2.1. Определенный интеграл по фигуре.
Основные понятия и свойства............................ 31

2.2. Вычисление двойных и тройных интегралов
в декартовых координатах................................... 33

2.3. Замена переменных в кратном интеграле.......... 39

2.4. Криволинейные интегралы I и II рода............... 46

2.5. Поверхностные интегралы I и II рода................ 48

2.6. Вычисление криволинейных интегралов I и II рода 49

2.7. Вычисление поверхностных интегралов I и II рода.
Связь между ними................................................ 51

2.8. Формулы Грина, Стокса, Остроградского-Гаусса 54

3. ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ 59

3.1. Оригинал и его изображения.............................. 59

3.2. Основные теоремы операционного исчисления 60

3.3. Отыскание оригинала по изображению............ 62

3.4. Решение дифференциальных уравнений и систем
дифференциальных уравнений операционным методом 65

КОНТРОЛЬНАЯ РАБОТА № 3................................... 68

Рекомендуемая литература........................................... 77

ПРОГРАММА

Ряды

Числовые ряды. Сходимость и сумма ряда. Действия над рядами. Необходимое условие сходимости.

Достаточные признаки сходимости рядов с положительными членами.

Знакопеременные ряды. Абсолютная и условная сходимость. Знакочередующиеся ряды. Теорема Лейбница.

Функциональные ряды. Область сходимости. Равномерная сходимость. Признак Вейерштрасса.

Степенные ряды. Теорема Абеля. Интервал и радиус сходимости степенного ряда.

Ряды Тейлора и Маклорена. Разложение функций в степенные ряды.

Применение рядов к приближенным вычислениям.

Ряды Фурье по тригонометрическим системам. Разложение функций в ряды Фурье. Условия поточечной сходимости и сходимости в среднем. Применение рядов Фурье.

IИнтегральное исчисление функций
нескольких переменных

Определенный интеграл по фигуре, его механический смысл. Свойства интегралов по фигуре.

Вычисление кратных интегралов повторным интегрированием.

Замена переменных в кратных интегралах.

Вычисление криволинейных и поверхностных интегралов I и II рода, их приложения. Формулы Грина, Стокса, Остроградского-Гаусса.

Элементы операционного исчисления

Преобразование Лапласа. Теорема существования и единственности. Класс оригиналов и класс изображений.

Основные теоремы операционного исчисления.

Определение оригинала по изображению с помощью таблиц и второй теоремы разложения.

Решение линейных дифференциальных уравнений и систем операционным методом.

РЯДЫ

1.1. Числовые ряды. Основные определения.
Признаки сравнения

Выражение
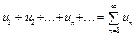, (1)
где ( 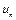) – последовательность чисел, называется числовым рядом, числа 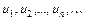– членами ряда, 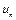– общим членом ряда.

Суммы
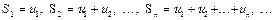(2)
называются частичными суммами ряда (1).

Если существует конечный предел

,

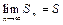то ряд (1) называется сходящимся, а число S - его суммой. Если же 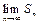не существует или 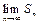=¥, то ряд называется расходящимся.

Если в ряде отбросить первые k членов, то получится ряд
r_k= 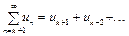, (3)
называемый k-м остатком ряда (1).

Необходимый признак сходимости. Если ряд (1) сходится, то

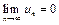. (4)

Следствие. Если 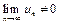, то ряд (1) расходится.

Ряд 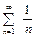называется гармоническим рядом. Для него 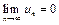, но ряд расходится.

Признаки сравнения. Рассмотрим числовые ряды с неотрицательными членами

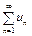; (4)

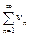. (5)

Теорема 1. Признак сравнения. Если, начиная с некоторого номера, выполняются неравенства 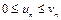, то из сходимости ряда (5) следует сходимость ряда (4), а из расходимости ряда (4) следует расходимость ряда (5).

Теорема 2. Предельный признак сравнения. Если 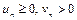для всех 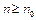и существует конечный предел 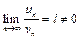, то ряды (4) и (5) сходятся или расходятся одновременно.

Замечание. При использовании признаков сравнения часто применяется ряд 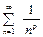, сходящийся при p > 1 и расходящийся при p £ 1 и ряд 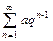, сходящийся при 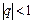и расходящийся при .

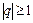Примеры. Исследовать на сходимость ряды и в случае сходимости найти сумму ряда.

1. .
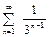Решение. Данный ряд - геометрическая прогрессия со знаменателем 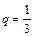. Следовательно, 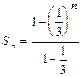, , 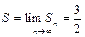ряд сходится.

2. .
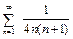Решение. Так как дробь 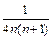представима в виде 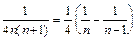, то частичная сумма ряда имеет вид:

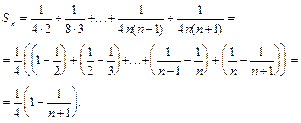
Следовательно, 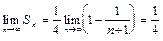, ряд сходится и его сумма равна 1/4.

3.2 + 5 + 8 + 11 + ... .
Решение. Данный ряд - сумма членов арифметической прогрессии с разностью d = 3, поэтому
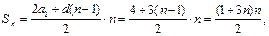
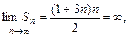ряд расходится.

Проверить, выполняется ли необходимый признак сходимости ряда. В случае выполнения установить, сходится ли ряд с помощью признака сравнения.

4. .
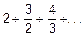Решение. 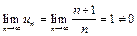, т.е. необходимый признак не выполняется, ряд расходится.

5. .
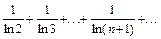Решение. 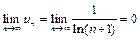, т.е. необходимый признак выполняется. Исследуем сходимость данного ряда с помощью признака сравнения (теорема 1). Рассмотрим расходящийся ряд 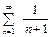. Так как 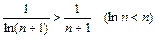, то исходный ряд расходится.

6. .
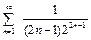Решение. 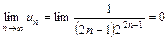. Рассмотрим сходящийся ряд - сумму членов геометрической прогрессии со знаменателем 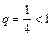. Так как 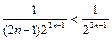, то по теореме 1 исходный ряд сходится.

7. .
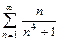Решение. 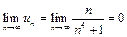. Рассмотрим сходящийся ряд 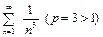и применим предельный признак сравнения (теорема 2): 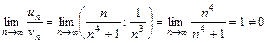. Следовательно, данный ряд сходится.

1.2. Достаточные признаки сходимости рядов
с положительными членами

Для знакоположительных числовых рядов имеют место следующие достаточные признаки, по которым можно установить их сходимость или расходимость.

1. Признак Даламбера. Если для ряда
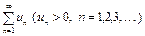(6)
существует 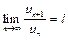, то при l < 1 ряд (6) сходится, при l > 1 - расходится. При l = 1 вопрос о сходимости ряда остается нерешенным.

Пример 1. Исследовать на сходимость ряды с помощью признака Даламбера:
a) ;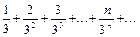

б) .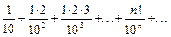

Решение.
a) 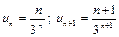. Так как 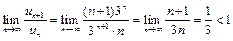, то ряд сходится.
б) 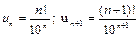; 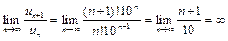. Так как l = ¥, то данный ряд расходится.

2. Радикальный признак Коши. Если для знакоположительного ряда (6) существует предел 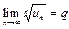, то при q < 1 ряд сходится, при q > 1 - расходится. При q = 1 вопрос о сходимости ряда остается нерешенным.

Пример 2. Исследовать сходимость рядов с помощью радикального признака Коши:
a) ;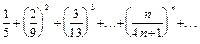
б) .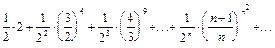

Решение.
а) Так как 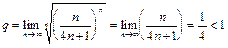, то ряд сходится.
б) в этом случае 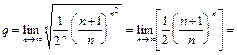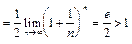. Следовательно, ряд расходится.

3. Интегральный признак Коши. Пусть f(x) - непрерывная, положительная и монотонно убывающая функция, определенная при x ³ 1. Тогда ряд 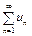и несобственный интеграл 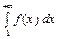сходятся или расходятся одновременно, где f(n)= u_{n .}

Пример 3. Исследовать сходимость рядов с помощью интегрального признака Коши:
a) ;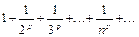
б) .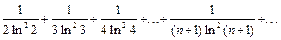

Решение.
a) Исследуемый ряд - 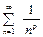. Здесь 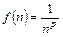. Если p ¹ 1, то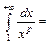

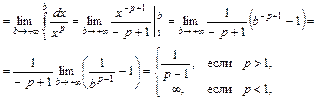
т.е. интеграл сходится при p > 1 и расходится при p < 1. Соответственно и ряд 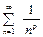сходится, если p > 1 и расходится, если p < 1. При 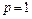имеем 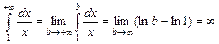, т.е. интеграл расходится. Следовательно, расходится ряд .
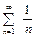б) Исследуемый ряд - 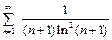. Здесь 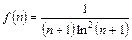. Рассмотрим

Следовательно, данный ряд сходится.

1.3. Знакопеременные ряды. Абсолютная и условная
сходимость. Знакочередующиеся ряды. Признак Лейбница

Ряд 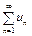(7)
называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.

Теорема 3. Достаточный признак сходимости ряда (7).

Если ряд 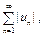(8)
составленный из модулей членов ряда (7), сходится, то ряд (7) также сходится.

Ряд (7) называется абсолютно сходящимся, если сходится ряд (8).

Сходящийся знакопеременный ряд (7) называется условно сходящимся, если ряд (8) расходится.

Ряд вида
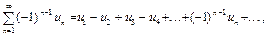(9)
где 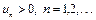, называется знакочередующимся.

Признак Лейбница. Если члены знакочередующегося ряда (9) удовлетворяют условиям:
1) ,
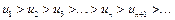2) 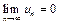,то ряд (9) сходится. Сумма его положительна и не превосходит первого члена 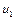.Остаток 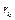такого ряда имеет знак своего первого члена и не превосходит его по модулю: .

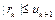Примеры. Исследовать на абсолютную и условную сходимость ряды:

а) ;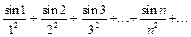

б) ;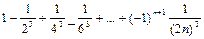

в) .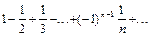

Решения.

а) Ряд из модулей 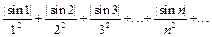сходится по признаку сравнения, так как его члены не превосходят соответствующих членов сходящегося ряда 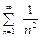. Следовательно, исходный ряд сходится абсолютно.

б) Условия признака Лейбница здесь выполнены: ряд - знакочередующийся, .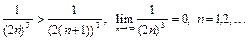

Следовательно, этот ряд сходится. Ряд из модулей 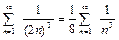также сходится, то есть исходный ряд сходится абсолютно. Найдем сумму данного ряда с точностью 0,01. Для этого возьмем столько его членов, чтобы следующий член ряда был по модулю меньше 0,01. Тогда остаток ряда, начинающийся с этого члена, будет по модулю также меньше 0,01.Модуль четвертого члена 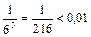, поэтому с точностью 0,01 имеем: .

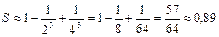в) Данный знакочередующийся ряд сходится по признаку Лейбница, так как 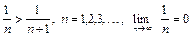.Этот ряд сходится условно, так как ряд 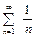,составленный из модулей членов данного ряда, расходится (гармонический ряд).

1.4. Функциональные ряды. Область сходимости
функционального ряда. Степенные ряды

Ряд вида 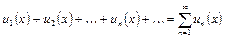, членами которого являются функции 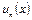, называется функциональным.

Множество всех действительных значений аргумента x, для которых функциональный ряд

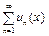(10)

становится сходящимся числовым рядом, называется областью сходимости этого ряда. Функция 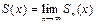, где 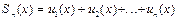, а x принадлежит области
сходимости, называется суммой ряда, функция 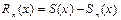– остатком функционального ряда.

Для определения области сходимости ряда (10) можно использовать известные признаки сходимости числовых рядов, считая x фиксированным.

Функциональный ряд (10) называется равномерно сходящимся на промежутке p Ì R, если для любого e > 0 существует номер n_o, не зависящий от x, что для всех n > n_o и для всех x Î p выполняется неравенство 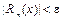, то есть 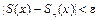, где R_n(x) – остаток ряда.

Признак Вейерштрасса. Если |u_n(x)|£C_n, (n=1,2,...) при 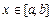и числовой ряд 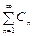сходится, то функциональный ряд (10) сходится на отрезке [a, b] абсолютно и равномерно.

Теорема 4. Если члены сходящегося ряда (10) имеют непрерывные производные при 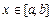и ряд из производных 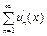сходится равномерно на [a, b], то ряд (10) можно дифференцировать почленно:
.

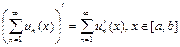Теорема 5. Если члены ряда (10) непрерывны на [a, b] и этот ряд сходится равномерно на отрезке [a, b], то ряд (10) можно
интегрировать почленно:
.

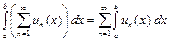Степенным рядом называется функциональный ряд вида

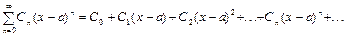, (11)

где C_n и a – действительные числа. Область сходимости степенного ряда (11) имеет один из следующих видов:

(a - R , a + R), [a - R , a + R), ( a - R , a + R], [a - R , a + R].

Число R называется радиусом сходимости, а интервал
(a - R , a + R) – интервалом сходимости степенного ряда (11). Радиус сходимости можно находить по формулам:
,
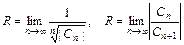если эти пределы существуют. В частных случаях R может быть равен 0 или ¥.

Вопрос о сходимости степенного ряда (11) в концевых точках области сходимости, то есть при x = a - R, x = a + R, исследуется особо (с применением известных признаков сходимости числовых рядов).

Ряды, полученные почленным дифференцированием и интегрированием степенного ряда, имеют тот же радиус и интервал сходимости, и их сумма внутри интервала сходимости равна соответственно производной и интегралу от суммы первоначального ряда.

Пример 1. Найти область сходимости ряда .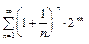

Решение. При фиксированном x этот ряд – знакоположительный. Применим к нему признак Коши. Найдем предел 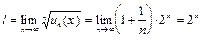; l<1 - при 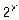< 1, т.е. при x < 0. При l = 1, т.е. при x = 0 данный функциональный ряд станет рядом 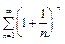. Общий член ряда 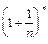при n®¥ стремится к числу e, и поэтому ряд расходится (не выполнен необходимый признак сходимости). Итак, область сходимости данного ряда
(-¥, 0).

Пример 2. Можно ли почленно дифференцировать ряд 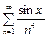в области его сходимости?

Решение. Областью сходимости данного ряда является вся числовая ось R=(-¥, +¥), так как для любого xÎR верно неравенство 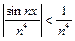, а ряд 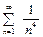сходится. Члены исходного ряда имеют непрерывные производные 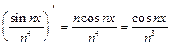, ряд из производных 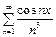сходится равномерно на R по признаку Вейерштрасса. Действительно, верны неравенства 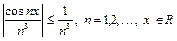, а ряд 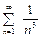сходится. По теореме 4 исходный ряд можно почленно дифференцировать в области R его сходимости, т.е.
.

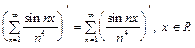Пример 3. Найти область сходимости степенного ряда .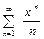

Решение. Находим радиус сходимости ряда. 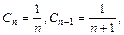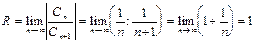. Это означает, что исходный ряд сходится абсолютно при 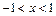. Далее, исследуем сходимость ряда при x = ±1. Если x = 1, то данный ряд становится гармоническим рядом 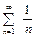, который расходится.
Если x = –1, то получаем знакочередующийся ряд 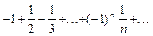, который сходится по признаку Лейбница. Следовательно, областью сходимости ряда является полуинтервал [-1, 1). При 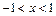ряд сходится абсолютно, при 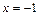– условно.

Пример 4. Найти сумму ряда

.

Решение. Обозначим искомую сумму ряда через S(x), т.е.

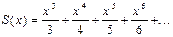. (12)

Можно проверить, что исходный ряд при 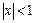сходится абсолютно. Дифференцируем почленно равенство (12):

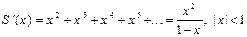
(применена формула суммы членов убывающей геометрической прогрессии). Отсюда, интегрируя и учитывая, что S(0)=0, находим

Пример 5. Найти сумму ряда

.

Решение. Обозначим эту сумму ряда через S(x), т.е. . Данное равенство перепишем так: S(x)=x×Q(x), где 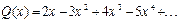. Почленное интегрирование последнего равенства приводит к сумме членов убывающей геометрической прогрессии:

Отсюда найдем Q(x): 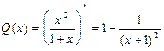, поэтому искомая сумма S(x) такова: .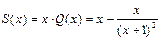