Транспортная задача закрытого типа
Если суммарные мощности поставщиков равны суммарным потребностям потребителей:
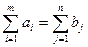 , (5.1)
, (5.1)
то задача называется транспортной задачей закрытого типа.
Построим математическую модель транспортной задачи закрытого типа:
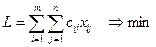 (5.2)
(5.2)
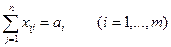 ; (5.3)
; (5.3)
 ; (5.4)
; (5.4)
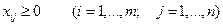 . (5.5)
. (5.5)
Задачу можно сформулировать следующим образом:
построить план  транспортировки груза, удовлетворяющий условиям (5.2); (5.3); (5.4); (5.5).
транспортировки груза, удовлетворяющий условиям (5.2); (5.3); (5.4); (5.5).
Под знаком суммы (5.2) произведение 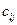
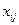 - это затраты на перевозку груза от поставщика
- это затраты на перевозку груза от поставщика 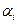 потребителю
потребителю 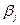 . Условие (5.2) означает, что суммарные транспортные затраты должны быть минимальны. Уравнения (5.3) устанавливают баланс между суммой всех грузов, вывозимых от каждого поставщика и имеющимися у него запасами. Уравнения (5.4) устанавливают баланс между суммой всех грузов, доставляемых каждому потребителю и потребностями этого потребителя. Неравенства (5.5) отражают тот факт, что количество перевозимого груза не может быть отрицательным.
. Условие (5.2) означает, что суммарные транспортные затраты должны быть минимальны. Уравнения (5.3) устанавливают баланс между суммой всех грузов, вывозимых от каждого поставщика и имеющимися у него запасами. Уравнения (5.4) устанавливают баланс между суммой всех грузов, доставляемых каждому потребителю и потребностями этого потребителя. Неравенства (5.5) отражают тот факт, что количество перевозимого груза не может быть отрицательным.
Математическая модель транспортной задачи является математической моделью задачи линейного программирования. Среди множества решений системы ограничений необходимо найти такое неотрицательное решение, при котором целевая функция  принимала бы минимальное значение. Транспортная задача относится к классу широко распространенных на практике задач ЛП. Однако, специфическая форма системы ограничений данной задачи позволяет существенно упростить обычный симплексный метод. Модификация симплексного метода применительно к транспортной задаче называется распределительным методом.
принимала бы минимальное значение. Транспортная задача относится к классу широко распространенных на практике задач ЛП. Однако, специфическая форма системы ограничений данной задачи позволяет существенно упростить обычный симплексный метод. Модификация симплексного метода применительно к транспортной задаче называется распределительным методом.
Решение распределительным методом осуществляется по шагам, и каждому шагу соответствует разбиение переменных на базисные и свободные. Число базисных переменных на каждом шаге равно рангу системы уравнений (5.3), (5.4). Доказано, что ранг системы уравнений (5.3), (5.4) равен 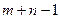 . Поэтому, в закрытой транспортной задаче базисных переменных
. Поэтому, в закрытой транспортной задаче базисных переменных 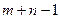 . Так как, общее количество переменных в закрытой транспортной задаче равно
. Так как, общее количество переменных в закрытой транспортной задаче равно 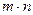 ,то свободных переменных будет ровно
,то свободных переменных будет ровно 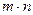 -(
-( 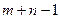 ).
).
При решении транспортной задачи распределительным методом, переходят от одного базисного распределения поставок к другому в сторону не возрастания целевой функции  вплоть до оптимального решения. Для начала такого движения требуется исходное базисное распределение поставок – «опорный план».
вплоть до оптимального решения. Для начала такого движения требуется исходное базисное распределение поставок – «опорный план».
Нахождение первоначального базисного распределения поставок
Задача №5.1.
Рассмотрим пример транспортной задачи, условие которой задано в распределительной таблице.
| поставщики | потребители | запасы | |||
 |  |  | 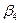 | ||
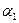 | |||||
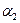 | |||||
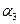 | |||||
| потребности |
Данная задача является задачей закрытого типа.
Те клетки, где будут записываться соответствующие значения базисных переменных (объемы поставок), назовем занятыми. Клетки, соответствующие свободным переменным равным в базисном решении нулю, назовем свободными.
Одним из возможных методов нахождения первоначального базисного распределения поставок является метод «северо-западного угла».
