Характеристика симплекс-метода
В основу решения задачи раскроя в данной курсовой работе положен симплекс-метод, разработанный в конце 40-х годов американским математиком Данцигом. Этот метод используется для решения большого комплекса задач внутризаводского планирования.
Общий вид задачи, решаемой симплекс-методом, следующий:
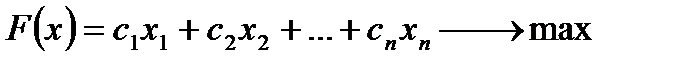
при ограничениях, которые могут быть представлены в виде равенств:


………………………...
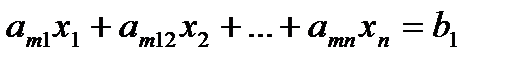
и неравенств:
 .
.
Основная идея симплекс-метода состоит в следующем:
1 принимается за базу одна из возможных программ – отправная (опорный план);
2 осуществляется её пошаговое улучшение, пока не будет получен оптимум по заданной критериальной функции.
Таким образом, проблема сводится к определению отправного варианта программы и нахождению способа улучшения последнего. При этом при формировании первоначального варианта программы создаётся как бы запас, возможность реализации в виде резервов тех ресурсов, которые регламентируются в сложившейся производственной ситуации. В процессе преобразований одни переменные вводятся в план, другие исключаются из него. С каждым шагом план приближается к оптимальному и в конечном итоге приходит к нему, если в условиях задачи нет противоречия. За счёт пошагового перераспределения ресурсов между планируемыми на выпуск изделиями находится такое сочетание номенклатуры и количества этих изделий, которое является наилучшим с точки зрения достижения оптимальности и использования имеющихся ресурсов.
Решение задач симплекс-методом предусматривает выполнение следующих процедур:
1 Формирование целевой функции;
2 Определение ограничительных условий – функциональных ограничений, которые могут иметь вид неравенств,
3 Преобразование ограничений из неравенств в систему равенств путём ввода вспомогательных, свободных переменных;
4 Построение исходной симплексной таблицы-матрицы, в которой в формируемый план входят только свободные переменные;
5 Ввод в исходный вариант плана реальных переменных и прежде всего тех, которые в наибольшей степени реализуют целевую функцию;
6 Определение числового значения вводимой переменной – величины программы.
При этом каждый из показателей, характеризующих ограничительное условие, делится на соответствующий коэффициент при вводимом переменном – удельный расход данного ресурса. Тогда наименьшее частное определит максимально возможное в условиях принятых ограничений использование ресурсов при заданном критерии оптимальности. Полученный результат вводится в соответствующую строку формируемого плана симплексной таблицы. По этой строке матрицы весь ресурс исчерпан, она является «узким местом» и подлежит выводу. На её место вводится другая строка, предварительно пересчитанная. Формируется новый вариант симплексной таблицы, соответствующий к-той итерации.
Пересчёт строки ведётся по генеральному или базовому элементу, находящемуся на пересечении вводимой и выводимой переменных. Каждый элемент вводимой строки необходимо разделить на генеральный элемент. Все остальные элементы матрицы пересчитываются по столбцам по следующим правилам:
1 Значения столбцов, в которых в строке генерального элемента стоит ноль, переносятся без изменения;
2 При пересчёте остальных столбцов необходимо из первоначального значения соответствующих элементов вычесть произведение элемента вводимой строки этого столбца на соответствующий коэффициент в столбце генерального элемента.
Непосредственно в курсовой работе применяется двойственный симплекс-метод, придуманный в 1954 г. Этот метод даёт преимущество в тех случаях, когда ограничения имеют вид – меньше или равно. В этом случае не требуются искусственные переменные, уменьшается размер симплексной таблицы, упрощается и ускоряется решение. Суть метода такова: вводят дополнительные переменные для придания системе канонического вида, затем для получения недопустимого базисного решения все элементы ограничений умножаются на -1. Строится симплексная таблица (обычным образом). Находится допустимое и оптимальное решение.
При построении второй и последующей симплексных таблиц при поиске ключевой строки находится минимум отношения элементов b – столбца к элементам ключевого столбца, если эти элементы одного знака. Для поиска ключевого столбца находится минимальное отношение элемента z – строки к отрицательным элементам ключевой строки.
Обозначаем через xij количество единиц j-го материала, раскраиваемых по i-му способу (всего таких переменных будет p * s). Переменные xij , очевидно, должны удовлетворять ограничениям:
Xij ≥0 (i=1, 2, … , p и j=1, 2, … , s),


Где x – число комплектов изготавливаемых изделий.
Задача заключается в максимизации z = x при условиях первых двух формул.
Дальнейшее решение задачи проводится симплексным методом. В частном случае, когда на обработку поступает материал только одного образца (т.е. s=1), в количестве a единиц, модель принимает более простой вид: максимизировать z=j при условиях:
xi≥0 (i=1, 2, … , p),


