Как определяются опорные реакции?
Способы определения опорных реакций изучаются в курсе теоретической механики. Поэтому мы остановимся только на некоторых практических вопросах, касающихся методики их вычисления, в частности для шарнирно опертой балки с консолью (рис. 7.4).
Для такой балки нам необходимо найти три упомянутые ранее реакции: 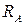 ,
,  и
и  . Направления этих реакций мы выбираем произвольно. Направим, например, обе вертикальные реакции вверх, а горизонтальную реакцию – влево. Для вычисления их значений можно составить три уравнения статики:
. Направления этих реакций мы выбираем произвольно. Направим, например, обе вертикальные реакции вверх, а горизонтальную реакцию – влево. Для вычисления их значений можно составить три уравнения статики:
1) Сумма проекций всех сил (активных и реактивных) на ось z равна нулю:
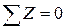 .
.
Поскольку в сопротивлении материалов принято считать, что на балку действуют только вертикальные нагрузки (перпендикулярные к ее оси), то из этого уравнения мы легко находим, что горизонтальная реакция неподвижной шарнирной опоры 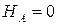 .
.
2) 
Сумма моментов всех сил относительно опоры А равна нулю:
 .
.
Договоримся о правиле знаков для момента силы.
Будем считать момент силы положительным, если он вращает балку относительно некоторой точки против хода часовой стрелки.
Подчеркнем, что в этом правиле говорится о моменте, который вращает балку. Это очень важное замечание, и оно станет ясным из дальнейшего изложения (см. вопрос 7.16). Поэтому слово «вращает» и выделено в правиле жирным шрифтом.
Кстати, происхождение термина «момент силы» неизвестно. По-видимому, этот термин произошел от латинского слова movimentum, что означает способность силы двигать (вращать) объект, используя какой-либо рычаг (плечо силы).
Вернемся к рассматриваемому примеру. Предварительно нам необходимо найти равнодействующую распределенной погонной нагрузки. Очевидно, что она равна площади эпюры этой нагрузки 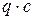 и приложена в центре тяжести этой эпюры, то есть посредине участка длиной
и приложена в центре тяжести этой эпюры, то есть посредине участка длиной  .
.
Тогда

 кН.
кН.
3) Сумма моментов всех сил относительно опоры B равна нулю:

или
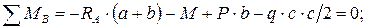
 кН.
кН.
Знак «минус» в полученном результате говорит о том, что предварительное направление опорной реакции 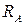 нами было выбрано неверно. Заменим направление реакции
нами было выбрано неверно. Заменим направление реакции 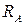 на противоположное (см. рис. 7.4) и про знак «минус» навсегда забудем.
на противоположное (см. рис. 7.4) и про знак «минус» навсегда забудем.
Теперь сделаем проверку.
Сумма проекций всех сил на ось y должна быть равна нулю:
 .
.
Силы, направление которых совпадает с положительным направлением оси y, проектируются (или проецируются) на эту ось со знаком «плюс»:

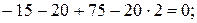
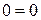 ,
,
то есть опорные реакции найдены нами верно.
Теперь перейдем к жестко защемленной балке. В этом случае для определения опорных реакций составляются следующие уравнения статики:
 .
.
Из первого уравнения определяется реакция  (обычно она равна нулю), из второго –
(обычно она равна нулю), из второго –  , а из третьего – момент в заделке
, а из третьего – момент в заделке  . Проверка, как правило, не производится.
. Проверка, как правило, не производится.
7.15. Какие балки называются статически неопределимыми?
Балки, для которых не удается определить все опорные реакции из уравнений статики, называются статически неопределимыми.
Мы еще вернемся к этому вопросу и остановимся на нем подробнее.
7.16. С какой целью строятся эпюры перерезывающих сил  и изгибающих моментов
и изгибающих моментов 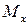 ?
?
Они строятся для наглядного представления о характере изменения этих внутренних силовых факторов по длине балки, а также с целью определения тех опасных сечений, в которых возникают, соответственно, наибольшие касательные и нормальные напряжения.
Еще раз напомним, что:
1) перерезывающая сила численно равна алгебраической сумме всех внешних сил (активных и реактивных), действующих на рассматриваемую нами часть балки;
2) изгибающий момент численно равен алгебраической сумме моментов этих же сил относительно главной центральной оси, проходящей через центр тяжести рассматриваемого поперечного сечения (иногда говорят просто – относительно самого сечения).
7.17. Какие правила знаков используются для вычисления перерезывающей силы  и изгибающего момента
и изгибающего момента 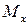 ?
?
Эти правила, к сожалению, непростые для запоминания, формулируются следующим образом.
 Для перерезывающей силы: внешняя сила, действующая на рассматриваемую часть балки и стремящаяся «повернуть» эту часть относительно сечения по ходу часовой стрелки, вызывает в сечении положительную перерезывающую силу. Такая внешняя сила входит в алгебраическую сумму для определения
Для перерезывающей силы: внешняя сила, действующая на рассматриваемую часть балки и стремящаяся «повернуть» эту часть относительно сечения по ходу часовой стрелки, вызывает в сечении положительную перерезывающую силу. Такая внешняя сила входит в алгебраическую сумму для определения  со знаком «плюс» (рис. 7.5, а).
со знаком «плюс» (рис. 7.5, а).
Заметим, что и положительная перерезывающаясила  , в свою очередь, тоже«стремится вращать»любую из частей балки по ходу часовой стрелки.
, в свою очередь, тоже«стремится вращать»любую из частей балки по ходу часовой стрелки.
Теперь приведем правило знаков для изгибающего момента: внешняя нагрузка, изгибающая рассматриваемую часть балки выпуклостью вниз, вызывает в сечении положительный изгибающий момент. Поэтому момент, создаваемый такой нагрузкой, входит в алгебраическую сумму для определения 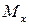 со знаком «плюс» (рис. 7.5, б).
со знаком «плюс» (рис. 7.5, б).
Обращаем внимание уважаемого Читателя на то, что в этом правиле говорится об изгибающем моменте, то есть моменте, который изгибает балку, а не вращает ее.
Из рис. 7.5, б видно, что положительный изгибающий момент 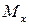 как бы «стремится изогнуть» любую из частей балки также выпуклостью вниз.
как бы «стремится изогнуть» любую из частей балки также выпуклостью вниз.
Для удобства определения знака изгибающего момента рекомендуется поперечное сечение балки мысленно представлять в виде условной жесткой заделки.
7.18. Какие дифференциальные зависимости существуют между интенсивностью равномерно распределенной нагрузки  , перерезывающей силой
, перерезывающей силой  и изгибающим моментом
и изгибающим моментом 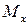 ?
?
Эти зависимости, имеющие вид:
 , (7.1)
, (7.1)
впервые были установлены в 1852 г. немецким ученым Иоганом Вильгельмом Шведлером (Schwedler,1823 – 1894 гг.). Позднее они были получены и русским ученым Дмитрием Ивановичем Журавским (1821 – 1891 гг.). Формулы (7.1) используются для контроля правильности построения эпюр  и
и 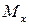 . Очень часто их называют также формулами Шведлера – Журавского.
. Очень часто их называют также формулами Шведлера – Журавского.
Необходимо подчеркнуть, что в приведенных формулах распределенная нагрузка q считается положительной, если она направлена вниз.
7.19. Какие правила используются при построении и проверке эпюр  и
и 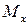 ?
?
Приведем основные правила, которые вытекают непосредственно из метода сечений, а также являются следствием формул (7.1) Шведлера – Журавского. Отметим, что некоторые из этих правил справедливы только при обходе эпюр и
и 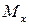 слева направо:
слева направо:
1) Если на некотором участке балки отсутствует распределенная нагрузка (  ), то эпюра
), то эпюра  на этом участкепредставляет собой прямую, параллельную оси балки (рис. 7.6). Действительно, поскольку
на этом участкепредставляет собой прямую, параллельную оси балки (рис. 7.6). Действительно, поскольку  , то и
, то и  . Следовательно,
. Следовательно, 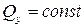 .
.
Эпюра моментов на этом же участке (где  ) – также прямая линия. Причем, если
) – также прямая линия. Причем, если  , то прямая линия идет вверх, а если
, то прямая линия идет вверх, а если  , прямая линия идет вниз. Если
, прямая линия идет вниз. Если  , то изгибающий момент постоянен, поскольку
, то изгибающий момент постоянен, поскольку 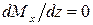 .
.
2) Под сосредоточенной силой P на эпюре  (рис. 7.6, а) имеется скачок на величину этой силы и по ее направлению, а на эпюре
(рис. 7.6, а) имеется скачок на величину этой силы и по ее направлению, а на эпюре 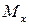 –излом, угол которого всегда направлен навстречу нагрузке.
–излом, угол которого всегда направлен навстречу нагрузке.
3) Если на некотором участке балки имеется равномерно распределенная нагрузка, то эпюра  на этом участкепредставляет собой наклонную прямую (рис. 7.6, б), идущую вниз, если нагрузка
на этом участкепредставляет собой наклонную прямую (рис. 7.6, б), идущую вниз, если нагрузка  направлена вниз, и идущую вверх, если нагрузка
направлена вниз, и идущую вверх, если нагрузка  направлена вверх. Эпюра
направлена вверх. Эпюра 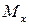 на этом участке, согласно третьей формуле (7.1), изменяется по квадратичной параболе, причем выпуклость параболы всегда направлена навстречу нагрузке.
на этом участке, согласно третьей формуле (7.1), изменяется по квадратичной параболе, причем выпуклость параболы всегда направлена навстречу нагрузке.
Если эпюра перерезывающей силы проходит через нулевое значение, то в этом сечении балки на эпюре 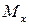 имеется экстремум (последнее вытекает из зависимости
имеется экстремум (последнее вытекает из зависимости 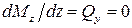 ). Отметим, что в точках, соответствующих началу и концу участка, в пределах которого действует распределенная нагрузка, параболическая и прямолинейная части эпюры
). Отметим, что в точках, соответствующих началу и концу участка, в пределах которого действует распределенная нагрузка, параболическая и прямолинейная части эпюры 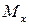 переходят одна в другую плавно (без излома).
переходят одна в другую плавно (без излома).

4) Сосредоточенный внешний момент M (рис. 7.6, в) никак не отражается на эпюре  . На эпюре
. На эпюре 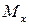 в месте приложенияэтого моментаимеется скачок на его величину.
в месте приложенияэтого моментаимеется скачок на его величину.
Заметим, что построение эпюр перерезывающих сил и изгибающих моментов ввел в практику расчета стержней на изгиб в 1859 г. французский ученый Жак Антуан Шарль Бресс (Bresse, 1822 – 1883 гг.).
7.20. Можно ли продемонстрировать порядок построения эпюр  и
и 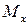 на конкретном числовом примере?
на конкретном числовом примере?
Да, конечно. Покажем порядок построения этих эпюр на рассмотренном выше примере балки (см. рис. 7.4).
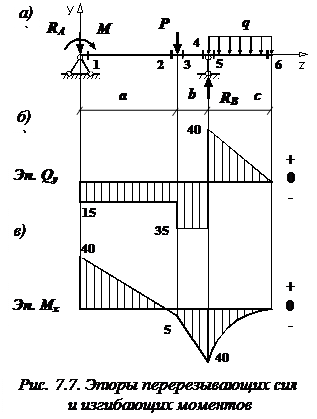 Сначала разобьем всю длину балки на отдельные участки
Сначала разобьем всю длину балки на отдельные участки
(рис. 7.7, а). Границами этих участков являются точки приложения сосредоточенных усилий (активных или реактивных), а также точки, соответствующие началу и окончанию действия распределенной нагрузки. Таких участков получается три.
Затем по границам этих участков наметим шесть поперечных сечений, в которых мы и будем вычислять значения перерезывающих сил и изгибающих моментов.
Сечение 1. Отбросим мысленно правую часть балки (закроем ее листком бумаги, совмещая левый край листка с рассматриваемым сечением). Перерезывающая сила, возникающая в этом сечении, должна уравновесить все внешние силы, которые мы видим. В данном случае мы видим только реакцию опоры, направленную вниз. Таким
образом,
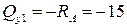 кН.
кН.
Знак «минус» нами взят потому, что сила 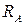 вращает видимую нами часть балки относительно сечения (края листка бумаги) против хода часовой стрелки.
вращает видимую нами часть балки относительно сечения (края листка бумаги) против хода часовой стрелки.
Изгибающий момент в сечении равен алгебраической сумме моментов всех усилий, которыемы видим, относительно рассматриваемого сечения (то есть относительно края листка бумаги).
Мы видим два усилия: реакцию опоры 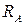 и момент M. Однако у силы
и момент M. Однако у силы 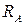 плечо практически равно нулю. Поэтому
плечо практически равно нулю. Поэтому
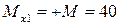 кН·м.
кН·м.
Здесь знак «плюс» нами взят потому, что внешний момент M изгибает видимую нами часть балки выпуклостью вниз.
Заметим, что при определении знака изгибающего момента мы мысленно освобождаем видимую нами часть балки от всех фактических опорных закреплений и представляем ее как бы защемленной в рассматриваемом сечении (то есть левый край листка бумаги нами мысленно представляется жесткой заделкой).
Сечение 2. По-прежнему будем закрывать листком бумаги всю правую часть балки. Теперь, в отличие от первого сечения, у силы 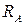 появилось плечо, равное а. Поэтому
появилось плечо, равное а. Поэтому
 кН;
кН;
 кН·м.
кН·м.
Сечение 3. Сначала закроем правую часть. Получим:
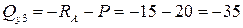 кН;
кН;
 кН ·м.
кН ·м.
Теперь, для контроля правильности вычислений, закроем листком бумаги левую часть балки. Мы видим реакцию правой опоры 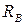 и распределенную нагрузку q. Равнодействующая погонной нагрузки равна
и распределенную нагрузку q. Равнодействующая погонной нагрузки равна 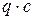 . Она приложена посредине участка длиной
. Она приложена посредине участка длиной  . Поэтому
. Поэтому
 кН;
кН;
 кН ·м.
кН ·м.
То есть все верно.
Сечение 4. Закрываем листком бумаги левую часть балки. Тогда
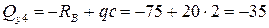 кН;
кН;
 кН ·м.
кН ·м.
Сечение 5. По-прежнему закроем левую часть балки. Будем иметь:
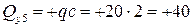 кН;
кН;
 кН ·м.
кН ·м.
Сечение 6. Опять закроем левую часть балки. Получим:
 .
.
По найденным значениям строим эпюры перерезывающих сил  (рис. 7.7, б) и изгибающих моментов
(рис. 7.7, б) и изгибающих моментов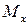 (рис. 7.7, в).
(рис. 7.7, в).
Убеждаемся в том, что под незагруженными участками балки эпюра перерезывающих сил идет параллельно ее оси. Под распределенной нагрузкой q – по прямой, имеющей наклон вниз. На эпюре  имеется три скачка: под реакцией
имеется три скачка: под реакцией 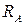 – вниз на 15 кН, под силой P – вниз на 20 кН и под реакцией
– вниз на 15 кН, под силой P – вниз на 20 кН и под реакцией 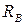 – вверх на 75 кН.
– вверх на 75 кН.
На эпюре изгибающих моментов мы видим изломы под сосредоточенной силой P и под опорными реакциями. Углы изломов направлены навстречу этим силам. Под распределенной нагрузкой q эпюра изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке. В сечении 6 на эпюре 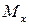 – экстремум, поскольку эпюра перерезывающей силы в этом месте проходит здесь через нулевое значение.
– экстремум, поскольку эпюра перерезывающей силы в этом месте проходит здесь через нулевое значение.
В заключение отметим, что, как это ни странно, студенты зачастую неверно «штрихуют» эпюры. Смысл «штриховки» заключается в том, что каждая ее линия (ордината эпюры) в принятом масштабе дает значение внутреннего усилия, возникающего в соответствующем поперечном сечении стержня. Поэтому так любимая студентами «штриховка» эпюр под углом  лишена всякого смысла.
лишена всякого смысла.
7.21. Как формулируется гипотеза плоских сечений при изгибе балки?
Мысленно нанесем на боковой поверхности недеформированной балки сетку, состоящую из продольных и поперечных (перпендикулярных к оси балки) прямых линий. В результате изгиба балки мы увидим, что продольные линии примут криволинейное очертание, а поперечные линии практически останутся прямыми и перпендикулярными к изогнутой оси балки. Таким образом, поперечные сечения, плоские и перпендикулярные к оси балки до деформации, остаются плоскими и перпендикулярными к изогнутой оси после ее деформации.
Это обстоятельство свидетельствует о том, что при изгибе (как при растяжении и кручении) выполняется гипотеза плоских сечений.
7.22. Какие еще допущения принимаются при выводе формулы для нормальных напряжений при чистом изгибе балки и чему они равны?
Помимо упомянутой гипотезы плоских сечений принимается ещё одно допущение: считается, что продольные волокна балки при ее изгибе не надавливают друг на друга (то есть напряжения 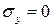 ).
).
Эти два допущения вместе называют гипотезой Бернулли.
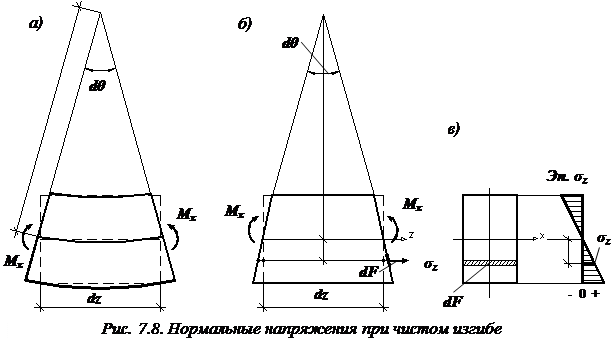
Рассмотрим балку прямоугольного поперечного сечения, испытывающую чистый изгиб (  ). Двумя бесконечно близкими поперечными сечениями выделим элемент балки длиной
). Двумя бесконечно близкими поперечными сечениями выделим элемент балки длиной 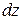 (рис. 7.8. а). В результате изгиба поперечные сечения балки повернутся, образовав между собой угол
(рис. 7.8. а). В результате изгиба поперечные сечения балки повернутся, образовав между собой угол 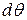 . Пусть при этом верхние волокна испытывают сжатие, а нижние – растяжение. Радиус кривизны нейтрального волокна обозначим
. Пусть при этом верхние волокна испытывают сжатие, а нижние – растяжение. Радиус кривизны нейтрального волокна обозначим 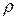 .
.
Для удобства далее будем условно считать, что волокна изменяют свою длину, оставаясь при этом прямыми (рис. 7.8. б).
Тогда абсолютное и относительное удлинения волокна, отстоящего на расстоянии y от нейтрального волокна, будут соответственно равны:
 .
.
По закону Гука
 . (7.2)
. (7.2)


Покажем теперь, что продольные волокна, не испытывающие при изгибе балки ни растяжения, ни сжатия, проходят через главную центральную ось x.
Поскольку длина балки (а точнее, длина ее оси) при изгибе не изменяется, продольное усилие N, возникающее в поперечном сечении, должно равняться нулю. Элементарное продольное усилие 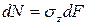 . Тогда
. Тогда
 ,
,
или, с учетом выражения (7.2),
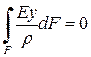 .
.
Множитель 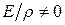 можно вынести за знак интеграла, так как он не зависит от переменной интегрирования. В итоге получим
можно вынести за знак интеграла, так как он не зависит от переменной интегрирования. В итоге получим
 . (7.3)
. (7.3)
Выражение (7.3) представляет собой статический момент площади поперечного сечения балки относительно нейтральной оси x. Он равен нулю только в том случае, когда эта ось проходит через центр тяжести поперечного сечения.
Следовательно, нейтральная ось (или нулевая линия) при изгибе балки проходит через центр тяжести поперечного сечения.
Установленный факт, кстати, подчеркивает важность темы, рассмотренной нами выше в беседе 4.
Очевидно, что изгибающий момент связан с нормальными напряжениями, возникающими в точках поперечного сечения стержня. Поэтому перейдем к его вычислению. Элементарный изгибающий момент, создаваемый элементарной силой  , равен
, равен 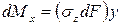 , тогда
, тогда
 , (7.4)
, (7.4)
где  – момент инерции поперечного сечения относительно нейтральной оси x, а отношение
– момент инерции поперечного сечения относительно нейтральной оси x, а отношение  называется кривизной оси балки.
называется кривизной оси балки.
Произведение 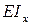 в формуле (7.4) называется жесткостью поперечного сечения балки при изгибе. Чем больше эта величина, тем меньше кривизна оси балки
в формуле (7.4) называется жесткостью поперечного сечения балки при изгибе. Чем больше эта величина, тем меньше кривизна оси балки 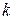 при том же значении изгибающего момента.
при том же значении изгибающего момента.
Формула (7.4) представляет собой закон Гука для стержня при изгибе: изгибающий момент, возникающий в поперечном сечении, пропорционален кривизне оси балки.
Выражая из (7.4) радиус кривизны 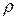 и подставляя его значение в (7.2), получим окончательно следующую формулу для нормальных напряжений
и подставляя его значение в (7.2), получим окончательно следующую формулу для нормальных напряжений 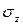 , возникающих в произвольной точке поперечного сечения балки, отстоящей на расстоянии y от нейтральной оси x:
, возникающих в произвольной точке поперечного сечения балки, отстоящей на расстоянии y от нейтральной оси x:
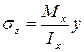 . (7.5)
. (7.5)
Отметим, что в формулу (7.5), которая, кстати, впервые была получена Навье, следует подставлять абсолютные значения изгибающего момента 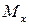 и координаты y. Будет ли напряжение в данной точке растягивающим или же сжимающим легко установить по характеру изгиба балки или, что является тем же самым, по эпюре изгибающих моментов, ординаты которой откладываются нами со стороны сжатых волокон балки.
и координаты y. Будет ли напряжение в данной точке растягивающим или же сжимающим легко установить по характеру изгиба балки или, что является тем же самым, по эпюре изгибающих моментов, ординаты которой откладываются нами со стороны сжатых волокон балки.
Из формулы (7.5) видно, что нормальные напряжения 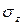 изменяются по высоте поперечного сечения балки по линейному закону.
изменяются по высоте поперечного сечения балки по линейному закону.
Напомним, что по ширине сечения они считаются постоянными.
На рис. 7.8, в показана эпюра нормальных напряжений. Наибольшие напряжения при изгибе балки возникают в точках, наиболее удаленных от нейтральной оси.
Несложный анализ эпюры нормальных напряжений показывает, что при изгибе балки материал, расположенный вблизи нейтральной оси, практически не работает. Поэтому в целях снижения веса балки рекомендуется выбирать такие формы поперечного сечения, у которых большая часть материала удалена от нейтральной оси как, например, у двутаврового
профиля.
7.23. Не совсем понятно, в каком месте при выводе формулы для нормальных напряжений мы воспользовались принятым ранее допущением о том, что при изгибе продольные волокна балки не надавливают друг на друга?
Мы привели вывод формулы для нормальных напряжений таким, каким он дается практически во всех учебниках по сопротивлению материалов. И действительно, если в этом выводе, не сделать дополнительных комментариев, то будет не совсем ясно, в каком месте мы воспользовались упомянутым допущением.
Приоткроем занавес. Выше мы установили, что при изгибе балки имеет место продольная деформация волокон 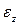 . При наличии надавливания продольных волокон, то есть при наличии нормального напряжения
. При наличии надавливания продольных волокон, то есть при наличии нормального напряжения  , продольная деформация должна измениться на слагаемое
, продольная деформация должна измениться на слагаемое
 ,
,
обусловленное влиянием коэффициента Пуассона 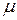 . Тогда
. Тогда
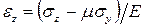 .
.
По аналогии поперечная деформация, связанная с изменением высоты поперечного сечения стержня, будет равна
 .
.
Из двух последних формул легко получить выражения для нормальных напряжений, возникающих в продольном и в поперечном направлениях балки:
 .
.
Эти формулы представляют собой обобщенный закон Гука для случая плоского напряженного состояния.
Принимая допущение о том, что продольные волокна балки не надавливают друг на друга, мы существенно упрощаем вывод формулы для нормальных напряжений 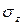 . Полагая, что
. Полагая, что 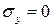 , мы из второй формулы обобщенного закона Гука находим:
, мы из второй формулы обобщенного закона Гука находим:

или
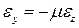 .
.
Тогда
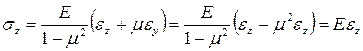 .
.
Полученное выражение и фигурирует у нас выше в формуле (7.2).
7.24. Что называется осевым моментом сопротивления при изгибе?
В том случае, когда поперечное сечение балки симметрично относительно нейтральной оси, нормальные напряжения в точках, наиболее удаленных от нее (при  ), определяются по формуле
), определяются по формуле
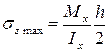 .
.
Геометрическую характеристику поперечного сечения балки, равную
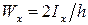 ,
,
и называют осевым моментом сопротивления при изгибе. Он измеряется в единицах длины в кубе (как правило, в см3).
Тогда наибольшие нормальные напряжения равны
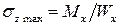 . (7.6)
. (7.6)
Заметим, что формула (7.6) по внешнему виду напоминает формулу (5.9) для наибольших касательных напряжений при кручении стержня. И здесь буквенное обозначение W, выбранное для обозначения осевого момента сопротивления при изгибе, очень похоже на перевернутую букву M, что также способствует лучшему запоминанию очень важной формулы (7.6).
