Вычисление обратной матрицы

Что такое обратная матрица? Прежде определим единичную матрицу.

Определение: Единичной матрицей n-го порядка называется такая матрица E_n, что для любой квадратной матрицы n-го порядка A_n выполняется соотношение

.

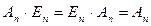Можно показать, что у единичной матрицы на главной диагонали расположены единицы, а все остальные элементы равны нулю.

Определение: Обратной матрицей для матрицы A_n с неравным нулю определителем (|A_n|¹0) называется такая матрица A_n^-1, для которой выполняется соотношение

.

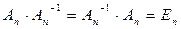Что необходимо знать и уметь для успешного изучения данного материала? Ответ. Вы должны уметь вычислять определители. Вы должны понимать, что такое матрица и уметь выполнять некоторые операции с матрицами.

Обратную матрицу A^-1можно найти по следующей формуле:

где |A| – определитель матрицы A, Ã – матрица алгебраических дополнений исходной матрицы, а Ã^T – присоединённая матрица, или транспонированная матрица алгебраических дополнений соответствующих элементов матрицы A.

(Обозначение Ã читаем «A с тильдой»)

Понятие обратной матрицы, как и понятие определителя, существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.

Обозначения:Как Вы уже, наверное, заметили, обратная матрица обозначается добавлением надстрочного индекса (^-1) к символу исходной матрицы.

Начнем с простейшего случая – матрицы «два на два». Чаще, конечно, требуется найти обратную матрицу для матрицы «три на три», но мы настоятельно рекомендуем изучить более простое задание, чтобы усвоить общий принцип решения.

Пример:

Найти обратную матрицу для матрицы .

Решаем. Последовательность действий удобно разложить по пунктам.

1) Сначала находим определитель матрицы.

.

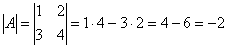Важно! У матрицы, определитель которой равен НУЛЮ, обратной матрицы НЕ СУЩЕСТВУЕТ (Это следствие из основной теоремы об обратной матрице).

В рассматриваемом примере, как выяснилось, |A| = -2 ¹ 0, а значит, всё в порядке.

2) Находим матрицу миноров элементов.

Матрица миноров элементов имеет такие же размеры, как и матрица A, то есть, в данном случае,

.

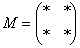Дело за малым, осталось найти четыре числа и поставить их вместо звездочек.

Возвращаемся к нашей матрице . Сначала рассмотрим левый верхний элемент

.

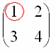Как найти минор этого элемента матрицы?

А делается это так: МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент:

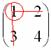
Оставшееся число в данном случае и является минором данного элемента, которое записываем в нашу матрицу миноров:

Рассматриваем следующий элемент матрицы :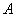

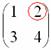
Мысленно вычеркиваем строку и столбец, в котором стоит данный элемент:

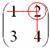
То, что осталось, и есть минор данного элемента, который записываем в нашу матрицу:

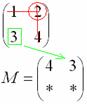
Аналогично рассматриваем элементы второй строки и находим их миноры:

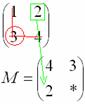
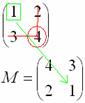
Готово.

– это и есть матрица миноровсоответствующих элементов матрицы A.

3) Находим матрицу алгебраических дополнений соответствующих элементов.

Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел:

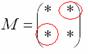. Именно у тех чисел, которые обведены в кружок! Получим:

- это матрица Ã алгебраических дополнений соответствующих элементов матрицы A.

4) Находим транспонированную матрицу алгебраических дополнений.

- это транспонированная матрица алгебраических дополнений соответствующих элементов матрицы A.

Ответ.

Вспоминаем нашу формулу

Всё найдено!

Таким образом, искомая обратная матрица: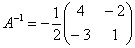

Ответ лучше оставить в таком виде. НЕ НУЖНОделить каждый элемент матрицы на 2, так как получатся дробные числа.

Как проверить решение? По определению обратной матрицы, необходимо выполнить матричное умножение 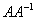либо .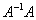

6) Проверка:

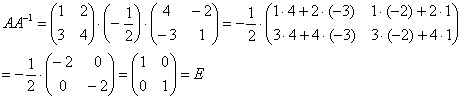
Получена так называемая единичная матрица(с единицами по главной диагонали и нулями в остальных местах). Таким образом, обратная матрица найдена правильно.

Перейдём к более распространенному на практике случаю – матрице «три на три».

Пример:

Найти обратную матрицу для матрицы

.

Алгоритм точно такой же, как и для случая «два на два».

Обратную матрицу найдем по формуле: , где 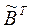– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы B.