Метод вариации произвольных постоянных. Примеры решений

Метод вариации произвольных постоянных применяется для решения неоднородных дифференциальных уравнений. Данный урок предназначен для тех студентов, кто уже более или менее хорошо ориентируется в теме. Если вы только-только начинаете знакомиться с ДУ, т.е. являетесь чайником, то рекомендую начать с первого урока: Дифференциальные уравнения первого порядка. Примеры решений. А если уже-уже заканчиваете, пожалуйста, отбросьте возможное предвзятое мнение, что метод сложный. Потому что он простой.

В каких случаях применяется метод вариации произвольных постоянных?

1) Метод вариации произвольной постояннОЙ можно использовать при решении линейного неоднородного ДУ 1-го порядка. Коль скоро уравнение первого порядка, то и постоянная (константа) тоже одна.

2) Метод вариации произвольнЫХ постоянных используют для решения некоторых линейных неоднородных уравнений второго порядка. Здесь варьируются две постоянные (константы).

Логично предположить, что урок будет состоять из двух параграфов…. Вот написал это предложение, и минут 10 мучительно думал, какую бы еще умную хрень добавить для плавного перехода к практическим примерам. Но почему-то мыслей после праздников нет никаких, хотя вроде и не злоупотреблял ничем. Поэтому сразу примемся за первый параграф.

Метод вариации произвольной постоянной
для линейного неоднородного уравнения первого порядка

Перед рассмотрением метода вариации произвольной постоянной желательно быть знакомым со статьей Линейные дифференциальные уравнения первого порядка. На том уроке мы отрабатывали первый способ решения неоднородного ДУ 1-го порядка. Этот первый способ решения, напоминаю, называется метод замены или метод Бернулли (не путать с уравнением Бернулли!!!)

Сейчас мы рассмотрим второй способ решения – метод вариации произвольной постоянной. Я приведу всего три примера, причем возьму их из вышеупомянутого урока Линейные неоднородные ДУ 1-го порядка. Почему так мало? Потому что на самом деле решение вторым способом будет очень похоже на решение первым способом. Кроме того, по моим наблюдениям, метод вариации произвольных постоянных применяется реже метода замены.

Пример 1

Найти общее решение дифференциального уравнения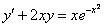
(Диффур из Примера №2 урока Линейные неоднородные ДУ 1-го порядка)

Решение: Данное уравнение является линейным неоднородным и имеет знакомый вид:

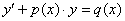
На первом этапе необходимо решить более простое уравнение:
То есть, тупо обнуляем правую часть – вместо 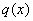пишем ноль.
Уравнение я буду называть вспомогательным уравнением.

В данном примере нужно решить следующее вспомогательное уравнение:

Перед нами уравнение с разделяющимися переменными, решение которого (надеюсь) уже не представляет для вас сложностей:

Таким образом:
– общее решение вспомогательного уравнения .

На втором шаге заменим константу 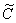некоторой пока ещё неизвестной функцией 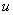, которая зависит от «икс»:

Отсюда и название метода – варьируем константу 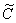. Как вариант, константа 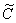может быть некоторой функцией 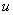, которую нам предстоит сейчас найти.

В исходном неоднородном уравнении 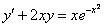проведём замену:

По правилу дифференцирования произведения:

Подставим и в уравнение :

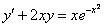Контрольный момент – два слагаемых в левой части сокращаются. Если этого не происходит, следует искать ошибку выше.

В результате замены получено уравнение с разделяющимися переменными. Разделяем переменные и интегрируем.

Какая благодать, экспоненты тоже сокращаются:

К найденной функции 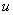приплюсовываем «нормальную» константу :

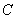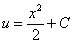
На заключительном этапе вспоминаем про нашу замену:

Функция 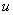только что найдена!

Таким образом, общее решение:

Ответ: общее решение:

Если вы распечатаете два способа решения, то легко заметите, что в обоих случаях мы находили одни и те же интегралы. Отличие лишь в алгоритме решения.

Теперь что-нибудь посложнее, второй пример я тоже прокомментирую:

Пример 2

Найти общее решение дифференциального уравнения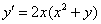
(Диффур из Примера №8 урока Линейные неоднородные ДУ 1-го порядка)

Решение: Приведем уравнение к виду :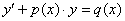

Обнулим правую часть и решим вспомогательное уравнение:

Разделяем переменные и интегрируем:

Общее решение вспомогательного уравнения:

В неоднородном уравнении проведём замену:

По правилу дифференцирования произведения:

Подставим и в исходное неоднородное уравнение :

Два слагаемых в левой части сокращаются, значит, мы на верном пути:

Интегрируем по частям. Вкусная буква 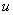из формулы интегрирования по частям у нас уже задействована в решении, поэтому используем, например, буквы «а» и «бэ»:

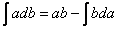
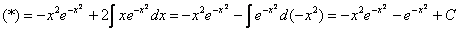
В итоге:

Теперь вспоминаем проведённую замену:

Ответ: общее решение: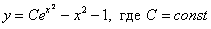

И один пример для самостоятельного решения:

Пример 3

Найти частное решение дифференциального уравнения, соответствующее заданному начальному условию.

,
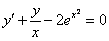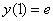
(Диффур из Примера №4 урока Линейные неоднородные ДУ 1-го порядка)
Решение:
Данное ДУ является линейным неоднородным. Используем метод вариации произвольных постоянных. Решим вспомогательное уравнение:

Разделяем переменные и интегрируем:

Общее решение:
В неоднородном уравнении проведем замену:

Выполним подстановку:

Таким образом, общее решение:

Найдем частное решение, соответствующее заданному начальному условию:

Ответ: частное решение:

Решение в конце урока может служить примерным образцом для чистового оформления задания.

Метод вариации произвольных постоянных
для линейного неоднородного уравнения второго порядка
с постоянными коэффициентами

Часто приходилось слышать мнение, что метод вариации произвольных постоянных для уравнения второго порядка – штука не из легких. Но я предполагаю следующее: скорее всего, метод многим кажется трудным, поскольку встречается не так часто. А в действительности особых сложностей нет – ход решения чёткий, прозрачный, понятный. И красивый.

Для освоения метода желательно уметь решать неоднородные уравнения второго порядка способом подбора частного решения по виду правой части. Данный способ подробно рассмотрен в статье Неоднородные ДУ 2-го порядка. Вспоминаем, что линейное неоднородное уравнение второго порядка с постоянными коэффициентами имеет вид:

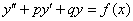
Метод подбора, который рассматривался на вышеупомянутом уроке, проходит лишь в ограниченном ряде случаев, когда в правой части 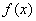находятся многочлены, экспоненты, синусы, косинусы. Но что делать, когда справа, например, дробь, логарифм, тангенс? В такой ситуации на помощь как раз и приходит метод вариации постоянных.

Пример 4

Найти общее решение дифференциального уравнения второго порядка

Решение: В правой части данного уравнения находится дробь, поэтому сразу можно сказать, что метод подбора частного решения не прокатывает. Используем метод вариации произвольных постоянных.

Ничто не предвещает грозы, начало решения совершенно обычное:

Найдем общее решение соответствующего однородного уравнения:

Составим и решим характеристическое уравнение:


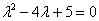
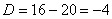
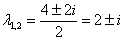– получены сопряженные комплексные корни, поэтому общее решение:

Обратите внимание на запись общего решения 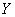– если есть скобки, то их раскрываем.

Теперь проделываем практически тот же трюк, что и для уравнения первого порядка: варьируем константы , заменяя их неизвестными функциями . То есть, общее решение неоднородногоуравнения будем искать в виде:

, где – пока ещё неизвестные функции.

Далее необходимо решить систему двух уравнений с двумя неизвестными:

Похоже на свалку бытовых отходов, но сейчас всё рассортируем.

В качестве неизвестных выступают производные функций . Наша цель – найти производные , причем найденные производные должны удовлетворять и первому и второму уравнению системы.

Откуда берутся «игреки»? Их приносит аист. Смотрим на полученное ранее общее решение и записываем:

,

Найдем производные:

С левыми частями разобрались. Что справа?

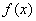– это правая часть исходного уравнения, в данном случае:

Коэффициент – это коэффициент при второй производной:

На практике почти всегда , и наш пример не исключение.

Всё прояснилось, теперь можно составить систему:

Систему обычно решают по формулам Крамера, используя стандартный алгоритм. Единственное отличие состоит в том, что вместо чисел у нас функции.

Найдем главный определитель системы:

Если позабылось, как раскрывается определитель «два на два», обратитесь к уроку Как вычислить определитель? Ссылка ведёт на доску позора =)

Итак: , значит, система имеет единственное решение.

Едем дальше:

Находим производную:

Но это еще не всё, пока мы нашли только производную.
Сама функция восстанавливается интегрированием:

Здесь добавляем «нормальную» константу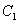

Разбираемся со второй функцией:

Здесь добавляем «нормальную» константу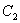

На заключительном этапе решения вспоминаем, в каком виде мы искали общее решение неоднородного уравнения? В таком:

Нужные функции только что найдены!

Осталось выполнить подстановку и записать ответ:

Ответ: общее решение:

В принципе, в ответе можно было раскрыть скобки.

Полная проверка ответа выполняется по стандартной схеме, которая рассматривалась на уроке Неоднородные ДУ 2-го порядка. Но проверка будет непростой, поскольку предстоит находить достаточно тяжелые производные и проводить громоздкую подстановку. Это неприятная особенность, когда вы решаете подобные диффуры.

Пример 5

Решить дифференциальное уравнение методом вариации произвольных постоянных

Это пример для самостоятельного решения. На самом деле в правой части тоже дробь. Вспоминаем тригонометрическую формулу , её, к слову, нужно будет применить по ходу решения.

Метод вариации произвольных постоянных – наиболее универсальный метод. Им можно решить любое уравнение, которое решается методом подбора частного решения по виду правой части. Возникает вопрос, а почему бы и там не использовать метод вариации произвольных постоянных? Ответ очевиден: подбор частного решения, который рассматривался на уроке Неоднородные уравнения второго порядка, значительно ускоряет решение и сокращает запись – никакого трахча с определителями и интегралами.

Рассмотрим два примера с задачей Коши.

Пример 6

Найти частное решение дифференциального уравнения, соответствующее заданным начальным условиям

,

Решение: Опять дробь и экспонента в интересном месте.
Используем метод вариации произвольных постоянных.

Найдем общее решение соответствующего однородного уравнения:



– получены различные действительные корни, поэтому общее решение:

Общее решение неоднородного уравнения ищем в виде: , где – пока ещё неизвестные функции.

Составим систему:

В данном случае:
,
Находим производные:
,

Таким образом:

Систему решим по формулам Крамера:
, значит, система имеет единственное решение.

Восстанавливаем функцию интегрированием:

Здесь использован метод подведения функции под знак дифференциала.

Восстанавливаем вторую функцию интегрированием:

Такой интеграл решается методом замены переменной:

Из самой замены выражаем:

Таким образом:

Данный интеграл можно найти методом выделения полного квадрата, но в примерах с диффурами я предпочитаю раскладывать дробь методом неопределенных коэффициентов:

Обе функции найдены:

В результате, общее решение неоднородного уравнения:

Найдем частное решение, удовлетворяющее начальным условиям .

Технически поиск решения осуществляется стандартным способом, который рассматривался в статье Неоднородные дифференциальные уравнения второго порядка.

Держитесь, сейчас будем находить производную от найденного общего решения:

Вот такое вот безобразие. Упрощать его не обязательно, легче сразу составить систему уравнений. В соответствии с начальными условиями :

Подставим найденные значения констант в общее решение:

В ответе логарифмы можно немного запаковать.

Ответ: частное решение:

Как видите, трудности могут возникнуть в интегралах и производных, но никак не в самом алгоритме метода вариации произвольных постоянных. Это не я вас запугал, это всё сборник Кузнецова!

Для расслабления заключительный, более простой пример для самостоятельного решения:

Пример 7

Решить задачу Коши

,

Пример несложный, но творческий, когда составите систему, внимательно на неё посмотрите, прежде чем решать ;-)

Конец.

Желаю успехов!

Решения и ответы:

Пример 3: Решение:
Данное ДУ является линейным неоднородным. Используем метод вариации произвольных постоянных. Решим вспомогательное уравнение:

Разделяем переменные и интегрируем:

Общее решение:
В неоднородном уравнении проведем замену:

Выполним подстановку:

Таким образом, общее решение:

Найдем частное решение, соответствующее заданному начальному условию:

Ответ: частное решение:

Пример 5: Решение: Используем метод вариации произвольных постоянных.
Найдем общее решение соответствующего однородного уравнения:

– сопряженные комплексные корни, поэтому общее решение: .
Общее решение неоднородного уравнения ищем в виде:
Составим систему:

В данном случае:
,
, ,


Таким образом:

Систему решим по формулам Крамера:
, значит, система имеет единственное решение.






В результате:

Ответ: общее решение:

Пример 7: Решение: Используем метод вариации произвольных постоянных.
Найдем общее решение соответствующего однородного уравнения:



– кратные действительные корни, поэтому общее решение:
.
Общее решение неоднородного уравнения ищем в виде:
Составим систему:

В данном случае:
,
,


Таким образом:

Кто-то будет мучиться с экспонентами, но счастье – вовремя заметить, что каждое уравнение можно сократить на !

Систему решим по формулам Крамера:
, значит, система имеет единственное решение.






В результате общее решение:

Найдем частное решение, соответствующее начальным условиям .


Подставим найденные значения констант в общее решение:

Ответ: частное решение: