Классические вероятности. Формулы комбинаторики

Рассматриваемое вероятностное пространство исторически является первой попыткой придать теории вероятности числовой, математический, характер. Она принадлежит Лапласу и часто называется моделью Лапласа. В этой модели все элементарные события равновероятны - ни у одного из них нет преимуществ появиться в опыте по сравнению с другими.

Например, в урне имеется неотличимые на ощупь шары черного и красного цвета. У каждого шара имеется одинаковая вероятность быть извлечённым из урны. В связи с этим классические вероятности называют еще « схемой урн» или « схемой случаев».

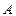Итак, имеется конечное пространство элементарных событий . Некоторому событию в рамках этого опыта благоприятствуют, например, элементарные события (случаи): 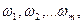т.е. появление этих случаев означает появление события 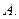Поскольку случаи равновероятны, то вероятность определяется лишь их числом, поэтому классическое определение вероятности даётся формулой:

.

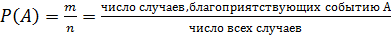Пример 10. В урне имеется 10 шаров - 3 белых, 2 черных, 5 красных. Наугад вынимается шар. Какова вероятность того, что он белый.

Это простейшая задача - всего шаров 10, из них событию (вынимается белый шар) благоприятствуют 3 шара (в урне 3 белых шара), поэтому

Однако не все задачи столь просты. Даже в примере 10 можно ставить более сложные вопросы. Например, пусть извлекаются 3 шара. Какова вероятность, что все они белые?, или какова вероятность того, что все они разного цвета? и т.п. Ответы на эти вопросы уже требуют размышлений. Чтобы облегчить их, приводим необходимые в таких случаях формулы комбинаторики.

В модели Лапласа имеется некоторое множество элементов, из которых извлекаются различные подмножества, они называются комбинациями. Комбинации составляются по-разному - с возвращением извлекаемых элементов или без возвращения; учитывая очередность извлечения или нет и т.д.

Рассмотрим основные формулы.

1) Основная формула комбинаторики (правило произведения)

Пусть имеется 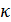множеств элементов

1 2 k

…………………

a b … c

Рис.6

Пусть в 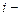м множестве содержится элементов, Будем составлять комбинации по одному элементу из каждого множества (рис.6). Тогда общее число 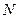различных комбинаций определяется основной формулой комбинаторики:

N= 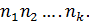(2)

Пример 11. Найти число всех различных трехзначных чисел с различными цифрами.

Решение. Рассуждаем так: число всех цифр равно десяти – 0,1,2,…9. В нашей задаче имеется три 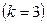множества цифр для 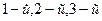цифр трехзначного числа. При этом первой цифрой числа может быть любая ненулевая - имеется 9 возможностей: 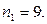Второй цифрой числа может быть любая цифра, отличная от первой цифры числа, в том числе и нуль. Следовательно, вторую цифру числа можно выбрать также девятью способами 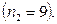Наконец, к каждой паре первых двух цифр числа надо добавить третью цифру, причем отличную от первых двух. Для этого есть 8 возможностей Следовательно, число всех различных трехзначных чисел с разными цифрами равно (рис.17).

1 0 2

1 0 3

1 0 4

9 8 7

Рис.7

Заметим, что если все 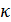множеств содержат одинаковое число элементов то

(3)

при этом можно считать, что комбинации составляются из одного множества, содержащего n различных элементов, причём каждый извлечённый элемент фиксируется и возвращается обратно в множество. Такая процедура называется выбором с возвращением, число всех выборок из элементов по элементов в каждой выборке (произносят: число всех выборок с возвращением « из эн по ка») вычисляется по формуле (3).

Пример 12. Сколько можно составить различных трёхзначных чисел, используя цифры от 1 до 9.

Ответ:

В частности, используя цифры 1,2 (n = 2) можно составить трёхзначных чисел 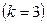в количестве Перечислим их:

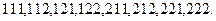
Рассмотрим теперь выборки без возвращения.

Пусть имеется множество, содержащее различных элементов: Из этой совокупности извлекаются элементы и располагаются в порядке извлечения, т.е. порядок фиксируется. В каждой такой комбинации находится элементов. Таким образом, составляются комбинации, состоящие из элементов, причём комбинации отличаются либо набором элементов, либо порядком. Такие комбинации называется размещениями из элементов по элементов в каждой комбинации 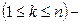читается: «размещения из 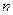по 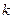». 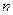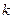Число всех размещений из по обозначается и легко получается из основной формулы комбинаторики:

(4)

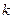сомножителей

Напомним о договорённости считать 0! = 1.

Пример 13. Составим все размещения из трех элементов по два: Как видим, их штук.

Нетрудно видеть, что если из 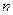элементов составлять размещения по 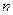элементов, то отличаться они будут лишь порядком их разположения в каждой комбинации, поэтому они называются перестановками из 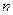элементов. Число всех перестановок из 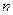элементов обозначается Из формулы (4) ясно, что

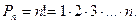(5)

Наконец, рассмотрим еще один способ составления комбинаций из 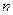элемент ов по когда порядок следования элементов не учитывается. Такие комбинации называются сочетаниями из 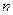элементов по Следовательно, сочетания различаются лишь набором элементов. Ясно, что число сочетаний меньше, чем число размещений, поскольку для того, чтобы из каждого сочетания «из 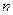по 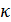» получить размещения, надо 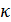входящих в него элемента переставить местами, а сделать это можно 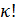способами. 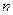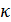Число сочетаний «из по » обозначается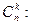

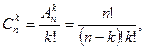
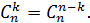(6)

Пример 14. В урне находятся 3 белых, 2 черных и 5 красных шаров. Из урны наугад извлекают 3 шара. Найти вероятности событий: 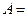(все три шара – красные); (2 шара красные, один белый), 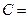(все три шара разного цвета).

Решение. Перед нами схема Лапласа, следовательно, вероятность каждый раз будем вычислять по классическому определению.

1)

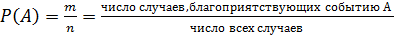
Каждый раз делается выборка из 10 шаров по 3 шара в каждой комбинации. Ясно, что порядок извлечения шаров роли не играет, т.е. составляются сочетания из 10 элементов (шаров) по три элемента. Таким образом, Из этих 120 комбинаций надо выбрать благоприятствующие событию 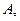т.е. содержащие 3 красных шара. Всего в урне 5 красных шаров и только из них можно получать «благоприятствующие» комбинации-всего таких комбинаций Таким образом,

2) Как и в первом случае Вычисляем два красных шара можно извлечь десятью способами, а один белый 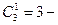тремя способами. По основной формуле комбинаторики поэтому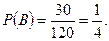

3) Вычисление Р(С) проведем без комментариев - читатель, надеемся, без труда поймёт выкладки: следовательно,