Модели стационарных и нестационарных временных рядов и их идентификация

Набор случайных переменных X(t), где 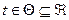(вещественные числа) называется стохастическим процессом. Дискретный стохастический процесс определяется как последовательность случайных переменных X(t), где t = t₁, t₂, ..., t_T или короче Х₁, Х₂,..., Х_Т..., или просто X_t.

Математическое ожидание E(X_t) может изменяться во времени и представляет собой функцию среднего в зависимости от времени

.

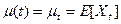Аналогичным образом дисперсия (X_t) является функцией, также зависящей от времени:

.

В общем случае в каждый момент времени существует определенная дисперсия. Это не то же самое, что изменчивость эмпирических данных по мере развития процесса во времени.

Автоковариация

в общем виде зависит от каждого t₁ и t₂.

Конечная реализация x₁, х₂,..., х_т дискретного стохастического процесса ... Х₁, Х₂,... Х_т... называется временным рядом.

Рассмотрим различие между стохастическим процессом и сгенерированным им временным рядом.

Процессы обозначаются прописными буквами, обозначают временные ряды строчными буквами. Исключениями являются остатки в моделях стохастических процессов, не имеющие никакой самостоятельной практической значимости. Они также обозначаются строчными буквами, например а, и и ε. Строгое разграничение необходимо для корректного вывода свойств временных рядов из свойств стохастических процессов. Позднее при моделировании реальных временных рядов это условие можно будет ослабить или опустить.

Стохастический процесс X_t называется стационарным в сильном смысле, если совместное распределение вероятностей всех переменных точно то же самое, что и для переменных .

Под стационарным процессом в слабом смысле понимается стохастический процесс, для которого среднее и дисперсия независимо от рассматриваемого периода времени имеют постоянное значение, а автоковариация зависит только от длины лага между рассматриваемыми переменными.

Среднее ……………. .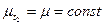

Дисперсия …………. .

Автоковариация …… ,

где 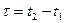(лаг).

Автоковариация как функция длины лага τ

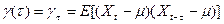
называется автоковариационной функцией. При τ = 0 ее значение равно дисперсии.

Проведя нормировку 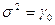, получим автокорреляционную функцию стационарного стохастического процесса:

,

где .

Временной ряд х₁, х₂, ..., х_Т, т. е. конкретная реализация стационарного стохастического процесса X_t также называется стационарным.

В практической аналитической работе стационарность временного ряда означает отсутствие:

• тренда;

• систематических изменений дисперсии;

• строго периодичных флуктуаций;

• систематически изменяющихся взаимозависимостей между элементами временного ряда.

Экономические временные ряды представляют собой данные наблюдений за экономическими показателями, например, валовым внутренним продуктом, за ряд лет, и такие ряды, как правило, нестационарны.

Графическое представление стационарного ряда

Эргодичность

Основная проблема в оценивании параметров распределения стохастического процесса состоит в том, что в общем случае размер выборки n = 1, поскольку обычно имеется единственная реализация процесса. Ввиду этого сделать осмысленную оценку практически невозможно. Изучаемый стохастический процесс как таковой неизвестен. Его стационарность или нестационарность может быть установлена только посредством анализа соответствующего ему временного ряда. Но, с другой стороны, многие методы анализа временных рядов предполагают их стационарность. Это приводит к своего рода замкнутому кругу, когда свойство, на наличие которого проводится исследование, входит в изначальные предпосылки.

Данную проблему можно решить с использованием понятия эргодичность: это поведение большого класса стационарных процессов, когда арифметическое среднее со временем сходится к математическому ожиданию μ. Эргодичность делает возможным оценивание стохастического процесса только по его реализации - временному ряду.

Известны различные подходы к распознаванию стационарности временных рядов:

· графическое представление временного ряда и визуальная проверка на наличие какого-либо тренда, т.е. меняющегося среднего, увеличивающейся или уменьшающейся дисперсии, устойчивых периодичностей;

· исследование на наличие автокорреляции в реальных данных;

· тесты на присутствие детерминистического тренда, например t - тест на коэффициенты оценок метода наименьших квадратов;

· тесты на наличие стохастического тренда, например тесты на единичный корень.

Особые случаи

Процесс называется нормальным, если совместное распределение X_t1 , X_t2 ,..., X_tn - это n-мерное нормальное распределение. В данном случае из стационарности в слабом смысле следует стационарность в сильном смысле.

«Белым шумом» называется чисто случайный процесс, т.е. ряд независимых, одинаково распределенных случайных величин a_t (iid). Главные свойства «белого шума» следующие:

для .

Из этого очевидным образом следует стационарность. «Белый шум» играет важную роль при моделировании остатков или шоков стохастического процесса, генерирующего данные (временной ряд).

Для того чтобы проверить, является ли временной ряд x_t «белым шумом», можно протестировать его выборочную автокорреляцию 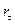с помощью Q-статистики Бокса - Пирса:

.

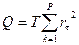При нулевой гипотезе о том, что X_t - «белый шум» Q-статистика имеет -распределение с р степенями свободы.