Тригонометрические неравенства
При решении простейших тригонометрических неравенств вида f (x) ≥ а, (либо f (x) > а, f (x) < а, f (x)  где f (x) − одна из тригонометрических функций, удобно использовать тригонометрическую окружность, которая позволяет наглядно представить решения неравенства и записать ответ.
где f (x) − одна из тригонометрических функций, удобно использовать тригонометрическую окружность, которая позволяет наглядно представить решения неравенства и записать ответ.
Пример 9. Решить неравенство 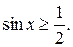
Δ Нарисуем тригонометрическую окружность и отметим на ней точки, для которых ордината не меньше числа  (см. рис. 1).
(см. рис. 1).
Для |
Для решения неравенств с тангенсом и котангенсом применяются линии тангенсов и котангенсов - прямые x = 1 и y = 1 соответственно, касающиеся тригонометрической окружности (см. рис. 2).
Легко заметить, что если построить луч с началом в начале координат, составляющий угол α с положительным направлением оси абсцисс, то длина отрезка от точки (1; 0) до точки пересечения этого луча с линией тангенсов в точности равна тангенсу угла, который составляет этот луч с осью абсцисс. Аналогичное наблюдение имеет место и для котангенса.
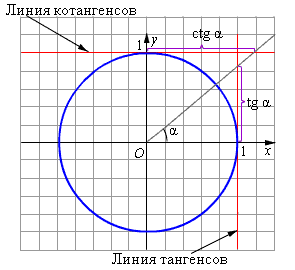
Рисунок 2
Пример 10. Решить неравенство 
Δ Обозначим 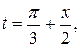 тогда неравенство примет вид простейшего:
тогда неравенство примет вид простейшего:  Рассмотрим интервал
Рассмотрим интервал  длины, равной π - основному периоду тангенса. На этом интервале с помощью линии тангенсов устанавливаем, что
длины, равной π - основному периоду тангенса. На этом интервале с помощью линии тангенсов устанавливаем, что  Вспоминаем теперь, что необходимо добавить
Вспоминаем теперь, что необходимо добавить 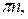
 поскольку основной период тангенса равен π. Итак,
поскольку основной период тангенса равен π. Итак, 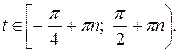 Возвращаясь к переменной x, получаем, что
Возвращаясь к переменной x, получаем, что



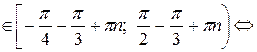


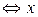

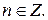
Ответ: 
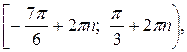
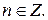
Для решения неравенств, содержащих обратные тригонометрические функции удобно пользоваться графиками этих функций (см. рис. 3-6).


Рисунок 3 Рисунок 4
Арксинус Арккосинус
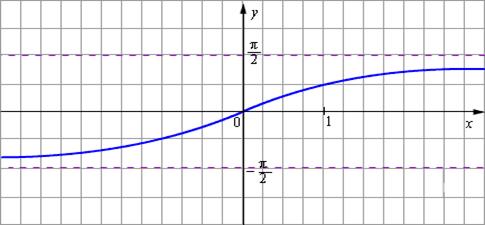
Рисунок 5 Арктангенс

Рисунок 6 Арккотангенс
Пример 11. Решить неравенство 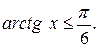
Δ Воспользуемся графиком функции 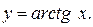 Найдём точку пересечения этого графика с горизонтальной прямой
Найдём точку пересечения этого графика с горизонтальной прямой  Это точка с абсциссой
Это точка с абсциссой 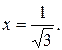 По графику видно (см. рис. 2), что для всех
По графику видно (см. рис. 2), что для всех 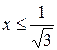 график функции лежит ниже прямой
график функции лежит ниже прямой  Следовательно, эти x и составляют решение данного неравенства. function changeDecision(proofobj, proofname) { if (proofobj.style.display=='none') { proofobj.style.display='inline'; proofname.innerHTML='Решение'; } else { proofobj.style.display='none'; proofname.innerHTML='Показать решение'; } }
Следовательно, эти x и составляют решение данного неравенства. function changeDecision(proofobj, proofname) { if (proofobj.style.display=='none') { proofobj.style.display='inline'; proofname.innerHTML='Решение'; } else { proofobj.style.display='none'; proofname.innerHTML='Показать решение'; } }
Ответ: 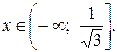
|
Учебная карта к занятию 8.
Задания уровня А
1.1 Решите уравнения: а)  б)
б) 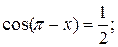 в)
в) 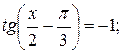
г)  д)
д) 
1.2 Решите неравенства: а) 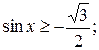 б)
б)  в)
в) 
г) 
Задания уровня В
2.1 Решите уравнения: а)  б)
б) 
2.2 Решите уравнения: а) 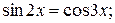 б)
б) 
в)  г)
г) 

Задания уровня С
3.1 Решите уравнение 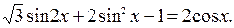
Домашнее задание
1.3 Решите уравнения: а)  б)
б) 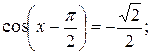
в)  г)
г)  д)
д) 
1.4 Решите неравенства: а) 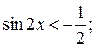 б)
б) 
в)  г)
г) 
2.3 Решите уравнения: а)  б)
б) 
2.4 Решите уравнения: а)  ,
,
б) 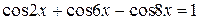 , в)
, в) 
Ответы и указания к заданиям
1.1 а)  б)
б) 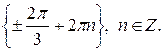 в)
в) 
г) 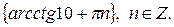 д)
д) 
1.2а) 
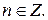 б)
б) 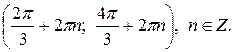
в) 
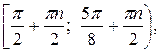
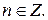 г)
г) 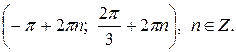
1.3 а)  б)
б)  в)
в) 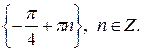
г) 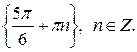 д)
д) 
1.4 а)  б)
б) 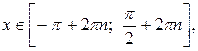
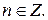
в)  г)
г) 

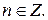
2.1 а) 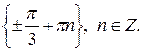 Указание. Перейти к равносильному уравнению
Указание. Перейти к равносильному уравнению
 , затем решить совокупность уравнений, объединив решения.
, затем решить совокупность уравнений, объединив решения.
б) 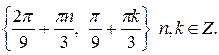
2.2а)  Указание. Воспользоваться формулой приведения
Указание. Воспользоваться формулой приведения  , а затем разложить на множители по формуле разности косинусов. б)
, а затем разложить на множители по формуле разности косинусов. б)  Указание. Воспользоваться методом введения вспомогательного угла.в)
Указание. Воспользоваться методом введения вспомогательного угла.в) 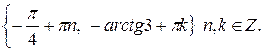 Указание. Приведите к однородному уравнению 2-ой степени, представив
Указание. Приведите к однородному уравнению 2-ой степени, представив  г)
г) 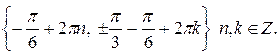
2.3 а)  б)
б) 
2.4а)  Указание. Перенесите 1 влево и разложите на множители, применив основное тригонометрическое тождество.
Указание. Перенесите 1 влево и разложите на множители, применив основное тригонометрическое тождество.
б) 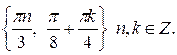 Указание. Перенесите вправо
Указание. Перенесите вправо  и сверните по формуле половинного угла, а левую часть разложите на множители по формуле суммы косинусов. В результате дальнейших преобразований получается три серии решений. Однако можно объединить две серии решений: 1)
и сверните по формуле половинного угла, а левую часть разложите на множители по формуле суммы косинусов. В результате дальнейших преобразований получается три серии решений. Однако можно объединить две серии решений: 1)  и заменить их одной:
и заменить их одной: 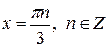 поскольку все точки второй серии решений содержатся в первой серии.
поскольку все точки второй серии решений содержатся в первой серии.
в)  3.1
3.1  Указание. Преобразовать левую часть уравнения с помощью метода вспомогательного угла, представив её в виде
Указание. Преобразовать левую часть уравнения с помощью метода вспомогательного угла, представив её в виде  Затем рассмотреть сумму косинусов и представив её в виде произведения, перейти к совокупности двух уравнений.
Затем рассмотреть сумму косинусов и представив её в виде произведения, перейти к совокупности двух уравнений.

 Рисунок 1
Рисунок 1  решением данного неравенства будут
решением данного неравенства будут 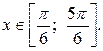 Ясно также, что если некоторое число x будет отличаться от какого-нибудь числа из указанного интервала на
Ясно также, что если некоторое число x будет отличаться от какого-нибудь числа из указанного интервала на  то sin x также будет не меньше
то sin x также будет не меньше  Следовательно, к концам найденного отрезка решения нужно просто добавить
Следовательно, к концам найденного отрезка решения нужно просто добавить 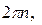 где
где 
 Рисунок 7
Рисунок 7