Статистическое изучение динамики

Задание 48. Имеются данные о численности безработных по Курганской области.

Показатель	2008 г.	2009 г.	2010 г.	2011 г.	2012 г.
Численность безработных, тыс. чел.	43,4	60,1	55,3	44,4	37,7

Рассчитайте и проанализируйте показатели ряда динамики.

Решение. Расчёт абсолютных и относительных показателей динамики проводится в таблице 27.

Таблица 27 – Динамика численности безработных по

Курганской области

Год	Численность безработных, тыс. чел.	Абсолютный прирост, тыс. чел.	Темп роста, %	Темп прироста, %	Абсолютное значение 1% прироста, тыс. чел.
базисный	цепной	базисный	цепной	базисный	цепной
		-	-	100,0	100,0	-	-	-

Расчёт средних показателей ряда динамики проводится по формулам:

Ÿ средний уровень ряда:

Ÿ средний абсолютный прирост

Ÿ средний темп роста:

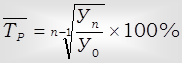
Ÿ средний темп прироста:

=

Вывод…..……………………………………………………………..…………….

…………………………………………………………………………………………….……………………………………………………………………………………………….………………………………………………………………………………………………….

& Задание 49. Имеются данные об объёмах производства сливочного масла в Курганской области.

Показатель	2008 г.	2009 г.	2010 г.	2011 г.	2012 г.
Производство сливочного масла, т

Рассчитайте и проанализируйте показатели ряда динамики.

Решение. Расчёт абсолютных и относительных показателей динамики проведём в таблице 28.

Таблица 28 – Динамика …

Год	Производство сливочного масла, т	Абсолютный прирост, т	Темп роста, %	Темп прироста, %	Абсолютное значение 1% прироста, т
базисный	цепной	базисный	цепной	базисный	цепной
		-	-	100,0	100,0	-	-	-

Расчёт средних показателей ряда динамики проведём по формулам:

· средний уровень ряда:

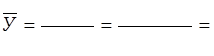
· средний абсолютный прирост

· средний темп роста:

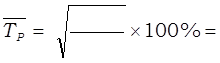
· средний темп прироста:

Вывод…..……………………………………………………………..…………….

…………………………………………………………………………………………….……………………………………………………………………………………………….………………………………………………………………………………………………….

Задание 50. Имеются следующие данные о годовом обороте розничной торговли. Проведите укрупнение периодов и выравнивание динамического ряда при помощи скользящей средней. Выявите основную тенденцию развития данного явления.

Год	Сумма, млн. р.
	16,6
	15,6
	17,9
	16,2
	17,9
	17,8
	18,5
	19,8
	19,1
	20,2
	21,8
	25,0

Решение. По данным об обороте розничной торговли проводится укрупнение периодов и выравнивание динамического ряда при помощи скользящей средней. Результаты расчётов приводятся в таблице 29.

Таблица 29 – Динамика оборота розничной торговли, млн. р.

Год	Сумма, млн. р.	Суммы по 3х-летиям	Средние по 3х-летиям	Суммы по скользящим 3х-летиям	Средние скользящие
	16,6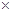
	15,6
	17,9
	16,2
	17,9
	17,8
	18,5
	19,8
	19,1
	20,2
	21,8
	25,0

Вывод…..……………………………………………………………..…………….

…………………………………………………………………………………………….……………………………………………………………………………………………….………………………………………………………………………………………………….

Задание 51. По данным задания 48 определите тенденцию изменения численности безработных в Курганской области, используя аналитическое выравнивание ряда динамики по уравнению прямой линии. Сформулируйте выводы.

Решение. Выравнивание по прямой линии проводится с помощью следующего уравнения:

,

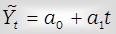где - параметры уравнения;

- порядковый номер года.

Для нахождения параметров уравнения прямой линии необходимо решить систему нормальных уравнений:

{ .

Для решения системы нормальных уравнений необходимо определить Для расчётов составляется таблица 30.

Система уравнений упрощается, так как .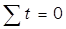

{ .

Таблица 30 – Аналитическое выравнивание численности безработных

в Курганской области по уравнению прямой

Год	Численность безработных, тыс. чел.	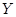Порядковый номер года	Расчётные данные
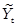		- 2
		- 1
ИТОГО

Отсюда а₀ и а₁ рассчитываются по формулам:

{

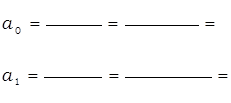
Уравнение линейного тренда имеет следующий вид:

Таким образом, ……………………………………………………………………….

…………………………………………………………………………………………….…………………………………………………………………………………………………………………………………………………………………………………………………

Подставляются в полученное уравнение значения t (из таблицы 30) и рассчитываются выровненные уровни численности безработных:

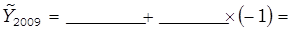
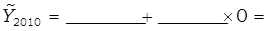
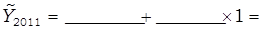
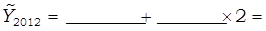
Изображаются фактические и выровненные уровни ряда динамики на графике:

– фактические уровни

– выровненные уровни

Рисунок 5 – Динамика численности безработных

в Курганской области

Вывод…..……………………………………………………………..…………….

…………………………………………………………………………………………….……………………………………………………………………………………………….………………………………………………………………………………………………….

& Задание 52. По данным задания 48 проведите аналитическое выравнивание ряда динамики численности безработных в Курганской области по уравнению параболы второго порядка. Сформулируйте выводы.

Решение. Проведём аналитическое выравнивание показателей ряда динамики по уравнению параболы второго порядка, с применением способа отсчёта от условного начала.

.

Для расчёта параметров этого уравнения необходимо определить 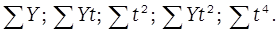Для расчётов составляется таблица 31.

Параметры уравнения параболы второго порядка определяются по формулам:

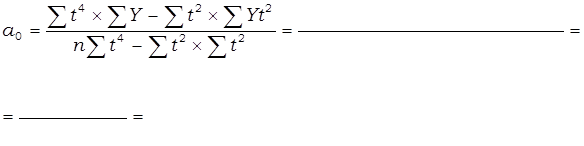
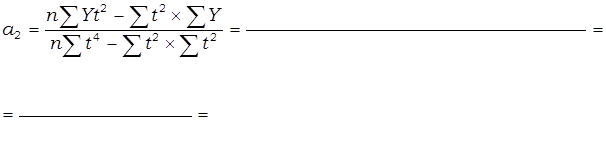
Таблица 31 – Аналитическое выравнивание численности безработных

в Курганской области по уравнению параболы

второго порядка

Год	Численность безработных, тыс. чел.	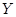Порядковый номер года	Расчётные данные
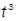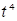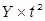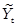ИТОГО

Таким образом, уравнение тренда примет следующий вид:

Подставляются в полученное уравнение значения t (из таблицы 31) и рассчитываются выровненные уровни численности безработных:

Изображаются фактические и выровненные уровни ряда динамики на графике:

– фактические уровни

– выровненные уровни

Рисунок 6 – Динамика численности безработных

в Курганской области

Вывод…..……………………………………………………………..…………….

…………………………………………………………………………………………….……………………………………………………………………………………………….………………………………………………………………………………………………….

Задание 53. По расчётам заданий 51 и 52 оцените степень приближения тренда к фактическим данным.

Решение. Рассчитывается среднее квадратическое отклонение, определённое по уравнениям прямой и параболы второго порядка.

Для расчётов составляется и заполняется таблица 32:

Таблица 32 – Данные для расчёта среднего квадратического отклонения

Год	Численность безработных, тыс. чел.	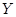По уравнению прямой	По уравнению параболы
выровненная численность безработных	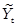	выровненная численность безработных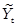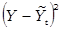
ИТОГО

По уравнению прямой:

По уравнению параболы:

Вывод…..……………………………………………………………..…………….

…………………………………………………………………………………………….…

……………………………………………………………………………………………………………………………………………………………………………………………….

Задание 54. Имеются следующие данные о средней яйценоскости одной курицы-несушки по месяцам за три года, штук.

Год

Месяц

I

II

III

IV

V

VI

VII

VIII

IX

X

XI

XII

Определите показатели сезонных колебаний средней яйценоскости одной курицы-несушки по данным среднемесячного уровня за три года. Изобразите графически изменения сезонных колебаний. Сформулируйте выводы.

Решение. Определяется средние значения уровней ряда для каждого месяца года, общий средний уровень яйценоскости одной курицы-несушки и индексы сезонности по каждому месяцу. Расчёты проводятся в таблице 33.

Таблица 33 – Расчёт индексов сезонности средней яйценоскости

одной курицы-несушки

Месяц	Средняя яйценоскость, шт.	Индекс сезонности, %
2010 г.	2011 г.	2012 г.
I
II
III
IV
V
VI
VII
VIII
IX
X
XI
XII

Общий уровень яйценоскости одной курицы-несушки в среднем по всей совокупности равен:

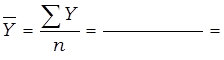
Изобразить полученные индексы сезонности в виде линейной диаграммы.

Рисунок 5 – Сезонные колебания яйценоскости кур-несушек

по месяцам

Вывод…..……………………………………………………………..…………….

…………………………………………………………………………………………….……………………………………………………………………………………………….………………………………………………………………………………………………….

Задание 55. По данным задания 48 рассчитайте эмпирические значения численности безработных в Курганской области с помощью линейной функции по уравнению прямой линии. Определите ожидаемую численность безработных на 2013 г., вероятностные границы, дайте интервальную оценку прогнозируемого явления. Сформулируйте выводы.

Решение. Составляется уравнение линейного тренда: . Для нахождения параметров этого уравнения необходимо решить систему уравнений:

{

Для решения системы уравнений необходимо определить Для расчётов составляется таблица 34 и решается система уравнений.

Таблица 38 – Динамика численности безработных в Курганской

области

Год	Численность безработных, тыс. чел.	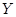Порядковый номер года	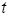Расчётные данные
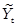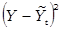ИТОГО

……….……………………

………………………….…

……….……………………

………………………….…

……….……………………

………………………….…

……….……………………

………………………….…

……….……………………

………………………….…

……….……………………

………………………….…

……….……………………

………………………….…

……….……………………

………………………….…

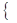Следовательно, уравнение линейного тренда имеет вид: ………………………………..

Подставляются в полученное уравнение значения t (из таблицы 38) и рассчитываются выровненные уровни численности безработных:

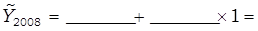
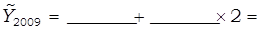
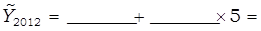
С помощью экстраполяции при 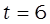необходимо определить ожидаемый уровень численности безработных в Курганской области в 2013 г.:

………………………………..=

Таким образом, ……………………………………………………………………

………………………………………………………………………………………….

Определяются границы интервалов прогнозируемого явления по формуле:

По данным приложения 3 определяется значение коэффициента доверия по распределению Стьюдента:

Остаточное среднее квадратическое отклонение равно:

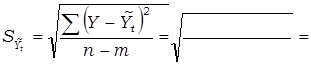
Тогда вероятностные границы интервала прогнозируемой численности безработных будут равны:

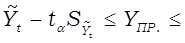
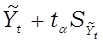
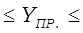
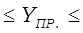
Вывод…..……………………………………………………………..…………….

…………………………………………………………………………………………….…

……………………………………………………………………………………………….

……………………………………………………………………………………………….

ИНДЕКСНЫЙ МЕТОД АНАЛИЗА

Задание 56. Имеются данные по ЗАО «Путь к коммунизму» Юргамышского района Курганской области. Рассчитайте индивидуальные индексы физического объёма продукции, себестоимости и цены.

Показатель	2010 г.	2012 г.
Объём продаж, ц
Себестоимость 1 ц, р.	1313,47	1605,00
Средняя цена реализации 1 ц, р.	1119,98	1581,29

Сформулируйте выводы.

Решение. Рассчитываются индивидуальные индексы.

Индивидуальный индекс физического объёма:

………………………………………………………………………………………………

………………………………………………………………………………………………

Индивидуальный индекс себестоимости:

………………………………………………………………………………………………

………………………………………………………………………………………………

Индивидуальный индекс средней цены:

………………………………………………………………………………………………

………………………………………………………………………………………………

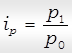
Задание 57. Имеются данные по ЗАО «Восток» Частоозерского района Курганской области. Определите изменение физического объёма продаж, средних цен реализации и выручки от продажи продукции.

Показатель	2010 г.	2012 г.
Реализовано скота в живой массе, ц: крупного рогатого скота
свиней
Средняя цена реализации, тыс. р.: крупного рогатого скота	3,98	7,67
свиней	6,65	4,15

Сформулируйте выводы.

Решение. Рассчитываются общие агрегатные индексы.

Общий агрегатный индекс физического объёма:

………………………………………………………………………………………………

………………………………………………………………………………………………

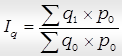
Общий агрегатный индекс средних цен реализации:

………………………………………………………………………………………………

………………………………………………………………………………………………

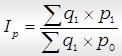
Общий агрегатный индекс выручки от продажи продукции:

или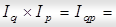

………………………………………………………………………………………………

………………………………………………………………………………………………

Задание 58. Имеются данные о реализации молока в двух сельскохозяйственных организациях Курганской области. Определите изменение суммы полученной выручки от продажи молока в целом и по факторам.

Показатель	2010 г.	2012 г.
Объём реализованного молока, ц: ЗАО «Глинки»
СПК «Племзавод «Разлив»
Средняя цена реализации 1 ц молока, р.: ЗАО «Глинки»	1783,40	1225,41
СПК «Племзавод «Разлив»	1755,36	2220,73

Сформулируйте выводы.

Решение. По исходной информации задания оформляется таблица 38.

Рассчитывается общее изменение выручки от продажи молока с помощью агрегатного индекса:

Определяется абсолютное изменение суммы выручки от продажи молока:

………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

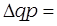
Таблица 38 – Показатели для индексного анализа

Предприятие	Объём реализованного молока, ц	Средняя цена реализации 1 ц молока, р.	Выручка от продажи молока, тыс. р.
2010 г.	2012 г.	2010 г.	2012 г.	2010 г.	2012 г.	усл.
Символ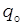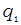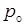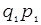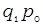
ЗАО «Глинки»
СПК «Племзавод «Разлив»
ИТОГО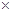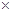

Рассчитывается влияние факторов на общее изменение выручки от продажи молока.

Ÿ за счёт изменения объёма реализации:

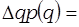
………………………………………………………………………………………………………………………………………………………………………………………………за счёт изменения средней цены реализации:

………………………………………………………………………………………………………………………………………………………………………………………………

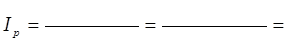
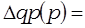
Проверка.

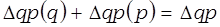
Задание 59. На основе данных, представленных в задании 58, определите влияние факторов на изменение средней цены реализации 1 ц молока. Сформулируйте выводы.

Решение. Рассчитывается уровень средней цены реализации молока по следующим формулам (данные см. в таблице 38):

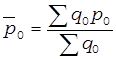
Рассчитывается общее изменение средней цены реализации с помощью индекса переменного состава:

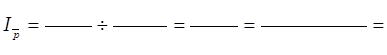
Определяется абсолютное изменение средней цены:

………………………………………………………………………………………………………………………………………………………………………………………………

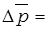
Рассчитывается влияние факторов на общее изменение уровня средней цены:

Ÿ за счёт изменения объёма и структуры реализации продукции (индекс структурных сдвигов):

………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

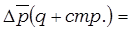
Ÿ за счёт изменения цены реализации молока по отдельным предприятиям (индекс постоянного состава):

………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Проверка.

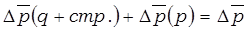
& Задание 60. Имеются данные о производстве и себестоимости зерна в СХПК «колхоз им. Свердлова» Шатровского района Курганской области. Определите изменение суммы затрат на производство зерна в целом и по факторам.

Показатель	2010 г.	2012 г.
Объём производства зерна, озимые зерновые
яровые зерновые
зернобобовые
Себестоимость единицы продукции, р.: озимые зерновые	228,49	331,57
яровые зерновые	324,06	383,06
зернобобовые	337,80	355,55

Сформулируйте выводы.

Решение. По исходной информации задания оформляется таблица 39.

Таблица 39 – Показатели для индексного анализа

Культура	Объём производства зерна, ц	Себестоимость единицы продукции, р.	Затраты на производство зерна, тыс. р.
2010 г.	2012 г.	2010 г.	2012 г.	2010 г.	2012 г.	усл.
Символ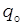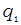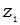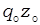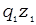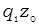
Озимые зерновые
Яровые зерновые
Зернобобовые
ИТОГО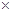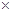

Рассчитаем общее изменение затрат на производство зерна с помощью агрегатного индекса:

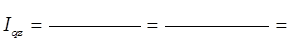
Определим абсолютное изменение суммы затрат на производство зерна:

………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Рассчитаем влияние факторов на общее изменение затрат на производство зерна:

Ÿ за счёт изменения объёма производства:

………………………………………………………………………………………………………………………………………………………………………………………………

· за счёт изменения себестоимости продукции:

………………………………………………………………………………………………………………………………………………………………………………………………

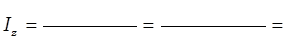
Проверка.

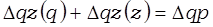
& Задание 61. На основе данных, представленных в задании 60, определите влияние факторов на изменение средней себестоимости 1 ц зерна. Сформулируйте выводы.

Решение. Рассчитаем уровень средней себестоимости зерна по следующим формулам (данные см. в таблице 39):

Рассчитаем общее изменение средней себестоимости зерна с помощью индекса переменного состава:

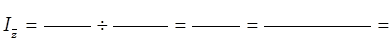
Определим абсолютное изменение средней себестоимости:

………………………………………………………………………………………………………………………………………………………………………………………………

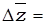
Рассчитаем влияние факторов на общее изменение уровня средней себестоимости:

Ÿ за счёт изменения объёма и структуры производства продукции (индекс структурных сдвигов):

………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

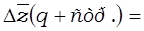
Ÿ за счёт изменения себестоимости зерна по отдельным культурам (индекс постоянного состава):

………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

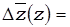
Проверка.