Второй закон термодинамики. Формулировка и формула

Тепло может передаваться от более нагретого к менее нагретому.
Все самопроизвольные процессы идут к равновесию.
Переход тепла от менее нагретого тела к более нагретому не может происходить самопроизвольно. Для осуществления такого процесса необходимо затратить работу.
S-энтропия.
dS>=q/T-------------

Соотношения, связывающие константу равновесия с) энергией Гиббса --------

(3.51)

есть величина, постоянная, называемая константой равновесия. Тогда

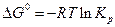, или

(3.52)

т. е. получаем соотношение для определения константы равновесия. При этом уравнение (3.50) принимает вид

(3.53)

и может быть использовано для анализа равновесия направления химических реакций.

Принцип Ле-Шателье -----------------------

если на систему, находящуюся в состоянии равновесия, оказывается внешнее воздействие, то в ней произойдут изменения, противодействующие этому. Пользуясь этим принципом и соотношением (3.53), можно через константу равновесия (3.51) управлять соотношением реагирующих веществ, т. е. в конечном итоге, выходом продуктов реакции.

Стадии гетерогенной реакции --------------------

В большинстве случаев гетерогенные реакции протекают через ряд стадий, наиболее характерные из которых следующие:

1) диффузия частиц исходных веществ к поверхности раздела фаз (реакционной зоне);

2) адсорбция реагентов на поверхности;

3) химическая реакция на поверхности;

4) десорбция продуктов реакции на поверхности раздела фаз;

5) диффузия этих продуктов от реакционной зоны вглубь одной из фаз.

Стадии 1 и 5 относятся к диффузионным, а стадии 2 – 4 к кинетическим.

Уравнение молекулярной диффузии и условия его применимости------------

Диффузия есть процесс самопроизвольного перемещения вещества, направленный на выравнивание концентраций в объеме. Движущейся силой диффузии является градиент концентрации , определяемый изменением концентрации вещества , приходящегося на отрезок пути 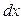в направлении диффузии. Приращение количества переносимого путем диффузии вещества пропорционально коэффициенту диффузии , градиенту концентрации, площади поперечного сечения 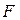среды, через которую переносится вещество, и времени

а переходя к бесконечно малым приращениям и скорости диффузии (потоку массы через единичную площадь) получаем уравнение 3.57

описывающее стационарную диффузию и называемое первым законом Фика.Для случая системы с распределенными параметрами, когда концентрация изменяется по всем трем координатам, в соответствии со вторым законом Фика уравнение диффузии принимает следующий вид:

(3.58)

где – плотность источников вещества, например, количество вещества, образующегося в результате химических реакций в единице объема в единицу времени.Необходимо подчеркнуть, что уравнения (3.57) и (3.58) относятся к молекулярному переносу в неподвижной среде и справедливы для изотермического процесса и случая, когда диффузия данного компонента не зависит от диффузии других компонентов.В этих условиях зависимость коэффициента диффузии от температуры 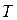, вязкости среды и радиуса диффундирующих молекул определяется формулой Стокса – Эйнштейна: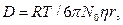

Уравнение турбулентной диффузии и его конкретный вид для диффузии кислорода из шлака в металл---------

турбулентная диффузия, обусловленная тепловой конвекцией и работой перемешивания поднимающихся пузырей и внедряющихся в ванну струй продувочного газа.

С учетом влияния конвекции уравнение диффузии принимает следующий вид:

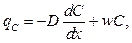(3.60)

где 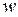– скорость переноса вещества, м/с.

Чаще, в случаях преобладающего влияния турбулентной диффузии, используется эмпирическое уравнение вида

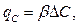(3.61)

где 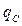– диффузионный поток;

– разность концентраций;

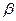– коэффициент массоотдачи (турбулентной диффузии).