Исходные данные задачи №1.5
| Характеристики парка вагонов | Тип вагона | ||||
| Багажный | Почтовый | Плацкартный | Купейный | Мягкий | |
| Число вагонов в поезде, шт.: | |||||
| курьерском | – | ||||
| скором | |||||
| Вместимость вагонов, чел. | – | – | |||
| Наличный парк вагонов, шт. |
Постройте математическую модель задачи, на основании которой можно найти такое соотношение между числом курьерских и скорых поездов, чтобы число ежедневно отправляемых пассажиров достигло максимума.
Задача №1.6*
Управление городским автобусным парком решило провести исследование возможности более рациональной организации своей работы с целью снижения интенсивности внутригородского движения. Сбор и обработка необходимой информации позволили сделать вывод, что необходимое минимальное количество автобусов существенно меняется в течение суток (рис.1.2). Длительность непрерывного использования автобусов на линии равна 8 ч в сутки (с учетом необходимых затрат времени на текущий ремонт и обслуживание). График перекрывающихся смен представлен на рис.1.3.

Рис.1.2. Минимально необходимое количество автобусов на линии
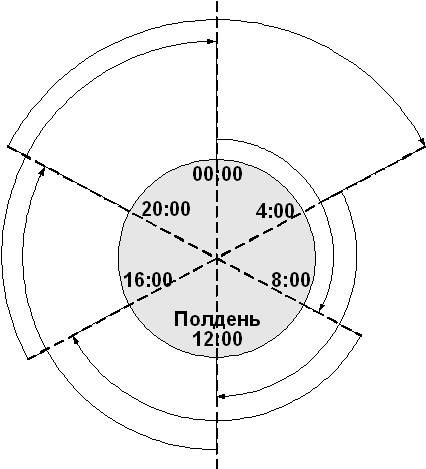
Рис.1.3. График перекрывающихся смен
Постройте математическую модель, позволяющую узнать, какое количество автобусов необходимо выпускать на линию в каждой из смен при условии, что общее количество автобусов, выходящих на линию в течение суток, должно быть минимальным.
Задача №1.7*
Служба снабжения завода получила от поставщиков 500 стальных прутков длиной 5 м. Их необходимо разрезать на детали А и B длиной соответственно 2 и 1,5 м, из которых затем составляются комплекты. В каждый комплект входят 3 детали А и 2 детали B. Характеристики возможных вариантов раскроя прутков представлены в табл.1.5.
Таблица 1.5
Характеристики возможных вариантов раскроя прутков
| Вариант раскроя | Количество деталей, шт./пруток | Отходы, м/пруток | |
| А | B | ||
| 1 | |||
| 2 | |||
| 3 | 0,5 | ||
| Комплектность, шт./компл. |
Постройте математическую модель задачи, позволяющую найти план раскроя прутков, максимизирующий количество комплектов.
Примечание 1.4. В ЦФ могут входить не все переменные задачи.
Задача №1.8*
Малое предприятие выпускает детали А и В. Для этого оно использует литье, подвергаемое токарной обработке, сверлению и шлифованию. Производительность станочного парка предприятия по обработке деталей А и В приведена в табл.1.6.
Предполагая, что спрос на любую комбинацию деталей А и В обеспечен, постройте математическую модель для нахождения плана их выпуска, максимизирующего прибыль.
Таблица 1.6
Исходные данные задачи №1.8
| Станки | Производительность, шт./ч | Стоимость станочного времени, руб./ч | |
| А | В | ||
| Токарные | |||
| Сверлильные | |||
| Шлифовальные | 17,5 | ||
| Цена детали, руб.: | |||
| покупная | |||
| продажная |
Задача №1.9*
Ежедневно в ресторане фирменный коктейль (порция составляет 0,33 л) заказывают в среднем 600 человек. Предполагается, что в ближайшее время их количество увеличится в среднем на 50 человек. Согласно рецепту в составе коктейля должно быть:
· не менее 20%, но и не более 35% спирта;
· не менее 2% сахара;
· не более 5% примесей;
· не более 76% воды;
· не менее 7% и не более 12% сока.
В табл.1.7 приведены процентный состав напитков, из которых смешивается коктейль, и их количество, которое ресторан может ежедневно выделять на приготовление коктейля.
Таблица 1.7
Процентный состав и запасы напитков
| Напиток | Спирт | Вода | Сахар | Примеси | Количество, л/сут. |
| Водка | 40% | 57% | 1% | 2% | |
| Вино | 18% | 67% | 9% | 6% | |
| Сок | 0% | 88% | 8% | 4% |
Постройте модель, на основании которой можно будет определить, хватит ли ресторану имеющихся ежедневных запасов напитков для удовлетворения возросшего спроса на коктейль.
Задача №1.10*
Продукция бумажной фирмы выпускается в виде бумажных рулонов стандартной ширины – по 20 ед. ширины. По специальным заказам потребителей фирма поставляет рулоны и других размеров, для чего производится разрезание стандартных рулонов. Типичные заказы на рулоны нестандартных размеров приведены в табл.1.8.
Таблица 1.8
Варианты заказов на рулоны нестандартных размеров
| Заказ | Требуемая ширина рулона, ед.шир. | Требуемое количество рулонов, шт. |
Все допустимые варианты разрезания рулонов приведены в табл.1.9. Рис.1.4 иллюстрирует 1-й вариант раскроя рулонов.
Таблица 1.9
Допустимые варианты раскроя рулонов
| Требуемая ширина, ед.шир. | Вариант раскроя рулонов | Минимальное кол-во рулонов, шт. | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| Потери, ед.шир. |
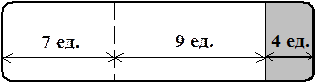
Рис.1.4. 1-й вариант раскроя рулонов
Постройте математическую модель, позволяющую найти такой план разрезания рулонов, при котором поступившие заказы на нестандартные рулоны удовлетворяются с минимальными потерями (т.е. непригодными для реализации остатками рулонов).
Примечание 1.5. В данной задаче для удобства записи модели можно ввести переменные, не являющиеся искомыми величинами.
