Основные методы вычисления пределов

Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:

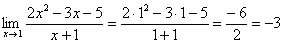
Готово.

Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

Пример с бесконечностью:

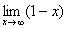
Разбираемся, что такое 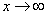? Это тот случай, когда 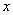неограниченно возрастает, то есть: сначала 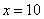, потом 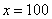, потом , затем и так далее до бесконечности.

А что в это время происходит с функцией ?

, , , …

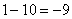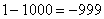Итак: если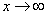 , то функция стремится к минус бесконечности:

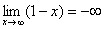
Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию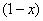 бесконечность и получаем ответ.

Еще один пример с бесконечностью:

Опять начинаем увеличивать 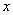до бесконечности, и смотрим на поведение функции:

Вывод: при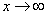 функция 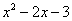неограниченно возрастает

И еще серия примеров:

Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:

, , , , , , , , ,

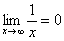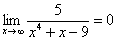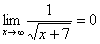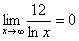
Если где-нибудь есть сомнения, то можете взять в руки калькулятор и немного потренироваться.

В том случае, если 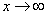, попробуйте построить последовательность 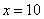, , 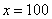. Если , то , , .

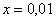Примечание: строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет.

Также обратите внимание на следующую вещь. Даже если дан предел с большим числом вверху, да хоть с миллионом: , то все равно , так как рано или поздно «икс» примет такие гигантские значения, что миллион по сравнению с ними будет самым настоящим микробом.

Что нужно запомнить и понять из вышесказанного?

Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

2) Вы должны понимать и сразу решать простейшие пределы, такие как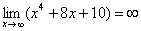 , , и т.д.

Более того, у предела есть очень хороший геометрический смысл. Для лучшего понимания темы рекомендую ознакомиться с методическим материалом Графики и свойства элементарных функций. После прочтения этой статьи вы не только окончательно поймете, что такое предел, но и познакомитесь с очень интересными случаями, когда предела функции вообще не существует!

На практике, к сожалению, подарков немного. А поэтому переходим к рассмотрению более сложных пределов.

6.1.1. Пределы с неопределенностью вида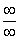 и метод их решения

Сейчас мы рассмотрим группу пределов, когда 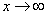, а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены

Пример 1

Вычислить предел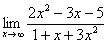

Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида 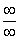. Можно было бы подумать, что 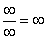, и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.

Как решать пределы данного типа?

Сначала мы смотрим на числитель и находим 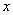в старшей степени:

Старшая степень в числителе равна двум.

Теперь смотрим на знаменатель и тоже находим 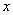в старшей степени:

.

Старшая степень знаменателя равна двум.

Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.

Итак, метод решения следующий: для того, чтобы раскрыть неопределенность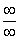 необходимо разделить числитель и знаменатель на 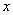в старшей степени.

Разделим числитель и знаменатель на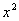

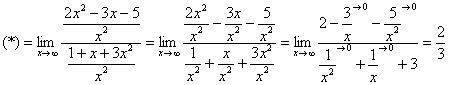
Вот оно как, ответ , а вовсе не бесконечность.