Постановка транспортной задачи
Существуют некоторые специальные классы задач линейного программирования, для решения которых можно использовать специальные методы, позволяющие ускорить процесс решения, учитывая специфику задачи. К таким задачам относятся, например, транспортные задачи (ТЗ).
Рассмотрим общую постановку транспортной задачи.
Постановка задачи. Пусть имеется  пунктов
пунктов  производства некоторого товара, и
производства некоторого товара, и 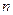 пунктов
пунктов 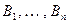 потребления этого товара. Известны запасы товара
потребления этого товара. Известны запасы товара  (
(  ) на каждом пункте производства
) на каждом пункте производства 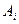 , потребности
, потребности  (
(  ) каждого пункта потребления
) каждого пункта потребления 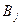 , а также стоимости перевозок товара
, а также стоимости перевозок товара 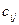 от каждого
от каждого 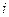 -того пункта производства к каждому
-того пункта производства к каждому 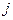 -ому пункту потребления. Требуется составить наиболее экономичный план перевозок товара от пунктов производства к пунктам потребления.
-ому пункту потребления. Требуется составить наиболее экономичный план перевозок товара от пунктов производства к пунктам потребления.
Построим математическую модель задачи.
1). Искомые переменные задачи:
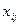 — объем перевозок от
— объем перевозок от 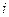 -ого пункта производства к
-ого пункта производства к 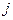 -ому пункту потребления, где
-ому пункту потребления, где  ,
,  .
.
План перевозок можно рассматривать, как вектор  размерности
размерности  .
.
2). Ограничения задачи.
а). Ограничения на возможности вывоза запасов из всех пунктов производства.
Суммарный объем перевозок из каждого пункта производства не может превышать объема, произведенного там товара:
 ,
,  . (2.1)
. (2.1)
b). Ограничения на потребности во всех пунктах потребления.
Суммарные перевозки в каждый пункт потребления должны полностью удовлетворять спрос на товар:
 ,
,  . (2.2)
. (2.2)
с). Ограничения на знак переменных.
Искомые переменные по условию не могут быть отрицательными:
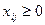 ,
, 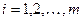 ,
,  . (2.3)
. (2.3)
3). Целевая функция  минимизирует общие затраты на перевозку.
минимизирует общие затраты на перевозку.
Здесь 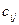 — стоимость перевозок единицы товара от
— стоимость перевозок единицы товара от 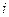 -ого пункта производства к
-ого пункта производства к 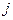 -ому пункту потребления.
-ому пункту потребления.
Математическая постановка транспортной задачи может быть записана в виде:
 (2.4)
(2.4)
 (2.5)
(2.5)
Отметим важное свойство транспортной задачи. Для разрешимости ТЗ необходимо и достаточно, чтобы выполнялось условие баланса, при котором суммарный объем производства равен суммарному объему потребления:
 . (2.6)
. (2.6)
Транспортная задача, для которой выполнено условие баланса (2.6), называется сбалансированной или закрытой. При невыполнении условия (2.6) соответствующая задача называется несбалансированной или открытой.
Заметим, что открытая ТЗ всегда может быть сведена к закрытой путем введения фиктивного пункта производства 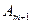 или фиктивного пункта потребления
или фиктивного пункта потребления  .
.
Сбалансированная задача, согласно свойству (2.6) всегда имеет решение.
Рассмотрим сбалансированную задачу. При этом неравенства (2.1) и (2.2) перейдут в равенства. Математическая постановка сбалансированной задачи можно записать в форме ЗЛП:
 (2.7)
(2.7)
 (2.8)
(2.8)
Таким образом, ТЗ является канонической задачей линейного программирования. Ее можно решать с помощью симплекс-метода, описанного в предыдущей главе. Однако на практике для решения ТЗ, в силу ее специфических свойств, можно использовать и другие методы, в частности метод потенциалов.
Решение ТЗ методом потенциалов состоит из двух шагов:
- Нахождение начального допустимого плана.
- Нахождение оптимального решения методом потенциалов.
2.2. Нахождение начального допустимого плана
Начальный допустимый план представляет собой любой план  , удовлетворяющий всем ограничениям исходной задачи. Начальный допустимый план называют также базисным или опорным планом.
, удовлетворяющий всем ограничениям исходной задачи. Начальный допустимый план называют также базисным или опорным планом.
Желательно, найти базисный план, который обеспечит как можно меньшее значение целевой функции. Для этого пользуются специально разработанными методами:
1). Метод северо-западного угла.
2). Метод минимальной стоимости.
3). Метод Фогеля.
Методы отличаются алгоритмом выбора очередной клетки, в которую помещается объем очередной перевозки.
При заполнении транспортной таблицы значениями объемов перевозок 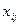 , некоторые клетки могут остаться незаполненными, их называют свободными. Заполненные клетки, соответствующие ненулевым переменным называют занятыми, а сами переменными — базисными.
, некоторые клетки могут остаться незаполненными, их называют свободными. Заполненные клетки, соответствующие ненулевым переменным называют занятыми, а сами переменными — базисными.
Если для сбалансированной задачи число ненулевых переменных 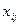 в базисном плане равно
в базисном плане равно 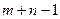 , план называется невырожденным базисным планом.
, план называется невырожденным базисным планом.
План с меньшим, чем 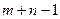 числом ненулевых компонент называется вырожденным планом. В этом случае необходимо ввести в базисный план нулевые переменные и считать их базисными.
числом ненулевых компонент называется вырожденным планом. В этом случае необходимо ввести в базисный план нулевые переменные и считать их базисными.
Исходные данные ТЗ часто задаются в матричном виде:
 | или | 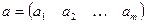 , ,  , , 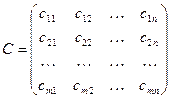 . . |
При решении ТЗ используется транспортная таблица (рис.2.1). Строки таблицы отвечают пунктам производства. В последней клетке каждой строки указан соответствующий объем производства. Например, в первой строке, которая соответствует пункту производства  , объем производства равен
, объем производства равен 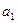 .
.
Столбцы соответствуют пунктам потребления. Последняя клетка каждого столбца содержит объем потребления 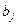 для соответствующего пункта
для соответствующего пункта 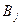 .
.
Каждая клетка транспортной таблицы содержит информацию о перевозке из 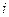 -ого пункта в
-ого пункта в 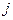 -ый. Здесь
-ый. Здесь 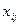 — объем перевозок, а
— объем перевозок, а 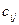 — стоимость перевозки единицы товара.
— стоимость перевозки единицы товара.
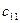  |  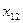 |  | 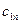 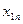 | 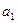 |
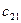 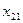 |  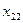 |  | 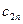 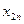 | 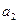 |
 |  | 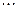 | 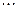 | 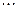 |
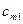 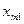 |   |  |  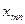 | 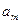 |
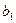 |  |  |  |
Рис. 2.1. Транспортная таблица
Пример 1. Найти начальный допустимый план транспортной задачи, заданной в матричном виде:
 .
.
a). Метод северо-западного угла.
Построим исходную транспортную таблицу.
Первой заполняем клетку в верхнем левом углу  . Присвоим ей значение равное меньшему из объемов спроса
. Присвоим ей значение равное меньшему из объемов спроса  и предложения
и предложения 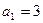 , получим
, получим  . Уменьшим потребности первого пункта потребления и запасы первого пункта производства на 2. Потребности первого пункта потребления исчерпаны, запретим перевозки в этот пункт, используя символ х:
. Уменьшим потребности первого пункта потребления и запасы первого пункта производства на 2. Потребности первого пункта потребления исчерпаны, запретим перевозки в этот пункт, используя символ х:
| Þ |
|
Перейдем к следующей клетке 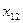 и заполним ее аналогично
и заполним ее аналогично 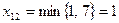 . Уменьшим потребности второго пункта потребления и запасы первого пункта производства на 1. Запасы первого пункта производства при этом будут исчерпаны, запретим перевозки из этого пункта:
. Уменьшим потребности второго пункта потребления и запасы первого пункта производства на 1. Запасы первого пункта производства при этом будут исчерпаны, запретим перевозки из этого пункта:
| Þ |
|
Перейдем к следующей клетке и заполним ее аналогично 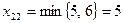 :
:
| Þ |
|
Уменьшим потребности второго пункта потребления и запасы второго пункта производства на 5. Запасы второго пункта производства исчерпаны, запретим перевозки из этого пункта.
Перейдем к следующей клетке, 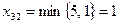 . Уменьшим потребности второго пункта потребления и запасы третьего пункта производства на 1. Потребности второго пункта потребления исчерпаны, запретим перевозки в этот пункт:
. Уменьшим потребности второго пункта потребления и запасы третьего пункта производства на 1. Потребности второго пункта потребления исчерпаны, запретим перевозки в этот пункт:
| Þ |
|
В последнюю клетку запишем 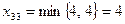 . Уменьшим потребности третьего пункта потребления и запасы третьего пункта производства на 4. Получим допустимый базисный план:
. Уменьшим потребности третьего пункта потребления и запасы третьего пункта производства на 4. Получим допустимый базисный план:
| Þ |
|
Суммы перевозок по строкам и столбцам должны совпадать с исходной задачей. Необходимо выполнить проверку.
Найденный начальный план необходимо также проверить на вырожденность. Вычислим  , количество ненулевых переменных в полученном плане тоже равно 5. Полученный базисный план (рис. 2.2) является невырожденным.
, количество ненулевых переменных в полученном плане тоже равно 5. Полученный базисный план (рис. 2.2) является невырожденным.
| — | ||
| — | — | |
| — |
Рис. 2.2. Начальный базисный план, метод северо-западного угла
Найдем значение целевой функции для найденного плана:
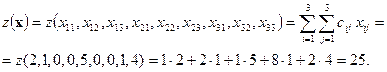
b). Метод минимальной стоимости.
Алгоритм заполнения клеток такой же, как в методе северо-западного угла, изменяется последовательность заполнения клеток. Первой заполняется клетка с минимальной ценой перевозки. Если таких клеток несколько, выбираем любую из них.
Затем выбираем следующую из незаполненных клеток с минимальной ценой, пока не удовлетворим все потребности. При этом все запасы будут использованы полностью, так как рассматривается сбалансированная задача.
Применим метод минимальной стоимости к рассмотренной выше задаче.
Имеются две клетки с минимальной стоимостью перевозки единицы товара  . Заполним сначала клетку
. Заполним сначала клетку  .
.
| Þ |
|
Затем заполним клетку  .
.
| Þ |
|
Следующее по величине значение стоимости равное 2 тоже соответствует двум клеткам  . Заполним сначала клетку
. Заполним сначала клетку 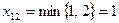 , а затем
, а затем 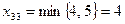 :
:
| Þ |
|
Осталось заполнить клетку  =1 (рис. 2.3). Последовательность заполнения ячеек данным методом:
=1 (рис. 2.3). Последовательность заполнения ячеек данным методом:  ,
, 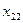 ,
, 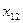 ,
, 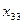 ,
,  .
.
| — | х | ||
| — | — | х | |
| — | х | ||
| х | х | х |
Рис. 2.3. Начальный базисный план, метод минимальной стоимости
Для данной исходной задачи планы, найденные двумя способами, совпали. Заметим, что обычно метод минимальной стоимости дает лучшее начальное решение.
Самым распространённым способом решения транспортной задачи является получение одного из допустимых планов «методом северо-западного угла», который требует меньшего объема вычислений, с последующим его улучшением «методом потенциалов».



 1
1  1
1  1
1  1
1  1
1  5
5