Приложение I. Криволинейные системы координат.
Рис.1.
Прежде всего, нам нужно перейти в уравнении Шредингера (4) к полярным координатам, т.е. нужно в уравнении (4) сделать замену переменных (5). Делается это аналогично одномерному случаю.
Пусть 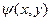 есть решение нашего уравнения. Введем в рассмотрение функцию
есть решение нашего уравнения. Введем в рассмотрение функцию  . Эту функцию определим так, чтобы функция
. Эту функцию определим так, чтобы функция  , совпадала с функцией
, совпадала с функцией  , рассмотренной как сложная функция переменных
, рассмотренной как сложная функция переменных 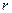 и
и 
 . (7)
. (7)
Эти две функции 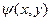 и
и  описывают одно и то же отображение точек комплексной плоскости на множество комплексных чисел – один и тот же закон, который точкам плоскости ставит в соответствие комплексные числа.
описывают одно и то же отображение точек комплексной плоскости на множество комплексных чисел – один и тот же закон, который точкам плоскости ставит в соответствие комплексные числа.
На основании соотношения (6) мы можем написать
 (8)
(8)
и
 (9)
(9)
При дифференцировании функции 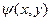 по полярным координатам ее следует рассматривать как сложную функцию
по полярным координатам ее следует рассматривать как сложную функцию 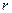 и
и  с
с  и
и 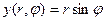 . Согласно правилу дифференцирования сложной функции получаем
. Согласно правилу дифференцирования сложной функции получаем
 (10)
(10)
и
 (11)
(11)
Из (9) и (10), в частности, можно выразить производные по декартовым координатам через производные по полярным. Эти выражения есть
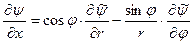 (12)
(12)
и
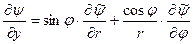 . (13)
. (13)
В частности, из (12) и (13) видно, что для того, чтобы производные 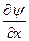 и
и 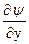 были непрерывны (т.е. чтобы функция
были непрерывны (т.е. чтобы функция 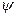 описывала непрерывно дифференцируемое отображение точек плоскости на множество комплексных чисел) нужно, чтобы функция
описывала непрерывно дифференцируемое отображение точек плоскости на множество комплексных чисел) нужно, чтобы функция  также была непрерывно дифференцируемой.
также была непрерывно дифференцируемой.
Вторая производная есть первая производная от первой производной. Таким образом,
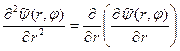 (14)
(14)
и
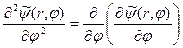 (15)
(15)
Подставляем найденные выражения для первых производных. В результате получаем
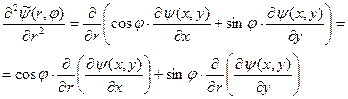 (16)
(16)
и
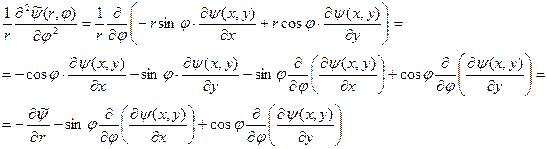 (17)
(17)
При взятии производных по полярными координатам от функций  и
и 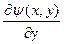 их нужно рассматривать как сложные функции
их нужно рассматривать как сложные функции 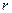 и
и  .
.
Согласно правилу дифференцирования сложной функции имеем
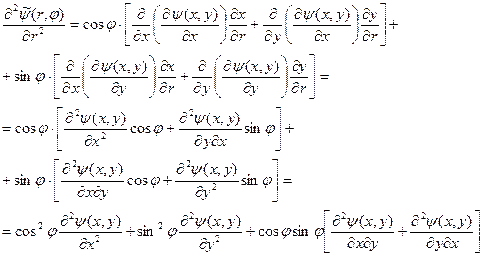 . (18)
. (18)
Аналогично,
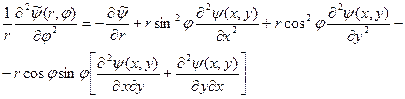 . (19)
. (19)
Итак, имеем
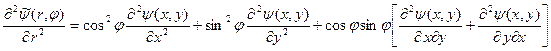 (20)
(20)
и
 . (21)
. (21)
Сложив (20) и (21), находим нужную нам сумму вторых производных (лапласиан двумерной функции)
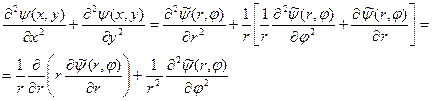 . (22)
. (22)
Таким образом, стационарное уравнение Шредингера нашей частицы в полярных координатах имеет вид
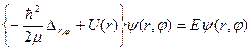 , (23)
, (23)
где
 . (24)
. (24)
К тому же самому результату мы можем прийти с помощью более простых рассуждений, основанных на материале, изложенном в приложении I.
Обратим внимание на правую часть уравнения (23). Там присутствует оператор 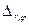 . Этот оператор преобразует функции переменных
. Этот оператор преобразует функции переменных 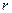 и
и  .
.
Пусть 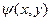 есть некоторая функция декартовых координат точек на плоскости. Она описывает закон, который каждой точке плоскости ставит в соответствие комплексное число. Такой закон называется отображением точек плоскости на множество комплексных чисел.
есть некоторая функция декартовых координат точек на плоскости. Она описывает закон, который каждой точке плоскости ставит в соответствие комплексное число. Такой закон называется отображением точек плоскости на множество комплексных чисел.
Поскольку точку на плоскости мы можем однозначным образом задать полярными координатами, то тоже самое отображение мы можем описать с помощью функции  полярных координат. Эта функция
полярных координат. Эта функция  , очевидно, представляет собой функцию
, очевидно, представляет собой функцию 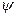 , рассмотренную как сложную функцию
, рассмотренную как сложную функцию 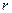 и
и  .
.
 , (25)
, (25)
где  и
и 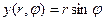 .
.
В результате действия оператора Лапласа 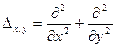 на функцию
на функцию 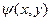 мы опять получаем функцию
мы опять получаем функцию 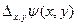 декартовых координат, которая также описывает некоторое отображение точек комплексной плоскости на множество комплексных чисел.
декартовых координат, которая также описывает некоторое отображение точек комплексной плоскости на множество комплексных чисел.
Из проведенных выше выкладок видно, что функция полярных координат  описывает то же самое отображение, что и функция
описывает то же самое отображение, что и функция  .
.
Итак, если функции 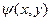 и
и  описывают одно и то же отображение, то и функции
описывают одно и то же отображение, то и функции 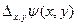 и
и  также описывают одно и то же отображение. Другими словами,
также описывают одно и то же отображение. Другими словами, 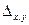 и
и 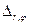 устанавливают один и тот же закон, связывающий между собой различные отображения. Поэтому если под оператором в общем смысле понимать закон, связывающий между собой отображения, то можно сказать, что
устанавливают один и тот же закон, связывающий между собой различные отображения. Поэтому если под оператором в общем смысле понимать закон, связывающий между собой отображения, то можно сказать, что 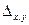 и
и 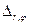 представляют собой один и тот же оператор (двумерный оператор Лапласа), заданный в различных системах координат – декартовой и полярной соответственно.
представляют собой один и тот же оператор (двумерный оператор Лапласа), заданный в различных системах координат – декартовой и полярной соответственно.
Соответственно, правая часть уравнения Шредингера (23) есть ни что иное как оператор Гамильтона, заданный в полярных координатах
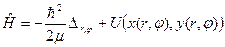 . (26)
. (26)
Найти оператор Лапласа мы можем ,не проделывая проведенных выше выкладок, а воспользовавшись теорией криволинейных координат, элементы которой изложены в приложении I. Только теперь у нас пространство двумерное. Соответственно, базис состоит из двух векторов.
В соответствие с (ПI.8) и (5) коэффициенты Ламэ, отвечающие полярным координатам 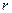 и
и  есть
есть
 (27)
(27)
и
 (28)
(28)
В соответствие с (ПI.7) орты полярной системы координат есть
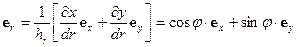 (29)
(29)
и
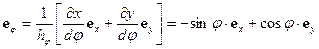 . (30)
. (30)
Легко видеть, что в каждой точке пространства
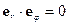 . (31)
. (31)
Таким образом, в каждой точке орты  и
и 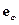 полярной системы координат являются попарно ортогональными. Следовательно, полярная система координат является ортогональной. Также несложно убедиться, что
полярной системы координат являются попарно ортогональными. Следовательно, полярная система координат является ортогональной. Также несложно убедиться, что  и
и 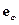 образуют правую пару векторов.
образуют правую пару векторов.
В соответствие с (ПI.12) оператор Лапласа в полярной системе координат
 . (32)
. (32)
Итак, при переходе в уравнении Шредингера от декартовых координат 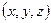 к криволинейным
к криволинейным  можно поступать следующим образом. Прежде всего, записываем оператор Гамильтона в координатах
можно поступать следующим образом. Прежде всего, записываем оператор Гамильтона в координатах  . Для этого нужно, используя математический аппарат, изложенный в приложении I, найти оператор Лапласа
. Для этого нужно, используя математический аппарат, изложенный в приложении I, найти оператор Лапласа 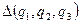 в рассматриваемой криволинейной системе координат, а также, воспользовавшись выражениями декартовых координат через криволинейные, нужно потенциал
в рассматриваемой криволинейной системе координат, а также, воспользовавшись выражениями декартовых координат через криволинейные, нужно потенциал 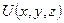 представить как функцию криволинейных координат
представить как функцию криволинейных координат  . Т.е. если оператор Гамильтона частицы в декартовых координатах имеет вид
. Т.е. если оператор Гамильтона частицы в декартовых координатах имеет вид
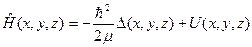 , (33)
, (33)
где 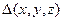 - оператор Лапласа в декартовых координатах, то гамильтониан в криволинейных координатах
- оператор Лапласа в декартовых координатах, то гамильтониан в криволинейных координатах 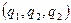 дается выражением
дается выражением
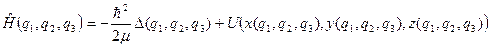 . (34)
. (34)
Здесь 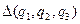 - оператор Лапласа, заданный в криволинейной системе координат
- оператор Лапласа, заданный в криволинейной системе координат  . Он определяется с помощью математического аппарата, изложенного в приложении I. Соответственно, стационарное уравнение Шредингера в криволинейных координатах имеет вид
. Он определяется с помощью математического аппарата, изложенного в приложении I. Соответственно, стационарное уравнение Шредингера в криволинейных координатах имеет вид
 . (35)
. (35)
Однако, при переходе от декартовых координат к криволинейным нужно быть очень аккуратным с требованием однозначности. Дело здесь в следующем.
Пусть мы решаем дифференциальное уравнение
 (36)
(36)
при дополнительном требовании однозначности решения во всем пространстве. Здесь  - это некий дифференциальный оператор, преобразующий функции декартовых коордиат. Например, в нашем случае
- это некий дифференциальный оператор, преобразующий функции декартовых коордиат. Например, в нашем случае  представляет собой оператор Гамильтона частицы (2).
представляет собой оператор Гамильтона частицы (2).
Рассмотрим некоторую криволинейную систему координат 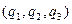 . Переходя в уравнении (36) от декартовых координат к криволинейным, мы получаем эквивалентное ему уравнение
. Переходя в уравнении (36) от декартовых координат к криволинейным, мы получаем эквивалентное ему уравнение
 (37)
(37)
Здесь  есть оператор
есть оператор  , заданный в криволинейных координатах
, заданный в криволинейных координатах  . Например, в рассматриваемом нами случае оператор
. Например, в рассматриваемом нами случае оператор  представляет собой оператор Гамильтона (26).
представляет собой оператор Гамильтона (26).
Эквивалентность уравнений (36) и (37) означает следующее. Возьмем произвольную функцию  переменных
переменных 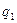 ,
, 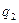 и
и 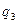 . Эта функция описывает некоторое отображение реального пространства на множество комплексных чисел, т.е. она описывает некоторый закон, который точкам пространства ставит в соответствие комплексные числа. Этот же закон, очевидно, можно описать также и с помощью некоторой функции
. Эта функция описывает некоторое отображение реального пространства на множество комплексных чисел, т.е. она описывает некоторый закон, который точкам пространства ставит в соответствие комплексные числа. Этот же закон, очевидно, можно описать также и с помощью некоторой функции  декартовых координат. Функция
декартовых координат. Функция 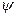 , очевидно, будет получаться из функции
, очевидно, будет получаться из функции  , если мы в функцию
, если мы в функцию  подставим выражения для криволинейных координат через декартовы. Естественно, справедливо, и обратное. Если мы в функцию
подставим выражения для криволинейных координат через декартовы. Естественно, справедливо, и обратное. Если мы в функцию 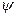 подставим выражение для декартовых координат через криволинейные, то мы получим функцию
подставим выражение для декартовых координат через криволинейные, то мы получим функцию  .
.
Эквивалентность уравнений (36) и (37) означает, что если функция  есть решение уравнения (37), то решением уравнения (36) будет является функция
есть решение уравнения (37), то решением уравнения (36) будет является функция  , которая описывает то же самое отображение, что и функция
, которая описывает то же самое отображение, что и функция  . Соответственно и наоборот. если функция
. Соответственно и наоборот. если функция  есть решение уравнения (36), то решением уравнения (37) будет является функция
есть решение уравнения (36), то решением уравнения (37) будет является функция  , которая описывает то же самое отображение, что и функция
, которая описывает то же самое отображение, что и функция  .
.
Нас интересуют только однозначные во всем пространстве решения уравнения (36). Эти решения описывают однозначные отображения реального пространства на множество комплексных чисел, т.е. такие отображения, которые данной точке пространства ставят в соответствие единственное комплексное число.
Поэтому нас должны интересовать только те решения уравнения (37), которые описывают однозначные отображения. Только такие решения после подстановки в них выражений для криволинейных координат через декартовы дадут нам однозначные решения уравнения (36). Все же остальные решения уравнения (37) не будут нам давать однозначных решений уравнения (36).
Осторожность нужно проявлять в следующем. В число криволинейных координат могут входить циклические координаты. Пусть в рассматриваемой криволинейной координатной системе координата 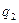 является циклической. Это означает, что существует ее приращение
является циклической. Это означает, что существует ее приращение 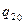 такое, что криволинейные координаты
такое, что криволинейные координаты  и криволинейные координаты
и криволинейные координаты 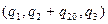 отвечают одной и той же точке пространства. В таком случае мы на решения уравнения (37) должны наложить дополнительное условие
отвечают одной и той же точке пространства. В таком случае мы на решения уравнения (37) должны наложить дополнительное условие
 . (38)
. (38)
Это условие обусловлено требованием однозначности решения исходного уравнения (36). Если решение уравнения (37) этому условию не удовлетворяет, то это решение не будет описывать однозначное отображение реального пространства на множество комплексных чисел. Следовательно, после подстановки в него выражений криволинейных координат через декартовы мы заведомо не получим однозначное решение уравнения (36).
В полярной системе координат (в данном случае реальное пространство двумерное, и, соответственно, криволинейный координат у нас две) циклической координатой является полярный угол  . Полярные координаты
. Полярные координаты 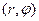 и сферические координаты
и сферические координаты  отвечают одной и той же точке пространства. Поэтому, когда стационарное уравнение Шредингера (4) мы решаем в сферических координатах, мы должны на решения этого уравнения налагать дополнительное требование
отвечают одной и той же точке пространства. Поэтому, когда стационарное уравнение Шредингера (4) мы решаем в сферических координатах, мы должны на решения этого уравнения налагать дополнительное требование
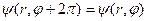 . (39)
. (39)
Таким образом, стационарное уравнение Шредингера (4) имеет однозначные конечные непрерывно дифференцируемые во всем пространстве нетривиальные решения тогда и только тогда, когда эквивалентное ему уравнение (23) в полярных сферических координатах имеет решения, которые являются однозначными конечными непрерывно дифференцируемыми функциями 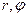 и, кроме того, еще и удовлетворяют условию (39). Если уравнение в полярных координатах даже и имеет однозначные конечные непрерывно дифференцируемые при всех
и, кроме того, еще и удовлетворяют условию (39). Если уравнение в полярных координатах даже и имеет однозначные конечные непрерывно дифференцируемые при всех 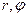 решения, но ни одно из этих решений не удовлетворяет указанному условию (39), то исходное уравнение (4) однозначных решений не имеет. А, следовательно, соответствующее значение
решения, но ни одно из этих решений не удовлетворяет указанному условию (39), то исходное уравнение (4) однозначных решений не имеет. А, следовательно, соответствующее значение  энергии является недопустимым.
энергии является недопустимым.
Итак, данное значение  энергии нашей частицы является допустимым тогда и только тогда, когда уравнение Шредингера в полярных координатах
энергии нашей частицы является допустимым тогда и только тогда, когда уравнение Шредингера в полярных координатах
 . (40)
. (40)
имеет однозначные конечные непрерывно дифференцируемые нетривиальные решения, удовлетворяющие условию (39). Сами эти решения являются волновыми функциями стационарных состояний с данным значением энергии  .
.
Оператор в правой части уравнения (40) – оператор Гамильтона нашей частицы в полярной системе координат- состоит из двух частей. Первая часть  представляет собой линейный оператор, который содержит только радиальную координату и производные по ней. Полярной координаты в этой части оператора нет. Если мы возьмем произведение двух функций, одна из которых зависит только от радиальной координаты и не зависит от угла
представляет собой линейный оператор, который содержит только радиальную координату и производные по ней. Полярной координаты в этой части оператора нет. Если мы возьмем произведение двух функций, одна из которых зависит только от радиальной координаты и не зависит от угла  , а другая наоборот зависит только от полярной координаты и не зависит от радиальной переменной
, а другая наоборот зависит только от полярной координаты и не зависит от радиальной переменной 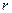 ,и подействуем на эту функцию первой частью оператора Гамильтона, то зависящую только от
,и подействуем на эту функцию первой частью оператора Гамильтона, то зависящую только от  функцию мы можем вынести из под знака этого оператора
функцию мы можем вынести из под знака этого оператора
 . (41)
. (41)
Вторая часть  оператора Гамильтона есть произведение функции, которая зависит только от радиальной координаты
оператора Гамильтона есть произведение функции, которая зависит только от радиальной координаты 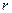 и не зависит от угла
и не зависит от угла  , на линейный оператор, который не содержит радиальную переменную
, на линейный оператор, который не содержит радиальную переменную 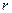 . Если мы подействуем этой второй частью на произведение функций, одна из которых зависит только от радиальной координаты, а другая только от полярного угла, то функцию, зависящую только от радиальной координаты, мы можем вынести за знак этого оператора
. Если мы подействуем этой второй частью на произведение функций, одна из которых зависит только от радиальной координаты, а другая только от полярного угла, то функцию, зависящую только от радиальной координаты, мы можем вынести за знак этого оператора
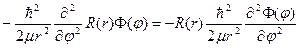 . (42)
. (42)
Как мы уже знаем, в таком уравнении можно провести так называемую процедуру разделения переменных. Ищем решение нашего уравнения в виде
 . (43)
. (43)
Подставляем это решение в наше стационарное уравнение и пользуемся соотношениями (42) и (43).
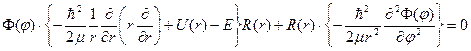 . (44)
. (44)
Делим обе части уравнения на произведение функций R и 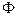 . Умножаем обе части на
. Умножаем обе части на 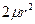 .
.
 . (45)
. (45)
Смотрим внимательно на правую часть получившегося уравнения. Первое слагаемое в правой части представляет собой функцию, которая зависит только от радиальной координаты 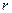 и не зависит от полярного угла
и не зависит от полярного угла  . Вторая часть напротив представляет собой функцию, которая зависит только от
. Вторая часть напротив представляет собой функцию, которая зависит только от  и не зависит от радиальной переменной. Причем сумма этих функций тождественно, т.е. во всех точках, равна нулю. Такое возможно только тогда, когда обе этих функции есть противоположные по знаку константы. Давайте константу, которой равна вторая функция обозначим
и не зависит от радиальной переменной. Причем сумма этих функций тождественно, т.е. во всех точках, равна нулю. Такое возможно только тогда, когда обе этих функции есть противоположные по знаку константы. Давайте константу, которой равна вторая функция обозначим 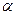 . Тогда первая функция будет равна этой константе, взятой со знаком минус.
. Тогда первая функция будет равна этой константе, взятой со знаком минус.
Таким образом, функция  является удовлетворяющим стандартным требованиям к волновой функции тогда и только тогда, когда функция
является удовлетворяющим стандартным требованиям к волновой функции тогда и только тогда, когда функция 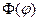 является однозначным конечным непрерывно дифференцируемым нетривиальным решением уравнения
является однозначным конечным непрерывно дифференцируемым нетривиальным решением уравнения
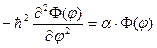 , (46)
, (46)
удовлетворяющим условию (вытекает из (39))
 , (47)
, (47)
а функция R является однозначным конечным непрерывно дифференцируемым нетривиальным решением уравнения
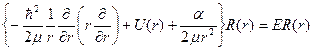 . (48)
. (48)
Более того, соответствующая теорема математической физики утверждает, что из таких решений мы можем сформировать полный и ортонормированный функциональный набор  . По этой базисной системе мы можем разложить любую функцию, удовлетворяющую стандартным требованиям. В частности, общее решение уравнения Шредингера с данным значением энергии имеет вид
. По этой базисной системе мы можем разложить любую функцию, удовлетворяющую стандартным требованиям. В частности, общее решение уравнения Шредингера с данным значением энергии имеет вид
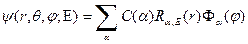 . (49)
. (49)
Решением уравнений (46) и (48) мы займемся в следующей части данного материала.
Приложение I. Криволинейные системы координат.
Введем в пространстве декартову систему координат. Точку в пространстве можно однозначным образом задать, указав три ее декартовы координаты x, y и z. Радиус-вектор точки представляет собой вектор, исходящий из начала координат, и заканчивающийся в этой точке Радиус-вектор точки пространства выражается через декартовы координаты как
 . (ПI.1)
. (ПI.1)
Здесь  ,
,  и
и  - орты декартовой системы координат.
- орты декартовой системы координат.
Однако использование декартовых координат далеко не всегда бывает удобным. В некоторых случаях гораздо удобнее пользоваться криволинейными координатами.
Любые три независимые переменные, однозначно задающие положение точки в пространстве, могут быть выбраны в качестве координат этой точки. Такие координаты называются криволинейными  ,
, 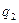 ,
, 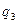 . Декартовы координаты можно рассматривать как частный случай криволинейных координат.
. Декартовы координаты можно рассматривать как частный случай криволинейных координат.
Радиус вектор точки 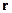 будет векторной функцией криволинейных координат
будет векторной функцией криволинейных координат
 . (2)
. (2)
Соответственно, декартовы координаты будут выражаться через криволинейные координаты с помощью соотношений
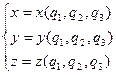 . (3)
. (3)
Например, положение точки пространства можно задавать в сферической системе координат. В сферической системе координат точка пространства задается длинной ее радиус-вектора, т.е. расстоянием от точки до начала координат (радиальная координата), указанием угла 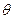 , который радиус-вектор образует с осью z (азимутальный угол или азимутальная координата), и указанием угла
, который радиус-вектор образует с осью z (азимутальный угол или азимутальная координата), и указанием угла  , который образует с осью х проекция радиус вектора на плоскость х,y (полярный угол или полярная координата). Указав
, который образует с осью х проекция радиус вектора на плоскость х,y (полярный угол или полярная координата). Указав 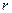 ,
, 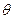 и
и  , мы однозначным образом задаем точку в пространстве (рис.1). Таким образом, в случае сферической системы координат
, мы однозначным образом задаем точку в пространстве (рис.1). Таким образом, в случае сферической системы координат  ,
, 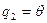 и
и 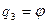 .
.
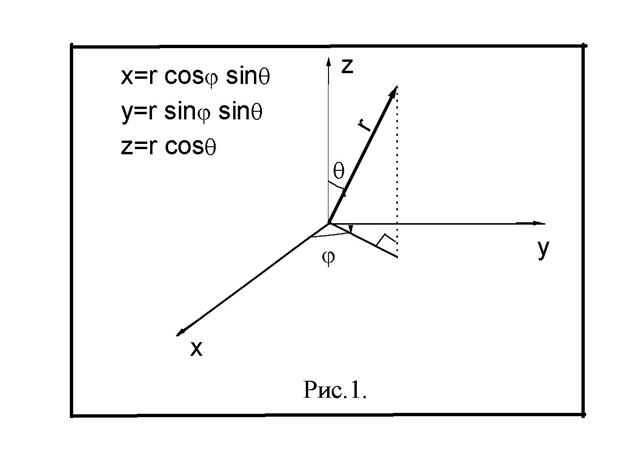
Декартовы координаты выражаются через сферические с помощью соотношений
 . (ПI.4)
. (ПI.4)
Соответственно, радиус вектор как векторная функция сферических координат имеет вид
 . (ПI.5)
. (ПI.5)
Рассмотрим общие геометрические свойства, характерные для всех систем криволинейных координат.
Координатными линями, отвечающими данной координате, называются непрерывные кривые, вдоль которых меняется только эта координата, а все остальные координаты рассматриваемой системы остаются постоянными. Для того, чтобы провести через точку  координатную линию, отвечающую координате
координатную линию, отвечающую координате 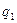 , нужно зафиксировать значения двух координат
, нужно зафиксировать значения двух координат 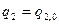 и
и  и непрерывно изменять координату
и непрерывно изменять координату 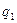 , тогда конец радиус вектора
, тогда конец радиус вектора 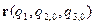 будет описывать в пространстве требуемую координатную линию. Договоримся проходящую через точку
будет описывать в пространстве требуемую координатную линию. Договоримся проходящую через точку  координатную линию, отвечающую координате
координатную линию, отвечающую координате 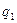 , обозначать
, обозначать 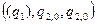 . Аналогично, если мы зафиксируем значения координат
. Аналогично, если мы зафиксируем значения координат  и
и 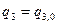 и будем непрерывно изменять координату
и будем непрерывно изменять координату 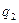 , то конец радиус-вектора
, то конец радиус-вектора  будет описывать проходящую через точку
будет описывать проходящую через точку  координатную линию, отвечающую координате
координатную линию, отвечающую координате 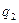 . Эту координатную линию будем обозначать
. Эту координатную линию будем обозначать  . Точно также для того, чтобы провести через точку
. Точно также для того, чтобы провести через точку  координатную линию, отвечающую координате
координатную линию, отвечающую координате 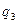 , нужно зафиксировать значения двух координат
, нужно зафиксировать значения двух координат  и
и 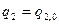 и непрерывно изменять координату
и непрерывно изменять координату 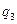 , тогда конец радиус вектора
, тогда конец радиус вектора  будет описывать в пространстве требуемую координатную линию. Эту координатную линию, соответственно, обозначаем
будет описывать в пространстве требуемую координатную линию. Эту координатную линию, соответственно, обозначаем  .
.
Введем теперь понятие ортов (локального базиса) криволинейной системы координат. В орты декартовой системы координат 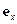 ,
,  и
и  являются фиксированными векторами – они одинаковы во всех точках пространтсва. Векторная функция
являются фиксированными векторами – они одинаковы во всех точках пространтсва. Векторная функция 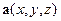 выражается через орты
выражается через орты 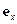 ,
,  и
и  как
как
 . (ПI.6)
. (ПI.6)
Здесь  - проекция вектора
- проекция вектора 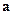 на направление орта
на направление орта 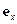 (на декартову ось х),
(на декартову ось х),  - проекция вектора
- проекция вектора 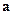 на направление орта
на направление орта  (на декартову ось у),
(на декартову ось у), 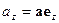 - проекция вектора
- проекция вектора 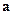 на направление орта
на направление орта  (на декартову ось z).
(на декартову ось z).
. В криволинейной же системе координат орты, вообще говоря, зависят от точки. В общем случае орты в различных точках пространства разные. В каждой точке пространства определены три орта криволинейной системы координат. Обозначим 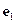 - орт, отвечающий координате
- орт, отвечающий координате 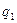 . Обозначим
. Обозначим 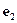 - орт, отвечающий координате
- орт, отвечающий координате 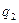 . Обозначим
. Обозначим  - орт, отвечающий координате
- орт, отвечающий координате 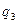 .
.
Для того, чтобы найти орты 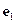 ,
, 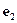 и
и  в точке
в точке  , нужно через эту точку провести три координатные линии -
, нужно через эту точку провести три координатные линии - 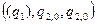 ,
,  и
и  . Орт
. Орт 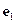 в точке
в точке 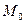 представляет собой единичных вектор, параллельный касательной к координатной линии
представляет собой единичных вектор, параллельный касательной к координатной линии 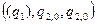 в этой точке. Направлен он в сторону возрастания координаты
в этой точке. Направлен он в сторону возрастания координаты 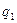 . (в сторону, в которую движется конец радиус вектора
. (в сторону, в которую движется конец радиус вектора 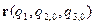 из точки
из точки 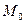 при увеличении координаты
при увеличении координаты 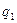 ). Единичный вектор, направленный по касательной к координатной линии
). Единичный вектор, направленный по касательной к координатной линии  в точке
в точке 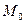 в сторону увеличения координаты
в сторону увеличения координаты 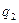 , является ортом
, является ортом 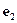 . Единичный вектор, направленный по касательной к координатной линии
. Единичный вектор, направленный по касательной к координатной линии  в точке
в точке 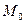 в сторону увеличения координаты
в сторону увеличения координаты 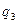 , представляет собой орт
, представляет собой орт  . Другими словами, для того, чтобы найти в данной точке орт, отвечающий данной координате, нужно через эту точку провести координатную линию, отвечающую данной координате. Затем нужно найти касательную к этой кривой в рассматриваемой точке. Искомый орт представляет собой единичный вектор, направленный вдоль этой касательной в сторону увеличения данной координаты.
. Другими словами, для того, чтобы найти в данной точке орт, отвечающий данной координате, нужно через эту точку провести координатную линию, отвечающую данной координате. Затем нужно найти касательную к этой кривой в рассматриваемой точке. Искомый орт представляет собой единичный вектор, направленный вдоль этой касательной в сторону увеличения данной координаты.
Орты 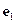 ,
, 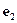 и
и  криволинейной системы координат выражаются через производные векторной функции
криволинейной системы координат выражаются через производные векторной функции  , взятые по соответствующим координатам, следующим образом
, взятые по соответствующим координатам, следующим образом
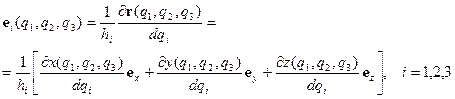 . (ПI.7)
. (ПI.7)
Здесь
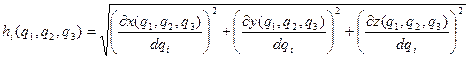 . (ПI.8)
. (ПI.8)
Функции обобщенных координат 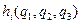 называются коэффициентами Ламе.
называются коэффициентами Ламе.
В общем случае орты 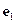 ,
, 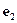 и
и  вовсе не обязательно являются ортогональными, т.е. вовсе не обязательно в каждой точке скалярное произведение
вовсе не обязательно являются ортогональными, т.е. вовсе не обязательно в каждой точке скалярное произведение 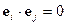 при
при  .
.
В том случае, когда в каждой точке орты 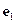 ,
, 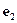 и
и  криволинейной системы координат являются попарно ортогональными, т.е. когда в каждой точке
криволинейной системы координат являются попарно ортогональными, т.е. когда в каждой точке 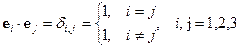 , то эта криволинейная система координат называется ортогональной.
, то эта криволинейная система координат называется ортогональной.
Договоримся в дальнейшем считать по умолчанию рассматриваемую координатную систему ортогональной.
Также в дальнейшем будем полагать, что орты 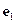 ,
, 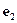 и
и  образуют правую тройку векторов, т.е. что криволинейная система координат является правой.
образуют правую тройку векторов, т.е. что криволинейная система координат является правой.
Любой вектор 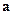 в любой точке пространства можно разложить по соответствующим ортам
в любой точке пространства можно разложить по соответствующим ортам 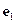 ,
, 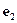 и
и  криволинейной системы координат, т.е. можно представить в виде
криволинейной системы координат, т.е. можно представить в виде
 . (ПI.9)
. (ПI.9)
В соответствие с (ПI.7) компоненты 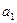 ,
,  и
и 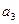 вектора
вектора 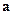 в криволинейной системе координат (его проекции на орты
в криволинейной системе координат (его проекции на орты 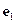 ,
, 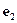 и
и  ) выражаются через компоненты
) выражаются через компоненты  этого вектора в декартовой системе координат следующим образом
этого вектора в декартовой системе координат следующим образом
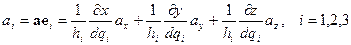 . (ПI.10)
. (ПI.10)
Градиент функции 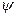 точки пространства (описывает отображение точек пространства на множество комплексных чисел – закон, ставящий в соответствие точкам пространства комплексные числа), заданной в криволинейных координатах
точки пространства (описывает отображение точек пространства на множество комплексных чисел – закон, ставящий в соответствие точкам пространства комплексные числа), заданной в криволинейных координатах 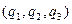 определяется выражением
определяется выражением
 . (ПI.11)
. (ПI.11)
Лапласинан функции 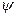 точки пространства, заданной в криволинейных координатах
точки пространства, заданной в криволинейных координатах 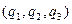 определяется выражением
определяется выражением
 . (ПI.12)
. (ПI.12)
Дивергенция векторной функции 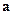 точки в пространстве (описывает отображение точек пространства на множество комплексных геометрических векторов – закон, ставящий в соответствие точкам пространства комплексные геометрические векторы), заданной в криволинейных координатах
точки в пространстве (описывает отображение точек пространства на множество комплексных геометрических векторов – закон, ставящий в соответствие точкам пространства комплексные геометрические векторы), заданной в криволинейных координатах 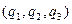 определяется выражением
определяется выражением
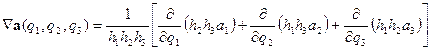 . (ПI.13)
. (ПI.13)
Ротор векторной функции 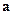 точки в пространстве, заданной в криволинейных координатах
точки в пространстве, заданной в криволинейных координатах 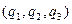 определяется выражением
определяется выражением
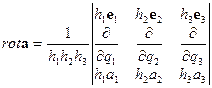 . (ПI.14)
. (ПI.14)
В качестве примера рассмотрим сферическую систему координат. В этом случае  ,
, 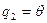 и
и 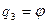 . Связь декартовых координат со сферическими дается (ПI.4). Для наглядности орт радиальной координаты
. Связь декартовых координат со сферическими дается (ПI.4). Для наглядности орт радиальной координаты 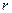 обозначим
обозначим  , орт азимутальной координаты
, орт азимутальной координаты 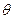 -
-  , и орт полярной координаты
, и орт полярной координаты  обозначим
обозначим 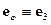 . Соответственно, коэффициент Ламе радиальной координаты
. Соответственно, коэффициент Ламе радиальной координаты 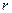 обозначим
обозначим 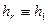 , коэффициент Ламе азимутальной координаты
, коэффициент Ламе азимутальной координаты 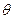 -
- 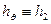 , коэффициент Ламе полярной координаты
, коэффициент Ламе полярной координаты  обозначим
обозначим  . Компоненты вектора
. Компоненты вектора 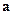 в базисе сферической системы координат будем обозначать
в базисе сферической системы координат будем обозначать  ,
, 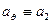 и
и  .
.
Производные декартовых координат по радиальной координате 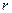 есть
есть
 , (ПI.15)
, (ПI.15)
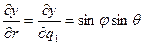 , (ПI.16)
, (ПI.16)
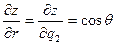 . (ПI.17)
. (ПI.17)
Соответственно, коэффициент Ламе, отвечающий радиальной координате, есть
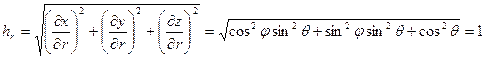 . (ПI.18)
. (ПI.18)
Производные декартовых координат по азимутальной координате 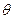 есть
есть
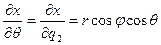 , (ПI.19)
, (ПI.19)
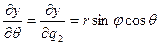 , (ПI.20)
, (ПI.20)
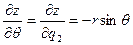 . (ПI.21)
. (ПI.21)
Соответственно, коэффициент Ламе, отвечающий азимутальной координате, есть
 . (ПI.22)
. (ПI.22)
Производные декартовых координат по полярной координате 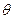 есть
есть
 , (ПI.23)
, (ПI.23)
 , (ПI.24)
, (ПI.24)
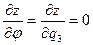 . (ПI.25)
. (ПI.25)
Соответственно, коэффициент Ламе, отвечающий полярной координате, есть
 . (ПI.26)
. (ПI.26)
В последнем выражении учтено, что азимутальная координата 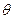 меняется в пределах отрезка
меняется в пределах отрезка 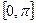 . Поэтому
. Поэтому 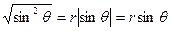 .
.
В соответствие с (ПI.7) орты  ,
,  и
и 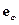 выражается через орты
выражается через орты 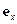 ,
,  и
и  декартовой системы координат как
декартовой системы координат как
 , (ПI.27)
, (ПI.27)
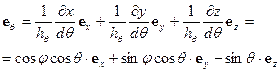 , (ПI.28)
, (ПI.28)
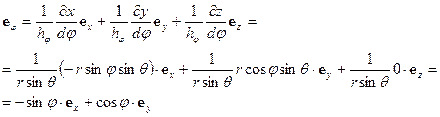 . (ПI.29)
. (ПI.29)
Несложно напрямую убедиться, что в каждой точке пространства
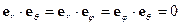 . (ПI.30)
. (ПI.30)
Таким образом, в каждой точке орты  ,
,  и
и 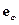 сферической системы координат являются попарно ортогональными (образуют ортогональную тройку векторов). Следовательно, сферическая система координат является ортогональной. Также несложно убедиться, что
сферической системы координат являются попарно ортогональными (образуют ортогональную тройку векторов). Следовательно, сферическая система координат является ортогональной. Также несложно убедиться, что  ,
,  и
и 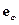 образуют правую тройку векторов.
образуют правую тройку векторов.
Выразим компоненты вектора 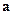 в сферической системе координат через его компоненты в декартовой координатной системе.
в сферической системе координат через его компоненты в декартовой координатной системе.
 , (ПI.31)
, (ПI.31)
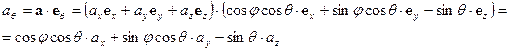 , (ПI.32)
, (ПI.32)
 . (ПI.33)
. (ПI.33)
В соответствие с (ПI.11) градиент функции 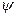 точки пространства, заданной в сферических координатах
точки пространства, заданной в сферических координатах 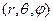 определяется выражением
определяется выражением
 . (ПI.34)
. (ПI.34)
В соответствие с (ПI.12) лапласиан функции 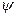 точки пространства, заданной в сферических координатах
точки пространства, заданной в сферических координатах 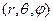 определяется выражением
определяется выражением
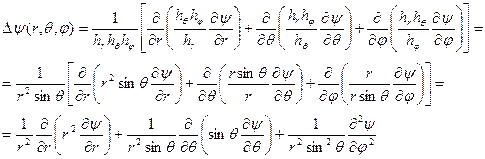 . (ПI.35)
. (ПI.35)
В соответствие с (ПI.13) дивергенция векторной функции 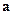 точки в пространстве заданной в сферических координатах
точки в пространстве заданной в сферических координатах 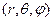 определяется выражением
определяется выражением
 . (ПI.36)
. (ПI.36)
Ротор векторной функции 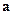 точки в пространстве, заданной в в сферических координатах
точки в пространстве, заданной в в сферических координатах 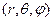 определяется выражением
определяется выражением
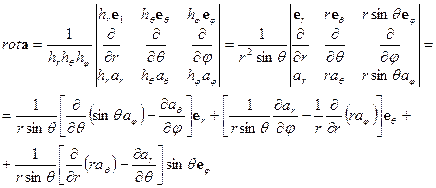 . (ПI.37)
. (ПI.37)
