Адание к расчетно-графической работе 2
адание к расчетно-графической работе 1
Используя метод штрафных функций, решить задачи нелинейного программирования: найти максимальное и минимальное значения функции z=f(x1,x2) при заданных ограничениях на ее переменные. Условия задачи приведены в приложении А.
Порядок выполнения работы
1 Построить вручную область допустимых решений, определяемую ограничениями задачи нелинейного программирования.
2 Определить тип поверхности, описываемой целевой функцией, и тип ее линий уровня.
3 Составить штрафную и вспомогательную целевую функции для решения задачи нелинейного программирования методом штрафных функций.
4 Определить исходную допустимую точку, из которой будет начато движение к экстремуму.
5 Выбрать метод оптимизации вспомогательной целевой функции.
6 Составить программу для оптимизации вспомогательной целевой функции выбранным методом безусловной оптимизации. Предусмотреть в программе графическую интерпретацию поиска экстремумов с построением области допустимых решений и линий уровня целевой функции.
7 Выполнить поиск глобального минимума.
8 Выполнить поиск глобального максимума. Учесть тип поверхности отклика.
9 Оформить отчет о работе.
Содержание отчета
Отчет должен содержать:
1 Постановку задачи нелинейного программирования.
2 Исследование целевой функции на выпуклость и вогнутость и полученный тип поверхности отклика, а также тип ее линий уровня.
3 Штрафную и вспомогательную целевую функции.
4 Описание метода оптимизации.
5 Графическую интерпретацию поиска экстремумов с областью допустимых решений и линиями уровня целевой функции.
6 Результаты оптимизации.
7 Выводы об эффективности метода штрафных функций.
8 Текст программы для решения задачи нелинейного программирования.
адание к расчетно-графической работе 2
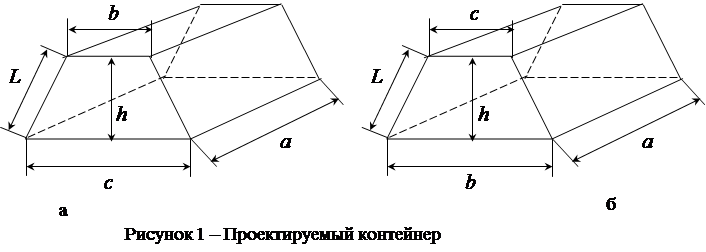
Спроектировать контейнер в форме прямой призмы, две грани которой представляют собой равнобочные трапеции, а остальные - прямоугольники (рисунок 1), емкостью V м3 таким образом, чтобы площадь его поверхности имела наименьшее значение. Дополнительные условия приведены в приложении Б.
Порядок выполнения работы
1 Используя только второе ограничение на размеры и методы дифференциального исчисления, преобразовать задачу оптимизации к решению системы уравнений. Решить полученную систему одним из известных методов. Определить оптимальные размеры контейнера.
2 Используя только второе ограничение на размеры, определить оптимальные размеры контейнера методами оптимизации. Сравнить с решением пункта 1.
3 Используя оба ограничения на размеры, определить оптимальные размеры контейнера методами оптимизации. Сравнить с решением пункта 2.
4 Оформить отчет о работе.
Содержание отчета
Отчет должен содержать:
1 Постановку задачи.
2 Расчет целевой функции и ограничений.
3 Расчет системы уравнений.
4 Описание используемых методов.
5 Оптимальные размеры контейнера по каждому из пп. 1-3.
6 Общие выводы по решению задачи оптимального проектирования.
7 Текст программы расчета оптимальных параметров, согласно пп. 1-3.
СПИСОК РЕКОМЕHДУЕМОЙ ЛИТЕРАТУРЫ
1 Акулич И.Л. Математическое программирование в примерах и задачах. - М.: Высш. шк., 1986. - 319 с.
2 Батищев Д.И. Методы оптимального проектирования. - М.: Радио и связь, 1984. - 284 с.
3 Дегтярев Ю.И. Исследование операций. - М.: Высш. шк., 1986.- 320 с.
4 Зайченко Ю.П. Исследование операций. - Киев: Выща шк.,1988. - 552 с.
5 Мину М. Математическое программирование. Теория и алгоритмы. - М.: Наука, 1990. - 488 с.
6 Норенков И.П. Введение в автоматизированное проектирование технических устройств и систем. - М.: Высш. шк.,1986. -304 с.
7 Применение математических методов и ЭВМ. Вычислительные методы проектирования оптимальных конструкций /А.Н. Останин, В.А. Гугля, Н.Н. Гурский и др. - Мн.: Выш. шк., 1989. - 279 с.
8 Системы автоматизированного проектирования. В 9 кн./Под ред. И.П. Норенкова. Кн. 5. Кузьмик П.К., Маничев В.Б. Автоматизация функционального проектирования. - Мн.: Выш. шк., 1988.-144 с.
9 Турчак Л.И. Основы численных методов. - М.: Наука, 1987. -320 с.
10 Методические указания к лабораторным работам по дисциплине "Методы синтеза и оптимизации" (для студентов специальности 7.080402)."Локальные методы безусловной оптимизации" / Сост.: Г.Б.Билык, О.В.Веремей - Краматорск: ДГМА, 2000. - 60 с.
ПРИЛОЖЕНИЯ
Приложение А
| Вар. | Условие задания | Вар. | Условие задания |
z=x 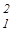 -6x1-x2 -6x1-x2 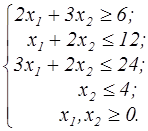 | z=(x1-3)2+(x2-4)2  | ||
z=4(x1+2)2+(x2-1)2  | z=(x1-4)2+(x2-3)2 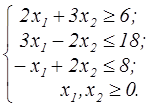 | ||
z = x1 × x2  | z=x  +x +x  -x1-8x2 -x1-8x2 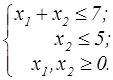 | ||
z = 4x1 - 3x2 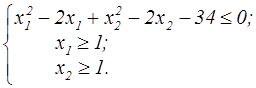 | z=x  +2x +2x  -2x1-4x2 -2x1-4x2 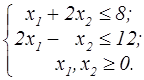 | ||
z=x  +x +x  -4x1-10x2 -4x1-10x2  | z = 3x1 - 4x2 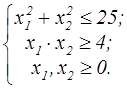 | ||
z=3(x1-1)2+6(x2-1)2 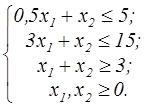 | z=2(x1-4)2+8(x2-2)2  | ||
z=2x  +x +x  -4x1-2x2 -4x1-2x2 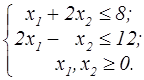 | z=x  +x +x  +2x1+2x2 +2x1+2x2  |
Продолжение приложения А
| Вар. | Условие задания | Вар. | Условие задания |
z=9(x1-5)2+2(x2-3)2 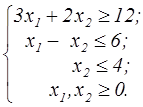 | z=x  +x +x  -2x1+4x2 -2x1+4x2 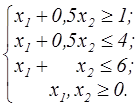 | ||
z=2x  +5x +5x  -x1-4x2 -x1-4x2 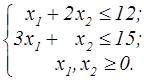 | z=x  +x +x  +2x1-8x2 +2x1-8x2  | ||
z=2(x1-6)2+6(x2-2)2  | z = x  - 4x1 - x2 - 4x1 - x2 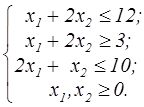 | ||
z = 8x  + 2x + 2x  +5 +5  | z = x1 × x2  | ||
z=8(x1-6)2+3(x2-4)2  | z = 5x1 + 2x2  | ||
z = 2x1 - 3x2 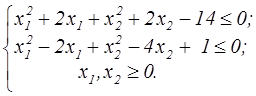 | z = 2x1 + 4x2  | ||
z=x  +x +x  -10x1-4x2 -10x1-4x2 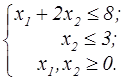 | z=x  +x +x  +4x1-2x2 +4x1-2x2 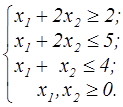 |
Продолжение приложения А
| Вар. | Условие задания | Вар. | Условие задания |
z=(x1-3)2+4(x2-5)2 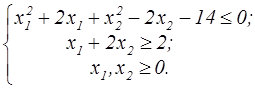 | z=x  +x +x  -8x1-x2 -8x1-x2  | ||
z=4(x1+2)2+(x2-1)2 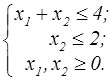 | z=(x1-3)2+(x2-4)2 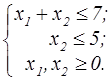 | ||
z = 4x1 + 3x2 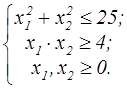 | z = 3x1 + 4x2 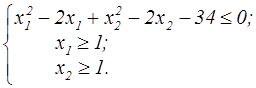 | ||
z=x  -6x1-x2 -6x1-x2 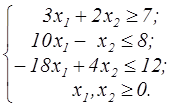 | z=(x1-4)2+(x2-3)2  | ||
z = x1 × x2 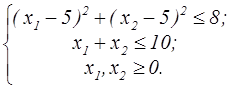 | z=x  +2x +2x  -2x1-4x2 -2x1-4x2 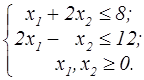 | ||
z=x  +x +x  -x1-8x2 -x1-8x2 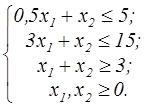 | z=x  +x +x  -4x1-10x2 -4x1-10x2 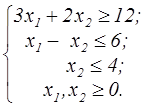 | ||
z=3(x1-1)2+6(x2-1)2 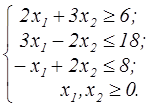 | z=8(x1-6)2+3(x2-4)2 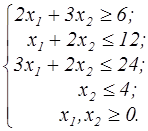 |
Продолжение приложения А
| Вар. | Условие задания | Вар. | Условие задания |
z=2(x1-4)2+8(x2-2)2  | z=x  +x +x  +2x1+2x2 +2x1+2x2 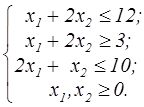 | ||
z = 2x1 + 3x2 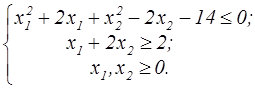 | z = 2x1 + 4x2 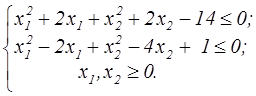 | ||
z=9(x1-5)2+2(x2-3)2 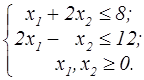 | z=x  +2x +2x  -2x1-4x2 -2x1-4x2 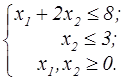 | ||
z=2x  +5x +5x  -x1-4x2 -x1-4x2  | z = x  - 4x1 - x2 - 4x1 - x2  | ||
z = 8x  + 2x + 2x  +5 +5 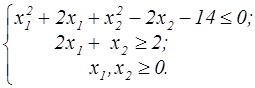 | z=2(x1-6)2+6(x2-2)2  | ||
z=x  +x +x  -10x1-4x2 -10x1-4x2 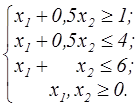 | z=x  +x +x  -8x1-x2 -8x1-x2 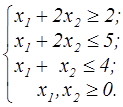 | ||
z=x  +x +x  +2x1-8x2 +2x1-8x2 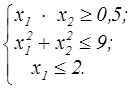 | z = x1 × x2  |
Продолжение приложения А
| Вар. | Условие задания | Вар. | Условие задания |
z=x  +x +x  -2x1+4x2 -2x1+4x2  | z=(x1-3)2+4(x2-5)2  | ||
z=x  +x +x  +4x1-2x2 +4x1-2x2  | z = 5x1 + 2x2 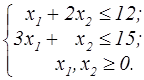 | ||
z=x 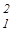 -6x1-x2 -6x1-x2  | z=4(x1+2)2+(x2-1)2 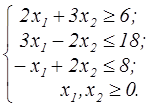 | ||
z=x  +2x +2x  -2x1-4x2 -2x1-4x2  | z = 4x1 + 3x2 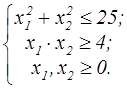 | ||
z=3(x1-1)2+6(x2-1)2  | z=2(x1-4)2+8(x2-2)2 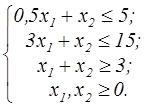 | ||
z=x  +x +x  +2x1+2x2 +2x1+2x2 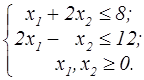 | z=x  +2x +2x  -2x1-4x2 -2x1-4x2  | ||
z=x  +x +x  -2x1+4x2 -2x1+4x2 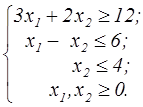 | z=2x  +5x +5x  -x1-4x2 -x1-4x2 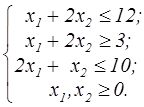 |
Продолжение приложения А
| Вар. | Условие задания | Вар. | Условие задания |
z=x  +x +x  +2x1-8x2 +2x1-8x2  | z = x  - 4x1 - x2 - 4x1 - x2  | ||
z=2(x1-6)2+6(x2-2)2  | z = 8x  + 2x + 2x  +5 +5 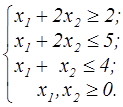 | ||
z=8(x1-6)2+3(x2-4)2  | z = 5x1 + 2x2 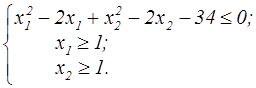 | ||
z = 2x1 + 3x2  | z = 2x1 + 4x2 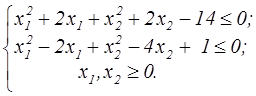 | ||
z=x  +x +x  -10x1-4x2 -10x1-4x2 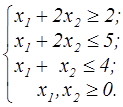 | z=x  +x +x  -8x1-x2 -8x1-x2 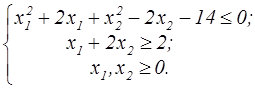 |
Приложение Б
| Вариант | Поверхность контейнера | Объем V | Ограничения на размеры | Рис. |
| Полная | h ³ 1.3; c/b =2 | а | ||
| без нижней грани | h ³ 1.1; c/b =2 | а | ||
| без верхней грани | L ³ 1.3; c/b =3 | а | ||
| без передней стенки | L ³ 1.8; b/c =3 | б | ||
| без правой стенки | h ³ 1.5; b/c =2 | б | ||
| Полная | h ³ 1.4; b/c =2 | б | ||
| без нижней грани | L ³ 1.5; c/b =3 | а | ||
| без верхней грани | L ³ 1.7; c/b =3 | а | ||
| без передней стенки | h ³ 2.0; c/b =2 | а | ||
| без правой стенки | h ³ 1.9; b/c =2 | б | ||
| Полная | L ³ 2.0; b/c =3 | б | ||
| без нижней грани | L ³ 1.8; b/c =3 | б | ||
| без верхней грани | h ³ 1.5; c/b =2 | а | ||
| без передней стенки | h ³ 2.2; c/b =2 | а | ||
| без правой стенки | L ³ 2.4; c/b =3 | а | ||
| Полная | L ³ 2.3; b/c =3 | б | ||
| без нижней грани | h ³ 1.6; b/c =2 | б | ||
| без верхней грани | h ³ 1.8; b/c =2 | б | ||
| без передней стенки | L ³ 2.8; c/b =3 | а | ||
| без правой стенки | L ³ 2.9; c/b =3 | а | ||
| Полная | h ³ 2.4; c/b =2 | а | ||
| без нижней грани | h ³ 1.6; b/c =2 | б | ||
| без верхней грани | L ³ 2.5; b/c =3 | б | ||
| без передней стенки | L ³ 2.8; b/c =3 | б | ||
| без правой стенки | h ³ 1.5; c/b =2 | а | ||
| Полная | h ³ 1.6; c/b =3 | а | ||
| без нижней грани | L ³ 1.7; c/b =3 | а | ||
| без верхней грани | L ³ 1.8; b/c =2 | б | ||
| без передней стенки | h ³ 1.6; b/c =2 | б | ||
| без правой стенки | h ³ 1.7; b/c =3 | б | ||
| Полная | L ³ 1.9; c/b =3 | а | ||
| без нижней грани | L ³ 1.5; c/b =2 | а | ||
| без верхней грани | h ³ 1.6; c/b =2 | а | ||
| без передней стенки | h ³ 2.2; b/c =3 | б | ||
| без правой стенки | L ³ 2.4; b/c =3 | б | ||
| Полная | L ³ 1.9; b/c =2 | б | ||
| без нижней грани | h ³ 1.6; c/b =2 | а |
Продолжение приложения Б
| Вариант | Поверхность контейнера | Объем V | Ограничения на размеры | Рис. |
| без верхней грани | h ³ 2.1; c/b =3 | а | ||
| без передней стенки | L ³ 2.8; c/b =3 | а | ||
| без правой стенки | L ³ 2.4; b/c =2 | б | ||
| Полная | h ³ 1.9; b/c =2 | б | ||
| без нижней грани | h ³ 1.7; b/c =3 | б | ||
| без верхней грани | L ³ 2.4; c/b =3 | а | ||
| без передней стенки | L ³ 2.8; c/b =2 | а | ||
| без правой стенки | h ³ 2.5; c/b =2 | а | ||
| Полная | h ³ 2.4; b/c =3 | б | ||
| без нижней грани | L ³ 1.9; b/c =3 | б | ||
| без верхней грани | L ³ 2.0; b/c =2 | б | ||
| без передней стенки | h ³ 2.3; c/b =2 | а | ||
| без правой стенки | h ³ 2.5; c/b =3 | а | ||
| Полная | L ³ 2.1; c/b =3 | а | ||
| без нижней грани | L ³ 2.5; b/c =2 | б | ||
| без верхней грани | h ³ 2.0; b/c =3 | б | ||
| без передней стенки | h ³ 2.2; b/c =3 | б | ||
| без правой стенки | L ³ 2.8; c/b =2 | а | ||
| Полная | L ³ 2.6; c/b =2 | а | ||
| без нижней грани | h ³ 2.5; c/b =3 | а | ||
| без верхней грани | h ³ 2.4; b/c =3 | б | ||
| без передней стенки | L ³ 1.9; b/c =2 | б | ||
| без правой стенки | L ³ 2.0; b/c =2 | б | ||
| Полная | h ³ 3.4; c/b =4 | а | ||
| без нижней грани | h ³ 3.1; c/b =3 | а | ||
| без верхней грани | L ³ 3.3; c/b =4 | а | ||
| без передней стенки | L ³ 3.8; b/c =4 | б | ||
| без правой стенки | h ³ 3.5; b/c =2 | б | ||
| Полная | h ³ 3.4; b/c =3 | б | ||
| без нижней грани | L ³ 3.5; c/b =2 | а | ||
| без верхней грани | L ³ 3.7; c/b =3 | а | ||
| без передней стенки | h ³ 3.0; c/b =3 | а | ||
| без правой стенки | h ³ 2.9; b/c =3 | б | ||
| Полная | L ³ 3.0; b/c =2 | б | ||
| без нижней грани | L ³ 2.8; b/c =3 | б | ||
| без верхней грани | h ³ 2.5; c/b =4 | а | ||
| без передней стенки | h ³ 2.7; c/b =3 | а |
Продолжение приложения Б
| Вариант | Поверхность контейнера | Объем V | Ограничения на размеры | Рис. |
| без правой стенки | L ³ 2.9; c/b =3 | а | ||
| Полная | L ³ 3.3; b/c =3 | б | ||
| без нижней грани | h ³ 1.9; b/c =4 | б | ||
| без верхней грани | h ³ 2.3; b/c =3 | б | ||
| без передней стенки | L ³ 2.4; c/b =2 | а | ||
| без правой стенки | L ³ 2.8; c/b =3 | а |
СОДЕРЖАHИЕ
Введение......................................…………………………………………….. 3
Задания к расчетно-графическим работам........……………………………. 3
Задания к расчетно-графической работе 1.......…………………………….. 3
Задания к расчетно-графической работе 2......……………………………... 4
Список рекомендуемой литературы...............……………………………… 5
Приложения...................................……………………………………..……. 5
Приложение А..................................…………………………………………. 6
Приложение Б..................................………………………………………… 12
Методические указания
к расчетно-графическим работам по дисциплине
"Методы синтеза и оптимизации"
(для студентов специальности 7.080402)
Составители: Григорий Борисович Билык
Ольга Владимировна Веремей
