Дивергенция электрического поля

Закон Кулона.

Основой электростатики является закон Кулона (1785 г.). В современной формулировке он устанавливает силу взаимодействия двух неподвижных точечных зарядов.

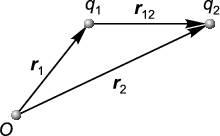
Рис. 1.1: Закон Кулона формулируется для двух точечных зарядов

Согласно закону Кулона, электрический заряд q1, находящийся в точке с радиус вектором r→1, действует на заряд q2 в точке с радиус вектором r→2 с силой F→12 = q1q2 r→2 −r→1 ∣r→2 −r→1∣3. (1.1)

По третьему закону Ньютона, сила, действующая на первый заряд со стороны второго, имеет противоположный знак, т.е.

F→21 = −F→12 = q1q2 r→1 −r→2 ∣r→1 −r→2∣3 .

Закон Кулона (1.1) записан в абсолютной гауссовой системе единиц, которую также называют системой СГС. В электродинамике от выбора системы единиц зависит даже сам вид формул. Например, в системе СИ в законе Кулона появляется дополнительный коэффициент, имеющий не только числовое значение, но и размерность. В нашей книге мы повсеместно используем систему СГС. Правила пересчета систем единиц изложены в приложении A. Там же имеется сводка ключевых формул электродинамики в системе СИ. Система СГС удобна для теоретических расчетов, но на практике чаще применяют систему СИ. Многие физики делают промежуточные вычисления в системе СГС и лишь окончательный результат переводят в систему СИ. Для этого достаточно знать несколько приближенных соотношений между единицами СГС и СИ.

В системе СГС сила измеряется в динах (дн), расстояние в сантиметрах, а заряд — в статкулонах (стКл): [q] = 1стКл = 1г1∕2 см3∕2∕сек. (1.2)

Заряд величиной 1стКл, находящийся на расстоянии 1см от равного себе, действует на него с силой 1дн. В системе СИ единицей измерения заряда является Кулон (Кл). Это очень большая величина: 1Кл ≈ 3⋅109 стКл. (1.3)

На расстоянии 1 метр он действует на равный себе с силой 9⋅1013 н.

Электрический заряд.

Что такое заряд? Философ бы ответил, что это некая характеристика реального мира, данного нам в ощущение. Нам известно, что некоторые материальные объекты притягиваются или отталкиваются с силой, пропорциональной квадрату расстояния между ними. Это свойство таких объектов характеризуется тем, что таким объектам приписывается электрический заряд.

Известно, что существуют заряды двух сортов (Бенджамин Франклин, 1706–1790; 1747г.), так как заряды могут отталкиваться, а могут притягиваться. Известно также, что заряды одного сорта отталкиваются. Если бы это было не так, к закону Кулона (1.1) пришлось бы приписать знак минус. Замена притяжения отталкиванием есть просто смена знака силы. Из закона Кулона явствует, что сила изменяет направление при изменении знака заряда. Следовательно, два сорта зарядов — это заряды положительные и заряды отрицательные. Сейчас этому учат в школе и трудно представить, что ещё не так давно люди этого не знали.

Какой сорт зарядов считать положительным, а какой отрицательным — дело соглашения. История распорядилась так, что заряд электрона считают отрицательным, а заряд протона — положительным.

Величину заряда определяют при помощи закона Кулона. Выбрав какой-то заряд в качестве эталона, можно определить знак другого заряда и во сколько раз по абсолютной величине он больше или меньше эталонного. Природный эталон заряда называют элементарным зарядом; по абсолютной величине он равен заряду электрона, поэтому его обозначают буквой e. Однако элементарный заряд слишком мал, чтобы его удобно было считать единицей измерения. В системе СГС e = (4,803242 ± 0,000014)⋅10−10стКл; в системе СИ e = (1,6021892 ± 0,0000046)⋅10−19Кл.

Современная наука считает элементарный заряд величиной, не зависящей от времени, т.е. мировой константой. Существуют теории, согласно которым некоторые мировые константы изменяются в ходе эволюции Вселенной. Однако относительно элементарного заряда достоверных сведений такого рода нет. Отсюда следует закон сохранения заряда в замкнутой системе: Q = ∑ iqi = const. (2.1)

Он остается в силе, даже если число заряженных частиц изменяется за счёт реакций между ними, как, например, при аннигиляции электрона и позитрона:

e−e+ → 2γ .

Важно только, чтобы заряды не пересекали границы объема; в противном случае объем не является замкнутым.

Электрическое поле.

Закон Кулона предстанет в совершенно ином свете, если ввести понятие электрического поля. Зафиксируем в пространстве заряд q1. Для простоты можно считать, что он расположен в начале координат, а радиус-вектор точки, где расположен второй, так называемый пробный заряд q2, обозначить через r→ (без индекса).

Рис. 1.2: К определению понятия электрического поля

Если теперь в законе Кулона (1.1) вынести величину пробного заряда в буквальном смысле за скобки, F→12 = q2 q1 r2 r→ r ≡ q2 E→1(r→), (3.1)

то выяснится, что нечто, оставшееся в скобках, можно измерить в простом опыте, если заранее знать величину пробного заряда q2. Для этого достаточно измерить направление и величину силы, действующей на пробный заряд. Перемещая пробный заряд, измерения можно выполнить, по крайней мере мысленно, во всех точках пространства. Таким образом, нечто, обозначенное выше через E1(r→), является тем, что в математике принято называть векторным полем. В данном случае это электрическое поле. Существенно, что оно не зависит от пробного заряда. Можно сказать, что заряд q1 создает в окружающем пространстве электрическое поле независимо от того, имеется ли ещё какой-либо заряд, в том числе пробный, или его нет. Электрическое поле может быть создано зарядом другой величины, расположенным в другом месте, или даже несколькими зарядами одновременно. Если оно известно, то известна и сила, действующая на пробный заряд. По сути дела, определением электрического поля является равенство F→ = q E→, (3.2)

где q — величина пробного заряда, а F→ — сила, действующая на него в точке r→. Из закона Кулона следует, что электрическое поле точечного заряда q на расстоянии r→ от него равно E→(r→) = q r2 r→ r. (3.3)

В зависимости от постановки задачи один и тот же заряд q можно рассматривать в качестве источника поля (3.3) или в качестве инструмента измерения поля других зарядов, как следует из (3.2). Вектор E→ называют вектором напряженности электрического поля, или просто электрическим полем. Абсолютное значение E = ∣E→∣ вектора E→ называют напряженностью электрического поля.

Формулировка закона Кулона в виде (1.1) соответствует так называемой концепции дальнодействия. Согласно ей, взаимодействие зарядов, находящихся на расстоянии друг от друга, осуществляется без промежуточной субстанции, которую в прошлом отождествляли с мировым эфиром. Представление закона Кулона в виде (3.3) соответствует концепции близкодействия, когда силовое воздействие на заряд способны оказывать только упругие напряжения мирового эфира. Концепция близкодействия более адекватна современной трактовке взаимодействия частиц посредством переноса квантов поля, но в целом представления о мировом эфире безнадежно устарели.

В рамках электростатики электрическое поле остается не более чем формальным, математическим понятием. Исследуя только статические явления, невозможно сделать однозначный выбор между концепциями дально- и близкодействия. Только электродинамика, доказывающая существование электромагнитных волн, делает электрическое поле физической реальностью. Понять это утверждение можно хотя бы на примере упоминавшейся уже реакции аннигиляции электрон-позитронной пары:

e−e+ → 2γ .

В результате аннигиляции исчезают заряженные частицы — источники электрического поля, но зато возникает свободное электромагнитное поле в виде двух гамма-квантов.

Принцип суперпозиции.

Если E→1(r→) — поле системы зарядов №1, а E→2(r→) — поле системы зарядов №2, то при наличии зарядов обоих систем E→(r→) = E→1(r→) + E→2(r→). (4.1)

Рис. 1.3 поясняет сказанное.

Рис. 1.3: Принцип суперпозиции. В отсутствие заряда q2 на пробный заряд q3 действует сила F→13 = q3E→1, а в отсутствие заряда q1 — сила F→23 = q3E→2. При наличии обоих зарядов действующая сила равна их сумме, F→3 = F→13 + F→23 = q3E→. Отсюда следует, что в месте нахождения пробного заряда E→ = E→1 + E→2.

Простейшая система состоит из одного заряда. Следовательно, электрическое поле системы зарядов равно сумме полей, создаваемых каждым зарядом в отдельности, в отсутствие других зарядов: E→(r→) = ∑ j qj ∣r→ −r→j∣2 r→ −r→j ∣r→ −r→j∣. (4.2)

Здесь qj,r→j — заряд и радиус-вектор j-го заряда. Правило сложения (4.1) называют принципом суперпозиции, а формула (4.2) является следствием принципа суперпозиции и закона Кулона.

Принцип суперпозиции является экспериментальным фактом. В электродинамике он рассматривается как абсолютно точный в том смысле, что никакие отклонения от него не обнаружены. Принцип суперпозиции для электрического поля не столь очевиден, как могло бы показаться на первый взгляд. Например, можно предположить, что он нарушается в очень сильном поле аналогично тому, как в твердом теле упругие напряжения можно складывать только при условии, что они достаточно малы (при больших деформациях тело разрушается). Однако эксперименты свидетельствуют, что даже на поверхности тяжёлых ядер, где электрическое поле достигает громадных значений, принцип суперпозиции выполняется. Другое дело, что при полях, примерно в 100 раз меньших, проявляются эффекты поляризации вакуума в результате рождения электрон-позитронных пар. Это приводит к квантово-механической нелинейности взаимодействия зарядов.

Теорема Гаусса.

Принцип суперпозиции в сочетании с законом Кулона даёт ключ к вычислению электрического поля произвольной системы зарядов, но непосредственное суммирование полей по формуле (4.2) обычно требует сложных вычислений. Впрочем, при наличии той или иной симметрии системы зарядов вычисления существенно упрощаются, если ввести понятие потока электрического поля и использовать теорему Гаусса.

Представления о потоке электрического поля привнесены в электродинамику из гидродинамики. В гидродинамике поток жидкости через трубу, то есть объём жидкости N, проходящий через сечение трубы в единицу времени, равен v⋅S, где v — скорость жидкости, а S — площадь сечения трубы. Если скорость жидкости изменяется по сечению, нужно использовать интегральную формулу N = ∫ Sv→⋅dS→. Действительно, выделим в поле скоростей малую площадку dS, перпендикулярную к вектору скорости (рис. 1.4).

Рис. 1.4: Поток жидкости

Объём жидкости, протекающий через эту площадку за время dt, равен v dS dt. Если площадка наклонена к потоку, то соответствующий объём будет v dScosθdt, где θ — угол между вектором скорости v→ и нормалью n→ к площадке dS. Объём жидкости, протекающий через площадку dS в единицу времени получается делением этой величины на dt. Он равен v dS cosθdt, т.е. скалярному произведению v→⋅dS→ вектора скорости v→ на вектор элемента площади dS→ = n→dS. Единичный вектор n→ нормали к площадке dS можно провести в двух прямо противоположных направлениях. одно из них условно принимается за положительное. В этом направлении и проводится нормаль n→. Та сторона площадки, из которой выходит нормаль n→, называется внешней, а та, в которую нормаль n→ входит, — внутренней. Вектор элемента площади dS→ направлен по внешней нормали n→ к поверхности, а по величине равен площади элемента dS = ∣dS→∣. При вычислении объёма протекающей жидкости через площадку S конечных размеров, её надо развить на бесконечно малые площадки dS, а затем вычислить интеграл ∫ Sv→⋅dS→ по всей поверхности S.

Выражения типа ∫ Sv→⋅dS→ встречаются во многих отраслях физики и математики. Они называются потоком вектора v→ через поверхность S независимо от природы вектора v→. В электродинамике интеграл N = ∫ SE→⋅dS→ (5.1)

называют потоком напряженности электрического поля E→ через произвольную поверхность S, хотя с этим понятием не связано никакое реальное течение.

Допустим, что вектор E→ представляется геометрической суммой

E→ = ∑ jE→j .

Умножив это равенство скалярно на dS→ и проинтегрировав, получим

N = ∑ jNj .

где Nj — поток вектора E→j через ту же самую поверхность. Таким образом, из принципа суперпозиции напряженности электрического поля следует, что потоки через одну и ту же поверхность складываются алгебраически.

Теорема Гаусса гласит, что поток вектора E→ через произвольную замкнутую поверхность равен умноженному на 4π суммарному заряду Q всех частиц, находящихся внутри этой поверхности: ∮ SE→⋅dS→ = 4πQ. (5.2)

Вектор элемента поверхности dS→ здесь направлен по нормали, внешней по отношению к тому объему, где сосредоточен заряд Q (рис. 1.5).

Рис. 1.5: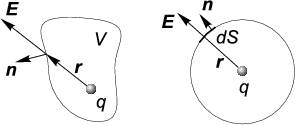

Теорема Гаусса для одного точечного заряда

Доказательство теоремы проведем в три этапа.

1. Начнем с вычисления потока электрического поля одного точечного заряда q (рис. 1.5). В простейшем случае, когда поверхность интегрирования S является сферой, а заряд находится в её центре, справедливость теоремы Гаусса практически очевидна. На поверхности сферы напряженность электрического поля

E→ = qr→∕r3

постоянна по величине и всюду направлена по нормали к поверхности, так что поток электрического поля просто равен произведению E = q∕r2 на площадь сферы S = 4πr2. Следовательно, N = 4πq. Этот результат не зависит от формы поверхности, окружающей заряд. Чтобы доказать это, выделим произвольную площадку поверхности достаточно малого размера с установленным на ней направлением внешней нормали n→. На рис. 1.6 показан один такой сегмент преувеличенно большого (для наглядности) размера.

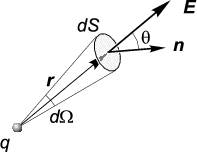
Рис. 1.6: Поток электрического в элемент телесного угла

Поток вектора E→ через эту площадку равен

dN = E→⋅dS→ = EcosθdS ,

где θ — угол между направлением E→ и внешней нормалью n→ к площадке dS. Так как E = q∕r2, а dScosθ∕r2 по абсолютной величине есть элемент телесного угла dΩ = dS∣cosθ∣∕r2, под которым видна площадка dS из точки расположения заряда,

dN = ±q dΩ.

где знаки плюс и минус отвечают знаку cosθ, а именно: следует взять знак плюс, если вектор E→ составляет острый угол с направлением внешней нормали n→, и знак минус в противном случае.

2. Теперь рассмотрим конечную поверхность S, охватывающую некоторый выделенный объём V . По отношению к этому объёму всегда можно определить, какое из двух противоположных направлений нормали к любому элементу поверхности S следует считать внешним. Внешняя нормаль направлена из объёма V наружу. Суммируя по сегментам, с точностью до знака имеем N = q Ω, где Ω — телесный угол, под которым видна поверхность S из точки, где находится заряд q. Если поверхность S замкнута, то Ω = 4π при условии, что заряд q находится внутри S. В противном случае Ω = 0. Чтобы пояснить последнее утверждение, можно вновь обратиться к рис. 1.7.

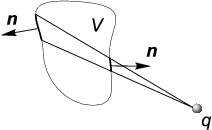
Рис. 1.7: Потоки через площадки, опирающиеся на один телесный угол, но обращенные в разные стороны, взаимно сокращаются.

Очевидно, что потоки через сегменты замкнутой поверхности, опирающиеся на равные телесные углы, но обращенные в противоположные стороны, взаимно сокращаются. Очевидно также, что если заряд находится вне замкнутой поверхности, то любому сегменту, обращенному наружу, найдется соответствующий сегмент, обращенный внутрь.

3. Наконец, воспользовавшись принципом суперпозиции, приходим к итоговой формулировке теоремы Гаусса (5.2). Действительно, поле системы зарядов равно сумме полей каждого заряда в отдельности, но в правую часть теоремы (5.2) дают ненулевой вклад только заряды, находящиеся внутри замкнутой поверхности. Этим завершается доказательство.

В макроскопических телах число носителей заряда столь велико, что дискретный ансамбль частиц удобно представить в виде непрерывного распределения, введя понятие плотности заряда. По определению, плотностью заряда ρ называется отношение ΔQ∕ΔV в пределе, когда объём ΔV стремится к физически бесконечно малой величине: ρ = limΔV →0ΔQ ΔV = dQ dV. (5.3)

Физически бесконечно малым является объём, который мал по сравнению с любыми другими макроскопическими размерами рассматриваемой задачи, но достаточно велик по сравнению с расстоянием между частицами, в данном случае заряженными частицами. С помощью плотности заряда теорему Гаусса можно переписать в виде ∮ SE→⋅dS→ = 4π ∫ V ρdV, (5.4)

где интегрирование в правой части производится по объему V , замкнутому поверхностью S.

Теорема Гаусса даёт одно скалярное уравнение на три компоненты вектора E→, поэтому для расчета электрического поля одной этой теоремы недостаточно. Необходима известная симметрия распределения плотности зарядов, чтобы задача могла быть сведена к одному скалярному уравнению. Теорема Гаусса позволяет найти поле в тех случаях, когда поверхность интегрирования в (5.4) удается выбрать так, что напряженность электрического поля E постоянна на всей поверхности.

Дивергенция электрического поля.

С помощью теоремы Остроградского поверхностный интеграл в левой части теоремы Гаусса (5.4) можно преобразовать в интеграл по объему V , ограниченному поверхностью S: ∮ SE→⋅dS→ = ∫ V divE→dV. (6.1)

Результат преобразования называют теоремой Остроградского-Гаусса: ∫ V divE→dV = 4π ∫ V ρdV .

Поскольку она верна для любой области интегрирования V , в том числе и бесконечно малой, из неё следует равенство подынтегральных выражений слева и справа в каждой точке пространства: divE→ = 4πρ. (6.2)

Это дифференциальное уравнение является одним из основных уравнений электростатики; оно верно также для динамических явлений.

Теорему Остроградского (6.1) можно пытаться доказывать, отталкиваясь от какого-либо из определений оператора дивергенции div. Однако саму эту теорему можно рассматривать в качестве инвариантного определения div, не зависящего от выбора системы координат. Переходя в (6.1) к пределу V → 0, получаем: divE→ = limV →0 ∮ SE→⋅dS→ V. (6.3)

Вместо E→ здесь, как и в (6.1), может стоять любой другой вектор.

Покажем, как из (6.3) получается выражение для дивергенции в декартовых координатах. Рассмотрим небольшой параллепипед, образованный координатными плоскостями, как показано на рис. 1.12.

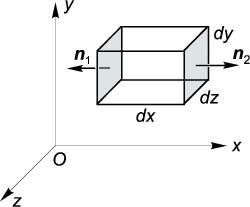
Рис. 1.12:

В пределах каждой грани параллелипипеда вектор E→ можно считать постоянным, поскольку затем размеры параллелипипеда будут устремлены к нулю. Тогда поверхностный интеграл по каждой грани равен произведению площади грани на нормальную (к этой грани) компоненту вектора E→. Например, для пары противоположных граней в координатных плоскостях x и x + dx имеем (Ex∣x+dx − Ex∣x)∣Sx∣, где ∣Sx∣ = dy dz — площадь каждой из граней. Знак минус перед вторым слагаемым в скобках здесь связан с тем, что нормаль к соответствующей грани направлена в отрицательном направлении оси x. Разлагая первое слагаемое в скобках в ряд Тейлора вокруг точки x с точностью до члена, линейного по dx, находим, что вклад этой пары граней в поверхностный интеграл равен (∂Ex∕∂x)V , где V = dxdy dz. Аналогичным образом вычисляется вклад двух других пар граней. После сокращения на V из (6.3) получаем: divE→ = ∂Ex ∂x + ∂Ey ∂y + ∂Ez ∂z . (6.4)