Пример игры с седловой точкой. Конфликт интересов при дуополии

Две фирмы А и В делят рынок некоторого товара. У каждой фирмы разработаны по 3 варианта действия по расширению рынка. Захват некоторой доли рынка означает соответствующее уменьшение доли другой фирмы. Платежная матрица показывает увеличение доли фирмы А в % (уменьшение доли фирмы В на столько же %) в зависимости от применяемых фирмами А и В стратегий. Например: элемент a₃₂=2 означает, что при использовании первой фирмой третьего плана ( третьей стратегии) и второй фирмой второй стратегии 2% рынка перейдут первой фирме, т.е. доля рынка фирмы А увеличится на 2%, а фирмы В уменьшится на 2%. Цель каждой фирмы – максимально возможное увеличение своей доли на рынке. Найти оптимальную стратегию для каждой фирмы.

4
	4

► Для первого игрока находим наименьший элемент в каждой строке, из этих наихудших результатов выбираем наибольший. Это нижняя цена игры =4. Для второго игрока наихудшим результатом применения стратегии будет наибольший элемент (проигрыш) в столбце. Наименьший из них равен 4 - верхняя цена игры. Нижняя и верхняя цена игры совпадают. Задача имеет седловую точку a₂₂=4, значит цена игры v=4, пара оптимальных стратегий (А₂, В₂). Фирма А выбирает второй план расширения рынка и фирма В – второй. При этом фирма А увеличивает свою долю рынка на 4%. Каждый из игроков должен придерживаться своей оптимальной чистой стратегии. Любое отклонение от неё будет невыгодно для игрока, допустившего отклонение. ◄

Часто платежную матрицу удается упростить, удалив из неё строки и столбцы, соответствующие дублирующим и доминируемым стратегиям игроков. Стратегии называются дублирующими, если соответствующие им строки (столбцы) одинаковы. Доминируемой называется стратегия, все платежи которой не лучше соответствующих платежей другой стратегии и хотя бы один из платежей хуже соответствующего платежа этой другой стратегии, называемой доминирующей. В отдельных случаях из множества чистых стратегий удается удалить все, кроме одной, она и будет оптимальной.

Пример. Упростим платежную матрицу, вычеркивая доминируемые (заведомо невыгодные) стратегии.

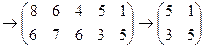
Вторая и четвертая стратегии первого игрока хуже третьей, т.к. при любом поведении второго игрока выигрыши меньше. Поэтому удалим вторую и четвертую строки. Далее видим, что первые три стратегии второго игрока менее удачные, чем пятая, т.к. проигрыши больше, удалим первый, второй и третий доминируемые столбцы. Осталась платежная матрица 2х2. Найдем нижнюю цену игры – наилучший среди наихудших платежей первому игроку. По строкам минимальные элементы 1 и 3, наибольший из них 3. Определяя верхнюю цену игры, найдем максимальные (наиболее неблагоприятные для второго игрока) платежи по столбцам: оба 5. Нижняя цена игры 3 меньше верхней цены 5. Это означает, что седловая точка отсутствует. ◄