Точечная оценка коэффициента корреляции

Мы начнем проведение корреляционного анализа со статистического анализа коэффициента корреляции. Этот показатель имеет четкий смысл как характеристика степени связи между исследуемыми случайными величинами X и Y только в случае их совместного нормального распределения. Во всех остальных случаях коэффициент корреляции можно использовать лишь в качестве одной из возможных характеристик степени тесноты связи. В этом случае нужно подходить с известной долей осторожности к интерпретации корреляционной связи на основе только коэффициента корреляции. Однако в силу закона больших чисел (в широком смысле) нормальное распределение встречается довольно часто, а следовательно и использование коэффициента корреляции в качестве характеристики тесноты связи во многих случаях вполне оправдано.

На практике коэффициент корреляции r_xy обычно неизвестен. По результатам выборочных данных может быть найдена лишь его точечная оценка – выборочный коэффициент корреляции r_xy. Для его нахождения необходимо знать оценки математических ожиданий, дисперсий и ковариации случайных величин X и Y. Наилучшей оценкой математического ожидания является среднее арифметическое выборочных данных

. (4.21)

Оценкой дисперсии служит исправленная выборочная дисперсия:

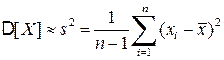, (4.22)

а ковариации – исправленная выборочная ковариация:

. (4.23)

Тогда выборочный коэффициент корреляции будет иметь вид

. (4.24)

На практике чаще используется следующая модифицированная формула для вычисления выборочного коэффициента корреляции:

, (4.25)

где – обычные (неисправленные) выборочные средние квадратичные отклонения.

Если коэффициент корреляции положителен r_xy>0, то связь между X и Y будет прямая, если r_xy<0, то связь будет обратной. Чем ближе значение r_xy к единице, тем теснее связь, чем ближе значение r_xy к нулю, тем слабее связь. При |r|<0,3 корреляционная связь считается слабой, при 0,3<|r|<0,7 – средней, при |r|>0,7 – сильной. Отметим еще раз, что использование коэффициента корреляции как меры связи между случайными величинами имеет четко определенный смысл только для нормальных или близких к ним распределений. Поэтому, если коэффициент корреляции близок к нулю, то это означает, что либо случайные величины независимы (для нормального распределения), либо между ними имеется существенно нелинейная корреляционная зависимость. Однако, если коэффициент корреляции по модулю близок к единице, то между случайными величинами имеется сильная корреляционная, близкая к линейной функциональной, зависимость, независимо от вида функции распределения.

Пример 4.1. Изучается зависимость цены товара от дальности его перевозок по 7 фирмам. Данные представлены в табл. 4.1.

Таблица 4.1

Номер фирмы	Дальность перевозки, км, x	Цена товара, руб., y	Номер фирмы	Дальность перевозки, км, x	Цена товара, руб., y

Рассчитать линейный коэффициент парной корреляции. Сделать выводы.

Решение. Строим расчетную таблицу

Таблица 4.2

	x	y	xy	x2	y2
Итого

По данным таблицы находим:

;	;
;	;
.

Тогда

;	;
;	;
.

В результате получаем,

.

Полученное значение коэффициента корреляции показывает, что связь между ценой данного товара и дальностью его перевозки является очень сильной. â