Законы логики (свойства логических операций)

Следующие формулы являются законами логики.

1. - закон двойного отрицания.

2. - закон коммутативности конъюнкции.

3. - закон коммутативности дизъюнкции.

4. 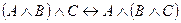- закон ассоциативности конъюнкции.

5. - закон ассоциативности дизъюнкции.

6. - закон дистрибутивности конъюнкции относительно дизъюнкции.

7. - закон дистрибутивности дизъюнкции относительно конъюнкции.

8. - закон отрицания дизъюнкции.

9. - закон отрицания конъюнкции.

10. - закон отрицания импликации.

11. 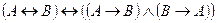- закон выражения эквивалентности через конъюнкцию и импликацию.

12. - закон контрапозиции.

13. - закон силлогизма.

Для доказательства любого из приведенных выше законов можно использовать следующие способы:

1. Построить таблицы истинности для левых и правых частей эквивалентности и убедиться, что получены одинаковые значения для всех значений атомов.

2. Построить значение всей формулы и убедится, что формула является тавтологией.

Пример. Докажем закон отрицания конъюнкции ( ) этими способами:

1. Найдем значения для 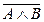и 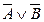и сравним их.

A	B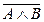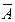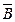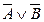
И	И	И	Л	Л	Л	Л
И	Л	Л	И	Л	И	И
Л	И	Л	И	И	Л	И
Л	Л	Л	И	И	И	И

2. Найдем значение и убедимся, что при всех значениях A и B - это истинное значение.

A	B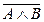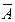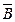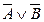
И	И	И	Л	Л	Л	Л	И
И	Л	Л	И	Л	И	И	И
Л	И	Л	И	И	Л	И	И
Л	Л	Л	И	И	И	И	И

Логическое следствие

Определение. Формула B есть логическое следствие формул A₁, A₂, .., A_n, если формула B принимает истинное значение при тех же значениях, при которых истинна каждая из формул A₁, A₂, .., A_n.

Запись (A₁, A₂, .., A_n)ÞB означает, что B – логическое следствие формул A₁, A₂, .., A_n.

Пример. (A®B, A® 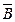)Þ .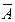

Докажем данное следствие.

A	B	A®B		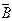A®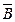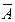
И	И	И	Л	Л	Л
И	Л	Л	И	И	Л
Л	И	И	Л	И	И
Л	Л	И	И	И	И

Из определения следует, что противоречие логически влечет любую формулу, а тавтология логически следует из любой формулы логики.

Определение. Формулы F и G называются равносильными, если они являются логическими следствиями друг друга. Обозначение: .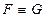

Проанализировав последнее определение, получаем, что формулы равносильны, если они на всех наборах значений переменных превращаются в одинаковые по истинностному значению высказывания.

Следующие теоремы связывают логическое следствие и импликацию, равносильность и эквиваленцию.

Теорема₁. 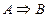тогда и только тогда, когда A®B – тавтология.

Теорема₂. 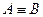тогда и только тогда, когда A«B – тавтология.

Булевы функции.

Переменная х, принимающая значения 0 или 1, называется булевой (или логической, двоичной). Функция F, зависящая от булевых переменных 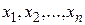и принимающая также значения 0 или 1, называется булевой (или логической, двоичной) и обозначается .

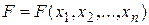Булевы функции F от n переменных могут быть заданы посредством таблицы истинности, содержащей строк и столбцов. В левой части таблицы содержатся наборы значений n переменных, расположенные в порядке возрастания их десятичного эквивалента, а в правой ее части - значения функции F на соответствующих наборах значений переменных.

В качестве примера рассмотрим таблицу истинности некоторой булевой функции F, зависящей от переменных 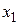, 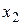и .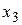

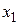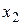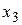			F

Булева функция n переменных F однозначно определяется - разрядным булевым вектором ее значений w(F) (т.е. w(F) - таблица истинности функции F). Например, в этом примере имеем w(F)=(00100111).

Рассматриваемая булева функция F принимает значения 0 на наборах 000, 001, 011 и 100, а значение 1 - на наборах 010, 101, 110 и 111.

Множество наборов, на которых функция F принимает значение 1, называется характеристическим и обозначается через N_F. В настоящем примере имеет место N_F = (010, 101, 110, 111).

Общее число различных булевых функций F от n переменных равно . Т.е. число булевых функций от двух переменных равно , от трех переменных 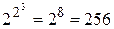.