Задача о переходном процессе в электрической цепи.

Введение.

Мы начинаем изучение одного из основных разделов высшей математики – теории дифференциальных уравнений. Эта теория возникла в конце 17 века одновременно с дифференциальным и интегральным исчислением под влиянием потребностей механики, физики и развивалась в тесной связи с этими науками, а также с техникой. Простейшие дифференциальные уравнения встречались уже в работах И. Ньютона и Г. Лейбница (последний предложил термин «дифференциальные уравнения»). Задача неопределенного интегрирования, т.е. отыскания неизвестной функции по заданной производной – это простейшее дифференциальное уравнение. В трудах Д. Бернулли, Даламбера, Эйлера теория дифференциальных уравнений оформилась в самостоятельную научную дисциплину. Важность этой теории вытекает из того, что основные законы природы, математические закономерности различных процессов выражаются в форме дифференциальных уравнений, а расчет течения этих процессов сводится к отысканию решений этих дифференциальных уравнений. Так обстоит дело в механике (вторая основная задача механики), так обстоит дело и в метеорологии, в теории электроцепей, электродинамике и т.д. В теме «Дифференциальные уравнения» мы рассмотрим основные понятия теории и методы решения простейших дифференциальных уравнений.

Задачи физического характера, приводящие к дифференциальным уравнениям.

Рассмотрим некоторые задачи механики и физики, приводящие к решению обыкновенных дифференциальных уравнений.

Задача о свободном падении тела.

Пусть с некоторой высоты H сброшено тела массы m. Требуется установить, за какое время тело достигнет земной поверхности.

Из условия ясно, что тело движется под действием силы тяжести . Направим ось s отсчета перемещения тела вертикально вниз так, чтобы ее начало совпадало с начальным положением тела. Согласно второму закону Ньютона, имеем

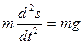, (1)

где m – масса тела, 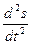- ускорение движущегося тела (вторая производная от перемещения по времени), g – ускорение свободного падения. Уравнение (1) является дифференциальным уравнением второго порядка. Сокращая на m, получим 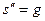. Интегрируя это уравнение, получим

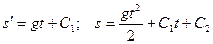(2)

Если в начальный момент времени t=0 скорость и перемещение были соответственно равны s₀ и v₀ , то из уравнений (2) получим v₀ =C_{1 ,} s₀=C₂ . Тогда закон движения тела примет вид

(3)

Подставляя теперь в равенство (3) значения s=H, v₀ =0, s₀ =0, получим формулу для определения времени свободного падения тела: .

Задача о переходном процессе в электрической цепи.

В электрической цепи, содержащей активное сопротивление R, индуктивность L и электродвижущую силу E, в момент времени t=0 замыкается рубильник P. Найти закон, по которому изменяется ток i в данной цепи.

Согласно закону Ома для участка цепи, падение напряжения на активном сопротивлении составит R. При замыкании цепи в катушке L возникает э.д.с. самоиндукции, направленная противоположно току i и пропорциональная производной , причем коэффициент пропорциональности равен L. По второму закону Кирхгофа для RL- цепи при t>0 имеем 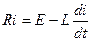, откуда

(4)

Уравнение (4) является линейным дифференциальным уравнением первого порядка с постоянными коэффициентами. Непосредственной подстановкой можно проверить, что общим решением уравнения будет функция

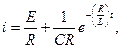(5)

где С – произвольная постоянная. Учитывая, что при t=0 в цепи нет электрического тока (i=0), имеем 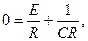откуда 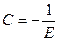. Подставляя значение C в равенство (5), получим закон изменения тока в RL – цепи

(6)

В формуле (6) член 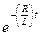убывает с возрастанием t. Таким образом, установившееся значение тока по истечении достаточно большого промежутка времени с момента замыкания RL– цепи определяется величиной 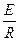. Заметим, что вычисление токов и напряжений в электрических цепях с помощью дифференциальных уравнений является классическим методом расчета цепей в электротехнике.

Понятие общего решения

Дифференциальным уравнением называется уравнение, связывающее независимую переменную 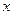, искомую функцию 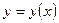и ее производные 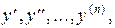то есть уравнение вида

(7)

Если искомая функция 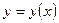есть функция одной независимой переменной x, то дифференциальное уравнение называется обыкновенным.

Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.

Иногда дифференциальное уравнение (7) удается разрешить относительно производной, т.е. привести его к виду

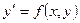(8)

Определение 1. Решением дифференциального уравнения (8) называется дифференцируемая на интервале I функция y=y(x), график которой принадлежит G ( G – открытое множество, в котором 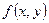определена и непрерывна ) и которая обращает уравнение (8) в тождество.

Определение 2. График решения дифференциального уравнения называется интегральной кривой.

Процесс отыскания решений дифференциальных уравнений называется их решением или интегрированием.

Пример 1. Найти интегральные кривые уравнения

Решение: В каждой точке, отличной от (0,0), угловой коэффициент касательной к искомой интегральной кривой равен 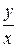, т.е. совпадает с угловым коэффициентом прямой, направленной из начала координат в ту же точку (x,y). Очевидно, что интегральными кривыми в данном случае будут прямые y=cx, так как направление этих прямых всюду совпадает с направлением поля (рис.1).

Общим решением дифференциального уравнения (7) называется функция y= 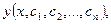зависящая от x и n произвольных постоянных 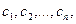обращающих это уравнение в тождество.

Общим решением дифференциального уравнения (8), разрешенного относительно производной, называется непрерывная и имеющая непрерывную частную производную по x функция

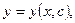(9)

зависящая от одной произвольной постоянной и обращающая это уравнение в тождество.

Частным решением уравнения (8) называется решение, получаемое из общего решения (9) при каком-либо определенном значении произвольной постоянной С.

Определение 3. Соотношение 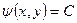называется общим решением или общим интегралом уравнение (8).

Теорема (о существовании общего решения). (без доказательства).

Пусть 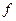и определены и непрерывны на открытом множестве . Тогда для каждой точки можно указать окрестность, в которой существует общее решение уравнения (8).

Рассмотрим частный случай уравнения (8), а именно

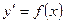(10)

где - заданная непрерывная функция. Как известно, все первообразные для задаются формулой

(11)

Каждая первообразная, определяемая равенством (11) является решением уравнения (10) и по теореме о единственности решения других решений быть не может. В этом случае решение (11), содержащее одну произвольную постоянную C, называется общим решением уравнения (10). Каждое решение, получающееся из общего решения при конкретных значениях произвольной постоянной C, называют частным решением уравнения (10).

Пример 2. Показать, что функция 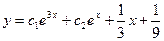является общим решением уравнения .

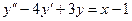Решение. Данная функция содержит две произвольные постоянные, если функция удовлетворяет уравнению, то это и будет означать, что она является общим решением искомого уравнения. Найдем 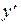и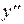

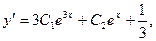
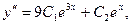
подставляя эти выражения в условия, получаем тождество

Основная задача теории дифференциальных уравнений состоит в отыскании всех решений данного дифференциального уравнения и изучении свойств этих решений. Процесс отыскания решений дифференциального уравнения, названный нами интегрированием дифференциального уравнения, в общем случае весьма трудоемкий и не имеет для большинства типов дифференциальных уравнений конечного алгоритма. Сегодня мы изучим основные свойства дифференциальных уравнений первого порядка и научимся находить общие и частные решения простейших дифференциальных уравнений первого порядка, интегрируемых в квадратурах. Последние слова означают, что решение дифференциального уравнения представлено в конечном виде в аналитической форме. Мы рассмотрим геометрический смысл дифференциального уравнения первого порядка и укажем возможности построения различных алгоритмов приближенного решения дифференциального уравнения на основе этих геометрических рассуждений.