Расчет параметров в характерных точках цикла
Цикл со смешанным подводом теплоты (цикл Тринклера)
Цикл со смешанным подводом теплоты – цикл Тринклера – характерен для так называемых бескомпрессорных двигателей тяжелого топлива.
Особенности: механическое распыление горючего (с помощью плунжерного насоса), внутреннее смесеобразование, самовоспламенение от сжатого до высокой температуры воздуха.
Это теоретический цикл всех современных транспортных и стационарных дизелей.
Изобразим цикл на рабочей и тепловой диаграмме (рис.3).

Рис.3. Цикл Тринклера. Рабочая (p-v) и тепловая (T-s) диаграммы.
Рассмотрим термодинамические процессы цикла:
1-2 – адиабатное сжатие,
2-3 – изохорный подвод теплоты,
3-4 – изобарный подвод теплоты,
4-5 – адиабатное расширение,
5-1 – изохорный отвод теплоты.
Характеристики цикла:
 - степень сжатия (отношение объемов в начале и конце процесса сжатия 1-2).
- степень сжатия (отношение объемов в начале и конце процесса сжатия 1-2).
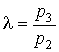 - степень повышения давления (отношение давлений в процессе изохорного подвода теплоты).
- степень повышения давления (отношение давлений в процессе изохорного подвода теплоты).
 - степень предварительного расширения (отношение объемов в процессе изобарного подвода теплоты).
- степень предварительного расширения (отношение объемов в процессе изобарного подвода теплоты).
При анализе считают известными: состояние рабочего тела в т.1( Т1, p1) и характеристики цикла ε, λ, ρ. Вместо одной из характеристик может быть задана максимальная температура или максимальное давление.
Расчет цикла заключается в определении:
· параметров состояния рабочего тела в характерных точках цикла (p, T, v),
· энергетических характеристик цикла: подводимой удельной теплоты q1, отводимой удельной теплоты q2, цикловой работы lц и термического КПД цикла ηt .
Расчет параметров в характерных точках цикла
Для определения параметров состояния в точке 2 рассмотрим процесс 1-2 - адиабатное сжатие. Запишем уравнение адиабатного процесса в следующем виде:
pv k = const, или  .
.
Выразим из уравнения давление в т.2:
 .
.
Для определения температуры в т.2 запишем уравнение адиабатного процесса в виде:
Tvk-1=const, или T1v1k-1=T2v2k-1.
Отсюда:
 .
.
Для определения параметров состояния в точке 3 рассмотрим процесс 2-3 - изохорный процесс с подводом теплоты, при этом давление возрастает пропорционально температуре:
 .
.
Давление в т.3 можно рассчитать по формуле:
 .
.
Температура в т.3:
 .
.
Для определения параметров состояния в точке 4 рассмотрим процесс 3-4 – изобарное расширение с подводом теплоты, при этом удельный объем возрастает пропорционально температуре:
 .
.
Давление в т.4: р4=р3.
Температура в т.4:
 .
.
Определим параметры состояния в точке 5.
Рассмотрим процесс 4-5 - адиабатное расширение. Используя уравнение адиабатного процесса, получим выражение для абсолютного давления в т.5:

Для определения абсолютной температуры в т.5 рассмотрим изохорной процесс 5-1.
Для изохорного процесса:
 .
.
Отсюда:
 .
.
Определив таким образом давление и температуру в характерных точках,можно рассчитать удельный объем v в каждой точке, используя уравнение Клапейрона.
 .
.
