Приближенное решение определенных интегралов
В тех случаях, когда при вычислении определенного интеграла невозможно найти первообразную или она очень сложна для вычислений, используют формулы приближенного вычисления.
Геометрический смысл определенного интеграла 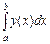 – площадь криволинейной трапеции, ограниченной осью
– площадь криволинейной трапеции, ограниченной осью 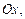 кривой
кривой 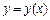 и прямыми
и прямыми 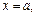
 Разобьем отрезок
Разобьем отрезок  на
на 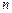 равных частей точками
равных частей точками 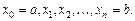 Получим
Получим 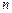 элементарных криволинейных трапеций.
элементарных криволинейных трапеций.
Формулы прямоугольников.Площадь каждой элементарной трапеции можно приближенно вычислить как площадь прямоугольника.
Если построить прямоугольник, используя левую границу элементарной трапеции, получим формулу левых прямоугольников:
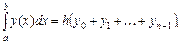
где 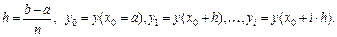
Очевидно, что чем больше  тем точнее будет найдено значение интеграла.
тем точнее будет найдено значение интеграла.
Если построить прямоугольник, используя правую границу элементарной трапеции, получим формулу правых прямоугольников:
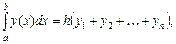
где 
Для повышения точности вычисления можно построить прямоугольник, со стороной, равной значению подынтегральный функции в середине элементарного отрезка, получим формулу центральных прямоугольников:
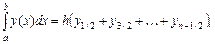
где 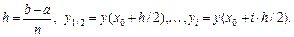
На практике при вычислении определенного интеграла численными методами часто требуется обеспечить точность вычисления 
Для оценки точности выполняют два расчета с числом разбиений 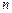 и
и  Вычисления заканчиваются, если
Вычисления заканчиваются, если  при невыполнении неравенства число разбиений удваивается и вновь производится сравнение результатов.
при невыполнении неравенства число разбиений удваивается и вновь производится сравнение результатов.
Пример 1: Вычислить определенный интеграл 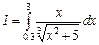 используя формулы левых, правых и центральных прямоугольников. Обеспечить точность вычисления
используя формулы левых, правых и центральных прямоугольников. Обеспечить точность вычисления 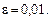
Вводим отрезок интегрирования  (рис. 28),
(рис. 28), 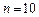 (С2),
(С2),  (D2). Вычисляем значения подынтегральной функции на концах отрезка (B4, C4).
(D2). Вычисляем значения подынтегральной функции на концах отрезка (B4, C4).
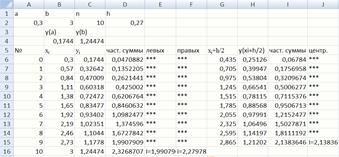
Рис. 28. Численное интегрирование по формулам прямоугольников
Заполнить блок А6:С16 самостоятельно.
Для заполнения ячейки D6используется формула =$D$2*C6. Для заполнения ячейки D7используется формула =$D$2*C7+D6, далее она протягивается вниз и заполняем весь столбец D.
Для заполнения ячейки Е6используется формула (рис. 29).
Для заполнения ячейки F6используется формула (рис. 30).

Рис. 29. Формула для заполнения ячейки Е6
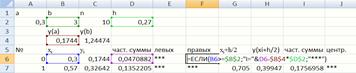
Рис. 30. Формула для заполнения ячейки F6
Далее они протягиваются вниз и заполняют столбцы EиF.
Заполнить блок G6:I15 самостоятельно.
Для заполнения ячейки J6используется формула (рис. 31).Далее она протягивается вниз и заполняет столбец J.

Рис. 31. Формула для заполнения ячейки J6
Выполняем вычисление определенного интеграла для 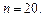
Оценку точности рассмотрим на примере формулы центральных прямоугольников.

Формула трапеций. Площадь каждой элементарной криволинейной трапеции можно приближенно вычислить как площадь трапеции, получим формулу трапеций:
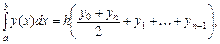
где 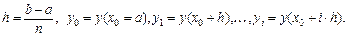
Очевидно, что чем больше  тем точнее будет найдено значение интеграла.
тем точнее будет найдено значение интеграла.
Пример 2: Вычислить определенный интеграл 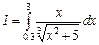 используя формулу трапеций. Обеспечить точность вычисления
используя формулу трапеций. Обеспечить точность вычисления 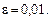
Вводим отрезок интегрирования  (рис. 32),
(рис. 32), 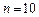 (С2),
(С2),  (D2). Вычисляем значения подынтегральной функции на концах отрезка (B4, C4).
(D2). Вычисляем значения подынтегральной функции на концах отрезка (B4, C4).
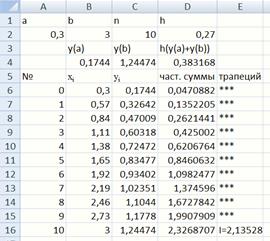
Рис. 32. Численное интегрирование по формуле трапеций
Заполнить ячейку D4 и блокА6:C16 самостоятельно.
Для заполнения ячейки D6используется формула =$D$2*C6. Для заполнения ячейки D7используется формула =$D$2*C7+D6, далее она протягивается вниз и заполняем весь столбец D.
Для заполнения ячейки Е6используется формула (рис. 33).Далее она протягивается вниз и заполняет весь столбец E.

Рис. 33. Формула для заполнения ячейки E6
Выполняем вычисление определенного интеграла для 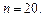

Формула Симпсона. Разобьем отрезок интегрирования  на четное число элементарных отрезков точками
на четное число элементарных отрезков точками 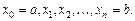
Подынтегральная функция на каждом элементарном отрезке двойной длины заменяется параболой. Значение интеграла приближенно вычисляется по формуле Симпсона:
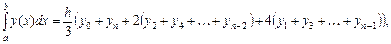
где 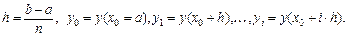
Очевидно, что чем больше  тем точнее будет найдено значение интеграла.
тем точнее будет найдено значение интеграла.
Пример3: Вычислить определенный интеграл 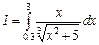 используя формулу Симпсона. Обеспечить точность вычисления
используя формулу Симпсона. Обеспечить точность вычисления 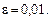
Вводим отрезок интегрирования  ,
, 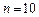 (С2), заполняем ячейку D2(рис. 33). Вычисляем значения подынтегральной функции на конце отрезка (C4).
(С2), заполняем ячейку D2(рис. 33). Вычисляем значения подынтегральной функции на конце отрезка (C4).

Рис. 33. Формула для заполнения ячейки E6
Заполнить блокА6:C16 самостоятельно.
Для заполнения ячейки D6используется формула =C6. Для заполнения ячейки D7используется формула =ЕСЛИ(ОСТАТ(A7;2)=0;D6+2*C7;D6+4*C7), далее она протягивается вниз и заполняем весь столбец D(рис. 34).
Для заполнения ячейки Е6используется формула (рис. 35).Далее она протягивается вниз и заполняет весь столбец E.
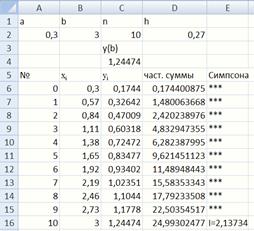
Рис. 34. Численное интегрирование по формуле Симпсона

Рис. 35. Формула для заполнения ячейки E6
Выполняем вычисление определенного интеграла для 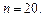

Задания для самостоятельного выполнения.
Из таблицы 5 приложения взять исходные данные своего варианта. Вариант определяется по порядковому номеру в списке группы. Выполнить численное интегрирование по формулам прямоугольников, трапеций и Симпсона. Обеспечить точность вычисления 
Контрольные вопросы
1. Формулы прямоугольников.
2. Погрешность формул численного интегрирования
3. Формула трапеций.
4. Формула Симпсона.
