Необходимый признак сходимости

Если ряд сходится, то его общий член u_n­ стремится к нулю при n → ∞, т.е. .

Указанный признак не является достаточным, т.е. если u_n → 0, то о сходимости ряда ничего сказать нельзя.

Достаточные признаки

Признак сравнения

Если даны два ряда

и с положительными членами, причем члены первого ряда не превосходят соответствующих членов второго ряда: 0 ≤ u_n ≤ v_n , то

а) из сходимости второго ряда следует сходимость первого ряда;

б) из расходимости первого ряда следует расходимость второго ряда.

Для сравнения часто используются ряды:

Ряд геометрической прогрессии:

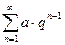
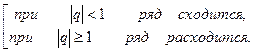
Обобщенно-гармонический ряд:

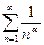
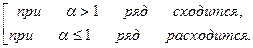
Предельный признак сравнения

Если даны два ряда

и с положительными членами и существует конечный предел , то рассматриваемые ряды одновременно сходятся или расходятся.

Признак Даламбера

Если ряд с положительными членами таков, что существует предел

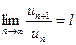, то

Радикальный признак Коши

Если ряд с положительными членами таков, что существует предел

, то

Интегральный признак Коши

Если функция f(x) непрерывная, положительная и невозрастающая для x ≥ a и, начиная с некоторого n= N,

u_n = f(n), то ряд и несобственный интеграл одновременно сходятся или расходятся.

Признак Лейбница о сходимости знакочередующихся рядов

Ряд u₁ – u₂ + u₃ - … + (-1)ⁿ⁺¹ u_n + …, где все u_n > 0, называется знакочередующимися.

Если члены знакочередующегося ряда удовлетворяют условиям

u₁ > u₂ > u₃ > … > u_n , и 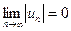, то такой ряд сходится.

Если ряд сходится, а ряд 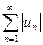расходится, то такой ряд называют условно сходящимся.

Если ряд 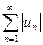сходится, то сходится и ряд , который в этом случае называют абсолютно сходящимся.

Степенные ряды

Степенным рядом называется ряд вида

,

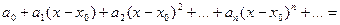
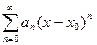где a_n – числа, коэффициенты степенного ряда.

При х₀ = 0 степенной ряд имеет вид:

.

Значения х, при которых степенной ряд является сходящимся числовым рядом, образуют область сходимости ряда.

Об области сходимости степенного ряда можно судить, исходя из теоремы:

Если степенной ряд сходится при х = х₀ ≠ 0, то он абсолютно сходится при всех значениях х, удовлетворяющих неравенству |x| < |x₀|.

Число R называется радиусом сходимости степенного ряда, его находят по формуле: .

Пример выполнения задания 1

Исследуем на сходимость числовые ряды.

а) .

Общий член ряда 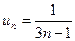и 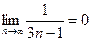. Сравним данный ряд с гармоническим рядом являющимся расходящимся. Так как 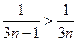, то исходный ряд по признаку сравнения расходится.

б) +… .

Общий член ряда 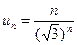и его предел

.

Применим правило Лопиталя: .

Необходимый признак сходимости выполняется.

Воспользуемся признаком Даламбера:

; ,

.

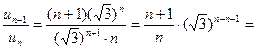
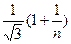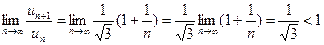Следовательно, ряд сходится.

в) .

Это знакочередующийся ряд с общим членом .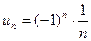

Воспользуемся признаком Лейбница:

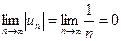и .

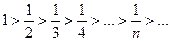Следовательно, ряд сходится.

Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:

.

Это гармонический ряд. Он расходится. Значит, данный ряд сходится условно.

Пример выполнения задания 2

Определить радиус и область сходимости степенного ряда

.

Решение.

Обозначим х + 1 = Х и рассмотрим ряд

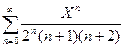. Определим его радиус сходимости

, ,

.

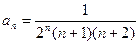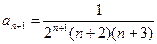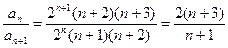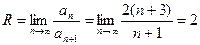, значит, для всех |Х| < 2 ряд сходится.

Решением неравенства является интервал (-2,2).

Рассмотрим поведение ряда на концах полученного интервала

При Х = -2 имеем

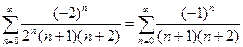- ряд знакочередующийся.

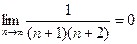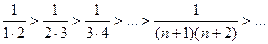и Следовательно, по признаку Лейбница ряд сходится.

При Х = 2 имеем:

.

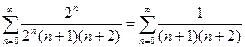Сравним его с обобщенно-гармоническим рядом .

Он является сходящимся.

Так как 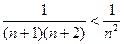, то данный ряд сходится.

Степенной ряд сходится на обоих концах интервала сходимости.

-2 ≤ Х ≤ 2 ,

-2 ≤ x + 1 ≤ 2,

-3 ≤ x ≤ 1.

Таким образом, областью сходимости данного ряда является интервал вида х [-3;1].

Сведения из теории

Ряды Фурье

Пусть f(x) – какая-нибудь функция с периодом 2π. Рядом Фурье функции f(x) называется тригонометрический ряд

, коэффициенты которого определяются по формулам Фурье:

; , n = 1,2,3,…;

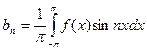, n = 1,2,3,….

Из этого определения не следует, что f(x) всегда разлагается в свой ряд Фурье.

Функция f(x) удовлетворяет условиям Дирихле на отрезке

[-π; π], если:

1) она имеет конечное число экстремумов на [-π; π];

2) она на этом отрезке непрерывна, за исключением конечного числа точек разрыва 1-го рода;

3) существуют конечные предельные значения функции

f(-π + 0) и f(π - 0).

Теорема Дирихле: если функция f(x) на отрезке [-π; π] удовлетворяет условиям Дирихле, то ряд Фурье функции f(x) сходится для всех х, а его сумма равна значению f(x) в каждой точке непрерывности этой функции, и равна числу в каждой точке разрыва.

Если функция f(x) задана на отрезке [-l;l], где l – произвольное число, причём f(x + 2l) = f(x), и она удовлетворяет условиям Дирихле, то функция может быть разложена в ряд Фурье:

, где

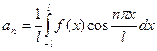; , n = 1,2,3,…;

, n = 1,2,3,….

Если функция f(x) чётная, т.е. f(-x) = f(x), то ,

;

; .

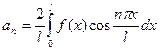Если функция f(x) нечётная, т.е. f(-x) = -f(x), то ,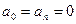

;

.

Пример выполнения задания 3

Разложим в ряд Фурье функцию f(x) периода 2π, заданную на отрезке [-π; π] формулой

Эта функция удовлетворяет условиям Дирихле, значит, её можно разложить в ряд Фурье. Находим коэффициенты ряда:

;

,

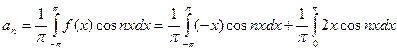интегрируя по частям, получим:

= .

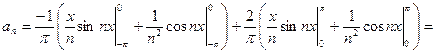
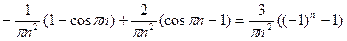Аналогично находим

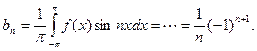
Исходной функции f(x) соответствует ряд Фурье

f(x)= .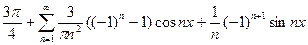

IV семестр

Вопросы

1. Непрерывное преобразование Лапласа. Оригинал и

изображение.

1. Таблица оригиналов и изображений.
2. Свойства преобразования Лапласа.
3. Дифференцирование и интегрирование оригинала.
4. Дифференцирование и интегрирование изображения.
5. Метод операционного исчисления при решении дифференциальных уравнений и их систем.
6. Случайные события. Классификация событий.
7. Вероятность события. Основные определения вероятности события.
8. Сумма и произведение событий.
9. Условная вероятность
10. Теоремы сложения вероятностей.
11. Формула полной вероятности.
12. Формула Байеса.
13. Последовательность независимых испытаний. Формула Бернулли.
14. Формула Пуассона.
15. Формула Муавра-Лапласа.
16. Дискретные и непрерывные случайные величины. Закон распределения.
17. Функция распределения. Её свойства.
18. Числовые характеристики дискретной случайной величины. Их свойства.
19. Числовые характеристики непрерывной случайной величины. Их свойства.
20. Биноминальное распределение.
21. Пуассоновское распределение.
22. Равномерное распределение.
23. Показательное распределение.
24. Нормальное распределение.
25. Вероятность попадания случайной величины на заданный участок.

Модуль 9

Операционное исчисление

Задачи для решения

Задание 1

Пользуясь преобразованием Лапласа и основными его свойствами, найти изображения функций:

1. ;

2. ;

3. ;

4. ;

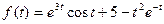5. ;

6. ;

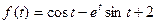7. ;

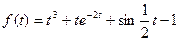8. ;

9. ;

10. .

Задание 2

По известному изображению F(p) найти оригинал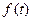

1. ;

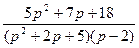2. ;

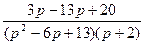3. ;

4. ;

5. ;

6. ;

7. ;

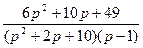8. ;

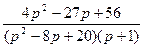9. ;

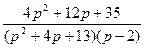10. ;

Задание 3

Методами операционного исчисления найти решение дифференциального уравнения, удовлетворяющее начальным условиям.

1.

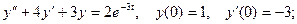
2.

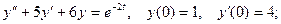
3.

4.

5.

6.

7.

8.

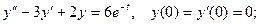
9.

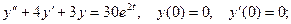
10.

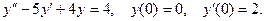
Задание 4.

Решить систему дифференциальных уравнений при заданных начальных условиях.

1.

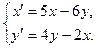
2.

3. .

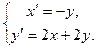
4.

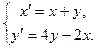
5.

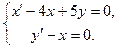
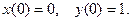
6.

7.

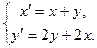
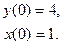
8.

9.

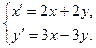
10. .

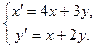
Решение типовых задач

Задание 1

Пользуясь преобразованием Лапласа и основными его свойствами, найти изображения функции

.

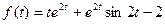Задание 2

По известному изображению F(p) найти оригинал .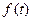

.

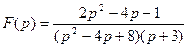Задание 3

Методами операционного исчисления найти решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.

.

Задание 4

Решить систему дифференциальных уравнений при заданных начальных условиях.

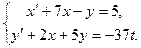
Начальные условия: .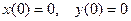

Сведения из теории

Функцией – оригиналом называют функцию 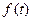действительного аргумента 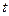, удовлетворяющую условиям:

1. для всех отрицательных значений аргумента функция тождественно равна нулю, т.е.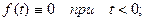

2. функция 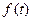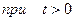возрастает не быстрее показательной функции, т.е. существуют такие постоянные ;

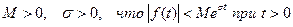3. на любом конечном отрезке положительной полуоси 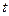эта функция удовлетворяет условиям Дирихле:

- ограничена;

- непрерывна или имеет конечное число точек разрыва

первого рода;

- имеет конечное число экстремумов.

Изображением функции 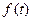по Лапласу (преобразованием по Лапласу ) называют функцию комплексной переменной определяемую соотношением .

Интеграл в правой части называется интегралом Лапласа.

Функция определяется в полуплоскости и является в этой области аналитической функцией.

Функция комплексной переменной является изображением по Лапласу функции действительного аргумента 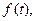обозначатся

или .
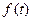