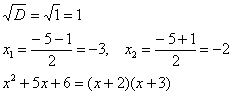Интегрирование дробно-рациональной функции. Метод неопределенных коэффициентов

Продолжаем заниматься интегрированием дробей. Интегралы от некоторых видом дробей мы уже рассмотрели на уроке Интегрирование некоторых дробей, и этот урок в некотором смысле можно считать продолжением. Для успешного понимания материала необходимы базовые навыки интегрирования, поэтому если Вы только приступили к изучению интегралов, то есть, являетесь чайником, то необходимо начать со статьи Неопределенный интеграл. Примеры решений.

Как ни странно, сейчас мы будем заниматься не столько нахождением интегралов, сколько… решением систем линейных уравнений. А именно – нужно хорошо ориентироваться в методах подстановки («школьном» методе) и методе почленного сложения (вычитания) уравнений системы линейных алгебраических уравнений.

Что такое дробно-рациональная функция? Простыми словами, дробно-рациональная функция – это дробь, в числителе и знаменателе которой находятся многочлены либо произведения многочленов. При этом дроби являются более навороченными, нежели те, о которых шла речь в статье Интегрирование некоторых дробей.

Интегрирование правильной дробно-рациональной функции

Сразу пример и типовой алгоритм решения интеграла от дробно-рациональной функции.

Пример 1

Найти неопределенный интеграл

.

Шаг 1.Первое, что мы ВСЕГДА делаем при решении интеграла от дробно-рациональной функции – это выясняем следующий вопрос: является ли дробь правильной?Данный шаг выполняется устно, и вот как:

Сначала смотрим на числитель и выясняем старшую степень многочлена:

.

Старшая степень числителя равна двум.

Теперь смотрим на знаменатель и выясняем старшую степень знаменателя. Напрашивающийся путь – это раскрыть скобки и привести подобные слагаемые, но можно поступить проще, в каждойскобке находим старшую степень

и мысленно умножаем: – таким образом, старшая степень знаменателя равна трём. Совершенно очевидно, что если реально раскрыть скобки, то мы не получим степени больше трёх.

Вывод:Старшая степень числителя СТРОГОменьше старшей степени знаменателя, значит, дробь является правильной.

Если бы в данном примере в числителе находился многочлен 3, 4, 5 и т.д. степени, то дробь была бы неправильной.

Сейчас мы будем рассматривать только правильные дробно-рациональные функции. Случай, когда степень числителя больше либо равна степени знаменателя, разберём в конце урока.

Шаг 2. Разложим знаменатель на множители. Смотрим на наш знаменатель:

.

Вообще говоря, здесь уже есть произведение множителей, но, тем не менее, задаемся вопросом: нельзя ли что-нибудь разложить еще? Объектом пыток, несомненно, выступит квадратный трехчлен. Решаем квадратное уравнение, ищем его корни:

Дискриминант уравнения больше нуля, значит, трехчлен действительно раскладывается на множители.