Показательным называют распределение вероятностей по формуле

где - плотность потока, или среднее число событий за единицу времени.

Примером непрерывной случайной величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока.

Пусть T – время безотказной работы некоторого прибора. Эта случайная величина имеет показательное распределение, интегральная функция которого

Здесь - вероятность того, что за время длительностью прибор хотя бы раз откажет.

Тогда - вероятность безотказной работы прибора за то же время.

Функцией надежности называем . Заметим, что .

Задача

Испытываются 100 приборов, работающих независимо друг от друга. Длительность времени безотказной работы каждого распределена по показательному закону

.

Найти вероятность того, что в интервале времени не откажет большинство приборов.

Р е ш е н и е

.

Найдем вероятность того, что за время длительностью один (любой) прибор не откажет. Функция надежности .

.

Далее нас интересует вероятность того, что из 100 приборов за время число работающих будет от 50 до 100. Мы находимся в условиях интегральной теоремы Муавра-Лапласа:

;

;

;

;

;

.

Событие с такой вероятностью можно считать практически достоверным.

Равномерное распределение

[1], Гл. XI, § 6

Пусть значения случайной величины 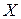составляют интервал . Пусть вероятность того, что случайная величина попадет в интервал , полностью принадлежащей интервалу , зависит только от его длины и не зависит от его положения на оси. Мы имеем случайную величину с распределением, которое называется равномерным и задается дифференциальной функцией вида:

Математическое ожидание совпадает с абсциссой середины интервала и равно:

.

Дисперсия равномерно распределенной случайной величины равна

.

Задача

Поезда метрополитена идут с интервалом 2 мин. Время T, в течение которого пассажиру приходится ждать поезда, подчиняется равномерному распределению.

Найти вероятность того, что пассажир, пришедший на станцию, будет ждать поезд не более 1 мин.

Р е ш е н и е

Запишем дифференциальную функцию случайной величины T:

Тогда .

Случайные векторы

Двумерной дискретной случайной величиной (или случайным вектором), обозначаемой символом , называется система из двух одномерных дискретных случайных величин x и h, определенных на одном и том же вероятностном пространстве .

Ряд распределения случайного вектора определяется как множество всех упорядоченных тpоек вида , где – возможные значения случайной величины , – возможные значения случайной величины , а .

Введем следующие обозначения: , , , и . Тогда получаем , , и

Отсюда, учитывая свойства ряда распределения случайной величины x, имеем

Пример.Подбрасывают две игральные кости. Случайная величина – число выпадений «шестерки», а случайная величина – число выпадений нечетной цифры. Для описания ряда распределения случайного вектора необходимо определить множество всех возможных пар значений . Множество для этого эксперимента состоит из равновероятных исходов вида . Число элементов этого множества . Данный эксперимент можно рассматривать как повторение двух независимых испытаний с одним и тем же множеством исходов в каждом опыте . Поэтому , что соответствует приведенной выше записи. Каждая из указанных случайных величин может принимать значения из множества . Найдем сначала законы распределения компонент.

Событие соответствует числу успехов в серии из двух независимых испытаний. Вероятность этого события равна вероятности получить ровно успехов в двух опытах по схеме Бернулли с вероятностью успеха в одном опыте . По формуле Бернулли получаем

.

Значит случайная величина имеет ряд распределения

Аналогично, используя соответствующую схему Бернулли для вычисления вероятностей событий , получим

Заметим, что , ибо это вероятности невозможных событий. Далее, событие состоит в том, что дважды выпала или «двойка», или «четверка». Вероятность выпадения или «двойки», или «четверки» в одном эксперименте равна . По формуле Бернулли

.

Теперь воспользуемся тем, что , т. е., . Откуда . Аналогично получаем , что , то есть, . Откуда . Точно таким же образом находим и . Наконец, из равенства находим . Теперь можно записать ряд распределения случайного вектора , представляя его в виде таблицы.

Продолжая исследования случайного вектора , найдем условную вероятность:

Аналогично:

Покажем, что для условных вероятностей справедливы равенства:

Действительно, согласно определению, получаем

Пример.Известен ряд распределения случайного вектора (x,h)

x \ h	-1
-2	1/16	1/16
-1	1/48	1/48
	1/24	1/8
	2/8	1/48
	1/48	3/8

Построить ряд распределения случайного вектора с компонентами х = x+h и у = xh.

Р е ш е н и е

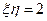Легко проверяется, что x+h и xh . Далее имеем и, следовательно, , причем .

Для имеем , причем .

Для имеем , причем и , причем .

Для имеем , причем .

Для имеем или , причем и .

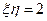Для имеем , причем . И наконец для имеем , причем .

Таким образом, получаем ряд распределения случайного вектора

X \ Y	-2	-1
-3					1/16	1/16
-2				1/48		1/48
-1	1/16		1/24			5/48
		13/48				13/48
	1/48		1/8			7/48
				1/48		1/48
					3/8	3/8
	1/12	13/48	1/6	1/24	7/16

Индивидуальные задания.

Варианты заданий

Задание 1.

1. Из урны, содержащей 4 белых и 4 черных шара, наугад извлекают три шара. Пусть X – число вынутых черных шаров. Построить ряд распределения случайной величины X. Вычислить математическое ожидание и дисперсию, а также построить функцию распределения.
2. Имеется 5 одинаковых урн, расположенных в ряд и содержащих каждая по 4 шара белого или черного цвета, причем в k-ой по порядку урне содержится ровно (k-1) белый шар. Наугад выбирается урна и из нее извлекают два шара, оказавшихся белыми. Какова вероятность извлечь еще один белый шар из этой же урны?
3. Известен ряд распределения случайного вектора (x,h)

x \ h	-1
-2	1/16	1/16
-1	1/48	1/48
	1/24	1/8
	2/8	1/48
	1/48	3/8

Найти D(x+h).

Задание 2.

1. Охотник, имеющий 5 патронов, стреляет в цель до первого попадания или пока не израсходует все патроны. Вероятность попадания при каждом выстреле равна 0,8. Составить закон распределения случайной величины X, представляющей число израсходованных патронов. Вычислить математическое ожидание и дисперсию, а также построить функцию распределения.
2. На шахматную доску ставят наудачу двух слонов, белого и черного Какова вероятность того, что слоны побьют друг друга?
3. Известен ряд распределения случайного вектора (x,h)

x \ h	-1
-2	1/16	1/16
-1	1/48	1/48
	1/24	1/8
	2/8	1/48
	1/48	3/8

Построить ряд распределения случайного вектора с компонентами х = x+h и у = xh.

Задание 3.

1. Из ящика, содержащего 3 бракованных и 6 годных деталей, наугад извлекают 5. Пусть X – число вынутых годных деталей. Построить ряд распределения случайной величины X. Вычислить математическое ожидание и дисперсию, а также построить функцию распределения.
2. Две игральные кости бросают до выпадения «6» хотя бы на одной из них. Найти вероятность того, что впервые это произойдет при четвертом бросании.
3. Известен ряд распределения случайного вектора (x,h)

x \ h	-1
-2	1/16	1/16
-1	1/48	1/48
	1/24	1/8
	2/8	1/48
	1/48	3/8

Построить ряд распределения случайного вектора с компонентами х = x+h и у = x-h.

Задание 4.

1. Из каждой партии телевизоров для контроля извлекают 4 и последовательно их проверяют. При появлении плохо работающего телевизора бракуется вся партия. Пусть X – количество проверенных телевизоров до появления бракованного, и вероятность брака равна 0,2. Составить закон распределения случайной величины X. Вычислить математическое ожидание и дисперсию, а также построить функцию распределения.
2. Вероятность успеха в каждом испытании Бернулли равна р. Найти вероятность того, что в серии из 10 испытаний третий по порядку успех наступит при пятом испытании.
3. Известен ряд распределения случайного вектора (x,h)

x \ h	-1
-2	1/16	1/16
-1	1/48	1/48
	1/24
	3/8	1/24
		3/8

Построить ряд распределения случайного вектора с компонентами х = x+h и у = x.

Задание 5.

1. В колоде осталось 7 карт, из них 3 козырных. Наугад выбирают 4 карты. Пусть X – число взятых козырных карт. Построить ряд распределения случайной величины X. Вычислить математическое ожидание и дисперсию, а также построить функцию распределения.
2. Из урны, содержащей 3 белых, 4 черных и 2 красных шара, последовательно, без возвращения извлекают по одному шару до появления красного шара. Найти вероятность того, что были извлечены 2 белых и 1 черный шар.
3. Известен ряд распределения случайного вектора (x,h)

x \ h	-1
-2	1/16	1/16
-1	1/48	1/48
	1/24
	3/8	1/24
		3/8

Построить ряд распределения случайного вектора с компонентами х = x+h и у = x-h.

Задание 6.

1. Имеется 5 различных ключей, из которых только один подходит к замку. Составить закон распределения числа опробованных ключей при открывании замка, если испробованный ключ в последующих попытках открыть замок не используется. Вычислить математическое ожидание и дисперсию, а также построить функцию распределения.
2. Из урны, содержащей 3 белых, 4 черных и 2 красных шара, последовательно, без возвращения извлекают по одному шару до появления красного шара. Найти вероятность того, что не появилось ни одного белого шара.
3. Известен ряд распределения случайного вектора (x,h)

x \ h	-1
-2	1/16	1/16
-1	1/48	1/48
	1/24
	3/8	1/24
		3/8

Построить ряд распределения случайного вектора с компонентами х = x+h и у = xh.

Задание 7.

1. В цехе имеется 5 однотипных станков. Вероятность выхода из строя одного станка равна 0,8. Пусть случайная величина X равна количеству станков, потребовавших ремонта. Составить закон распределения этой случайной величины. Вычислить математическое ожидание и дисперсию, а также построить функцию распределения.
2. Из урны, содержащей 3 белых, 4 черных и 2 красных шара, последовательно, без возвращения извлекают по одному шару до появления красного шара. Найти вероятность того, что всего было извлечено три шара.
3. Известен ряд распределения случайного вектора (x,h)

x \ h	-1
-2	1/16	1/16
-1	1/48	1/48
	1/24
	3/8	1/24
		3/8

Найти D(x+h).

Задание 8.

1. Имеется 9 радиоламп, среди которых 3 неисправных. Наугад берутся 4 радиолампы и проверяются на годность. Построить ряд распределения неисправных радиоламп. Вычислить математическое ожидание и дисперсию, а также построить функцию распределения.
2. Из урны, содержащей 4 белых и 3 черных шара последовательно извлекают все шары. Найти вероятность того, что вторым будет извлечен белый шар, а третьим – черный.
3. Известен ряд распределения случайного вектора (x,h)

x \ h	-1
-2	1/16	1/16
-1	1/48	1/48
	1/24
	3/8	1/24
		3/8

Найти D(x+h).

Задание 9.

1. Производится тестирование 5 больших интегральных схем (БИС). Вероятность того, что БИС неисправна, равна 0,6. Построить ряд распределения случайной величины X, представляющей собой количество неисправных БИС. Вычислить математическое ожидание и дисперсию, а также построить функцию распределения.
2. Имеется 5 одинаковых урн, расположенных в ряд и содержащих каждая по 4 шара белого или черного цвета, причем в k-ой по порядку урне содержится ровно (k-1) белый шар. Наугад выбирается урна и из нее извлекают два шара, оказавшихся белыми. Какова вероятность того, что эти шары извлечены из третьей урны?
3. Известен ряд распределения случайного вектора (x,h)

x \ h	-1
-2	1/16	1/16
-1	1/48	1/48
	1/24
	3/8	1/24
		3/8

Найти D(x-h).

Задание 10.

1. Пусть случайная величина X – количество гербов, полученных при бросании 4 монет. Составить закон распределения этой случайной величины. Вычислить математическое ожидание и дисперсию, а также построить функцию распределения.
2. В ящике 12 шаров, из них 5 синих и 7 красных. Шар вынимают наугад. Проводится 6 таких испытаний. Какова вероятность того, что будет извлечено 3 синих шара?
3. Известен ряд распределения случайного вектора (x,h)

x \ h	-1
-2	1/16	1/16
-1	1/48	1/48
	1/24
	3/8	1/24
		3/8

Найти D(x-h).

Задание 11.

1. В ящике содержится 7 стандартных и 3 бракованных детали. Детали извлекают последовательно до появления стандартной, не возвращая их обратно. Какова вероятность того, что будет произведено 2 извлечения?
2. При бросании 2 игральных костей игрок выигрывает 25 руб., если на обеих костях выпадает по 6 очков, 3 руб. – если на одной из костей выпало 6 очков, 1 руб. – если сумма выпавших очков равна 6. Пусть случайная величина X равна выигрышу, возможному при одном бросании. Составить закон распределения этой случайной величины. Вычислить математическое ожидание и дисперсию, а также построить функцию распределения.
3. Известен ряд распределения случайного вектора (x,h)

x \ h	-1
-2	1/16	1/16
-1	1/48	1/48
	1/24
	3/8	1/24
		3/8

Найти D(x+h).

Задание 12.

1. В первой урне 3 белых и 5 черных шаров, во второй – 6 белых и 4 черных шара, в третьей – 1 белый и 3 черных шара. Из каждой урны вынимают по 1 шару. Пусть случайная величина X – количество извлеченных черных шаров. Составить закон распределения этой случайной величины. Вычислить математическое ожидание и дисперсию, а также построить функцию распределения.
2. По мишени ведутся выстрелы до первого попадания или до израсходования всех 5 патронов. Найти вероятность того, что будет произведено 5 выстрелов.
3. Известен ряд распределения случайного вектора (x,h)

x \ h	-1
-1	1/16		1/16
	1/48	1/24	1/48
		3/8
	3/8		1/24

Найти D(x-h).

Задание 13.

1. В группе из 5 изделий имеется 1 бракованное. Чтобы его обнаружить, наугад берут одно изделие за другим и проверяют. Построить ряд распределения случайной величины X, представляющей собой количество взятых изделий до обнаружения бракованного. Вычислить математическое ожидание и дисперсию, а также построить функцию распределения.

2. Существуют ли такие события и , что и ?

1. Известен ряд распределения случайного вектора (x,h)

x \ h	-1
-1	1/16		1/16
	1/48	1/24	1/48
		3/8
	3/8		1/24

Найти D(x+h).

Задание 14.

1. В партии, состоящей из 10 деталей, имеется 4 бракованных. Наугад извлекают 3 детали. Составить закон распределения случайной величины X, представляющей собой количество бракованных деталей среди 3 выбранных. Вычислить математическое ожидание и дисперсию, а также построить функцию распределения.

2. Пусть события и таковы, что и . Показать, что события и независимы.

1. Известен ряд распределения случайного вектора (x,h)

x \ h
-1	1/16		1/16
	1/48	1/24	1/48
		3/8
	3/8		1/24

Построить ряд распределения случайного вектора с компонентами х = xh и у = x-h.

Задание 15.

1. В лотерее разыгрывается мяч стоимостью 4 руб. и шахматы стоимостью 10 руб. Всего 10 билетов. Пусть случайная величина X представляет собой величину выигрыша в рублях для лица, имеющего 3 билета. Составить закон распределения этой случайной величины. Вычислить математическое ожидание и дисперсию, а также построить функцию распределения.
2. Монету сто раз бросили и сто раз выпал герб. Какова вероятность, что и в сто первый раз выпадет герб?
3. Известен ряд распределения случайного вектора (x,h)

x \ h
-1	1/16		1/16
	1/48	1/24	1/48
		3/8
	3/8		1/24

Построить ряд распределения вектора с компонентами х = x+h и у = x-h..

Задание 16.

1. Из урны, содержащей 4 белых и 4 черных шара последовательно извлекают шары до появления первого белого, не возвращая их обратно в урну. Составить закон распределения случайной величины X – числа извлеченных черных шаров. Вычислить математическое ожидание и дисперсию, построить функцию распределения.
2. Три стрелка произвели по одному выстрелу в мишень. Вероятность попадания в нее первым стрелком равна 0,5; вторым - 0,4; третьим – 0.7. Какова вероятность того, что в результате стрельбы было два попадания?
3. Известен ряд распределения случайного вектора (x,h)

x \ h
-1	1/16		1/16
	1/48	1/24	1/48
		3/8
	3/8		1/24

Построить ряд распределения вектора с компонентами х = xh и у = x+h.

Задание 17.

1. В ящике 10 деталей, среди них 5 бракованных. Деталь вынимают и обследуют, затем возвращают в ящик. Составить закон распределения случайной величины X, представляющей собой количество обследованных деталей до появления бракованной. Вычислить математическое ожидание и дисперсию, а также построить функцию распределения.
2. Две игральных кости подбрасывают 4 раза. Найти вероятность того, что хотя бы один раз появится хотя бы одна «шестерка».
3. Известен ряд распределения случайного вектора (x,h)

x \ h
-1	1/16		1/16
	1/48	1/24	1/48
		3/8
	3/8		1/24

Построить ряд распределения случайного вектора с компонентами х = x+h и у = xh.

Задание 18.

1. Рабочий обслуживает 4 станка. Вероятность того, что в течение часа первый станок не потребует регулировки равна 0,9 , второй – 0,8 , третий – 0,75, четвертый – 0,7. Составить закон распределения случайной величины X – числа станков, которые в течение часа не потребуют регулировки. Вычислить математическое ожидание и дисперсию, а также построить функцию распределения.
2. Какие события независимы сами с собой?
3. Известен ряд распределения случайного вектора (x,h)

x \ h
-1	1/16		1/16
	1/48	1/24	1/48
		3/8
	3/8		1/24

Построить ряд распределения случайного вектора с компонентами х = x+h и у = x-h.

Задание 19.

1. В партии, состоящей из 16 деталей, имеется 4 бракованных. Наугад извлекают 5 деталей. Составить закон распределения случайной величины X, представляющей собой количество бракованных деталей среди 5 выбранных. Вычислить математическое ожидание и дисперсию, а также построить функцию распределения.

2. Два охотника из одинаковых ружей стреляют в медведя. В результате медведь был убит одной пулей. Как охотники должны разделить шкуру медведя, если вероятность попадания одного из них 0,3, а второго – 0,6?

1. Известен ряд распределения случайного вектора (x,h)

x \ h
-1	1/16		1/16
	1/48	1/24	1/48	1/24
		3/8		3/8

Построить ряд распределения случайного вектора с компонентами х = x+h и у = xh.

Задание 20.

1. В группе из 6 изделий имеется 2 бракованных. Чтобы обнаружить бракованное изделие, наугад берут одно изделие за другим и проверяют. Построить ряд распределения случайной величины X, представляющей собой количество проверенных изделий до обнаружения бракованного. Вычислить математическое ожидание и дисперсию, а также построить функцию распределения.
2. Из урны, содержащей 6 белых и 4 черных шара, последовательно без возвращения извлекают шары до появления первого белого шара. Какова вероятность того, что было произведено 3 извлечения?
3. Известен ряд распределения случайного вектора (x,h)

x \ h
-1	1/16		1/16
	1/48	1/24	1/48	1/24
		3/8		3/8

Построить ряд распределения случайного вектора с компонентами х = x+h и у = x-h.

Задание 21.

1. В ящике 8 деталей, среди них 2 бракованных. Деталь вынимают и обследуют, затем возвращают в ящик. Составить закон распределения случайной величины X, представляющей собой количество обследованных деталей до появления бракованной. Вычислить математическое ожидание и дисперсию, построить функцию распределения.
2. Что вероятнее: выиграть у равносильного противника не менее трех партий из четырех или не менее пяти партий из восьми?
3. Известен ряд распределения случайного вектора (x,h)

x \ h
-1	1/16		1/16
	1/48	1/24	1/48	1/24
		3/8		3/8

Найти D(x+h).

Задание 22.

1. Из урны, содержащей 6 белых и 4 черных шара, последовательно без возвращения извлекают шары до появления первого белого шара. Составить закон распределения случайной величины X – числа извлеченных черных шаров. Вычислить математическое ожидание и дисперсию, построить функцию распределения.
2. По самолету производится три выстрела. Вероятность попадания при первом выстреле равна 0,5, при втором – 0,б, при третьем – 0,8. При одном попадании самолет будет сбит с вероятностью 0,3, при двух – с вероятностью 0,6, при трех – с вероятностью 1. Какова вероятность того, что самолет будет сбит?
3. Из урны, содержащей 2 красных и 3 черных шара последовательно, без возвращения извлекают 3 шара. Случайная величина x - число белых шаров при первом и втором извлечениях, а случайная величина h - число черных шаров при втором и третьем извлечениях. Построить ряд распределения случайного вектора (x,h) и найти D(x+h).

Задание 23.