Использование производных для исследования функций
Возрастание, убывание функции. Точки экстремума
Достаточное условие возрастания, убывания и постоянства функции.Если в некотором промежутке производная данной функции больше нуля 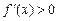 , то функция возрастает в этом промежутке; если производная меньше нуля
, то функция возрастает в этом промежутке; если производная меньше нуля 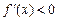 , то функция убывает. Если производная равна нулю, то функция постоянна на этом промежутке.
, то функция убывает. Если производная равна нулю, то функция постоянна на этом промежутке.
Определение.Точками экстремума функции называются точки максимума и минимума. На конечном промежутке у функции может быть несколько максимумов и минимумов, то есть экстремум имеет локальный характер.
Необходимое условие экстремума.Если  является точкой экстремума функции
является точкой экстремума функции 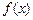 , то ее первая производная
, то ее первая производная  в этой точке равна нулю или не существует. Точки экстремума называются критическими точками.
в этой точке равна нулю или не существует. Точки экстремума называются критическими точками.
Достаточное условие экстремума.Если производная функции при переходе через критическую точку  меняет знак с плюса на минус, то есть
меняет знак с плюса на минус, то есть
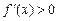 при
при 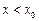 и
и 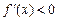 при
при 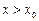 ,
,
то функция в этой точке имеет максимум.
Если производная функции при переходе через критическую точку меняет знак с минуса на плюс, то есть
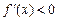 при
при 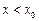 и
и 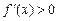 при
при 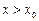 ,
,
то в этой точке функция имеет минимум.
Пример 4.1. Найти интервалы возрастания и убывания и экстремум функции  .
.
Решение.
Находим производную функции:
 .
.
Решая уравнение 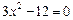 , получаем две точки возможного экстремума
, получаем две точки возможного экстремума 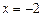 и
и  .
.
Исследовав знак 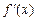 (рисунок 4.1.), получаем, что на интервалах
(рисунок 4.1.), получаем, что на интервалах 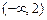 и
и 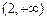 функция
функция 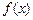 возрастает, а на интервале
возрастает, а на интервале  - убывает.
- убывает.
 Рисунок 5.1 Рисунок 5.1 |
Точка 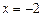 - точка максимума,
- точка максимума,  - максимальное значение функции, а точка
- максимальное значение функции, а точка  - точка минимума,
- точка минимума,  - минимальное значение функции.
- минимальное значение функции.
Выпуклость, вогнутость функции. Точки перегиба
Определение. График функции  будет выпуклым (или вогнутым) на интервале
будет выпуклым (или вогнутым) на интервале 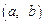 , если любая касательная к кривой
, если любая касательная к кривой  на этом интервале проходит выше или ниже этой кривой относительно оси абсцисс.
на этом интервале проходит выше или ниже этой кривой относительно оси абсцисс.
Достаточное условие выпуклости (вогнутости).Если вторая производная функции  в интервале
в интервале 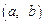 , то график функции
, то график функции  на этом интервале вогнут. Если
на этом интервале вогнут. Если  , то график функции выпуклый.
, то график функции выпуклый.
Определение.Точка кривой, где выпуклость меняется на вогнутость или наоборот, называется точкой перегиба.
Достаточное условие точки перегиба.Если вторая производная функции  в точке
в точке  равна нулю,
равна нулю,  , и меняет знак при переходе через эту точку, то эта точка
, и меняет знак при переходе через эту точку, то эта точка  является точкой перегиба графика функции.
является точкой перегиба графика функции.
Пример 4.2.Найти точки перегиба функции  .
.
Решение.Находим производную функции:  .
.
Находим вторую производную функции:  . Решая уравнение
. Решая уравнение  , получаем точку
, получаем точку 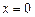 . Получаем, что
. Получаем, что 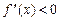 на интервале
на интервале  ,
, 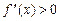 на интервале
на интервале 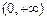 . Следовательно
. Следовательно 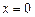 - точка перегиба функции.
- точка перегиба функции.
