Тема 5.2. Случайные события. Классическое определение вероятности.

Классическое определение вероятности. Вероятностью события А называют отношение

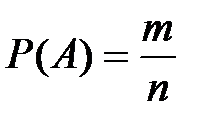,где п – число всех равновозможных элементарных исходов, образующих полную группу попарно несовместных событий, т – число исходов, благоприятствующих событию А из п равновозможных исходов.

Из определения следует, что .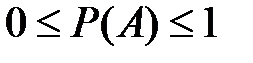

Статистическое определение вероятности. Пусть данный опыт при одних и тех же условиях повторяют N раз (серия опытов) и событие А произошло М раз. Тогда величину

называют относительной частотой или частостью события А. При увеличении числа опытов N частость 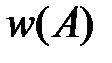приближается к , поэтому на практике считают

.

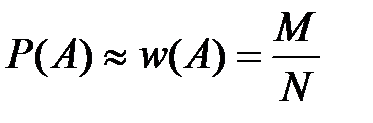Случайным называют событие, которое может произойти или не произойти в результате некоторого испытания (опыта). Их обозначают заглавными буквами А В С Д … (латинского алфавита).

Событие называется достоверным, если оно обязательно произойдет в результате данного испытания.

Событие называется невозможным, если оно не может произойти в результате данного испытания.

Событие 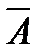называется противоположным к событию А, если оно происходит тогда и только тогда, когда не происходит А, и наоборот.

Два события А и В называют совместными, если они могут произойти одновременно, при одном исходе эксперимента, и несовместными, если они не могут произойти одновременно ни при одном исходе эксперимента.

Суммой (объединением) нескольких событий называется событие, состоящие в наступлении хотя бы одного из них в результате испытания. ( , )

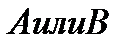Если события А и В совместны, то сумма А+В означает, что наступает событие А, или событие В, или оба события вместе.

Если события несовместны, то событие А+В заключается в том, что наступить А или В, тогда + заменяется словом «или».

Вероятность суммы двух событий вычисляется по формуле (теорема сложения)

.

Если события несовместны, то Р(АВ) = 0 и Р(А + В) = Р(А) + Р(В).

Произведением (пересечением) нескольких событий называется событие, состоящие в совместном наступлении всех этих событий в результате испытания.

Помимо обычной (безусловной) вероятности можно рассматривать так называемую условную вероятность, вычисляемую при условии, что событие B произошло. Такую вероятность (вероятность А при условии В) обозначают Р(А|В) и вычисляют с помощью одной из двух формул:

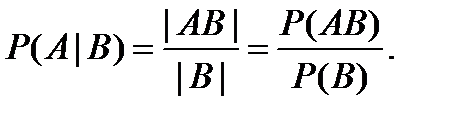
Из этой формулы вытекает формула для вероятности произведения двух событий (теорема умножения)

.

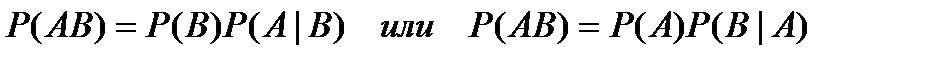Формула умножения для трех событий:

.

Событие А не зависит от В, если появление события В не меняет значения вероятности события А, т.е. условная вероятность равна безусловной: Р(А/В) = Р(А). Аналогично определяется независимость события B от A. Оказывается, что свойство независимости на самом деле симметрично относительно событий A и B, и потому определение независимости двух событий принимает более простой вид:

Два события A и B независимы, если справедливо равенство Р(АВ) = Р(А) × Р(В).

Контрольные вопросы:

1. Сформулируйте классическое определение вероятностей. Укажите недостатки этого определения.

2. Какое событие называется достоверным, невозможным, случайным?

3. Дайте определение полной группы событий.

4. Какие события называются несовместными, совместными, противоположными, независимыми?

5. Дайте определение относительной частоты.

6. Сформулируйте статистическое определение вероятностей. Назовите условия существования статистической вероятности.

7. Сформулируйте теоремы о вероятности сумы двух совместных, несовместных событий.

8.Сформулируйте теорему умножения вероятностей.