Сложить все полученные произведения

Таким образом, можем записать формулу для нахождения математического ожидания: 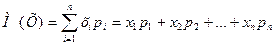, где х_i – варианты, р_i – частоты соответствующих вариант, i – порядковые номера вариант.

Приведем еще один пример.

Пример 5. Найти размах, моду и математическое ожидание выборки:

4, 6, 3, 8, 4, 3, 5, 4, 5, 6, 4, 3, 6, 5, 4, 3, 5, 7, 8, 4.

Решение. Всего имеется 20 результатов, самый маленький из которых равен 3, а самый большой равен 8. Размах равен 8 – 3 = 5. Мода, т. е. наиболее часто встречающееся значение в выборке, равна 4. Эта варианта встречается 6 раз. Посчитаем среднее значение, составив таблицу распределения вариант.

Варианта
Частота варианты	0,2	0,3	0,2	0,15	0.05	0,1

Значит, среднее значение выборки равно

.

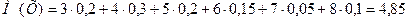Ответ: 5; 4; 4,85.

Математическое ожидание является мерой концентрации (центрирования) случайной величины Х, заданной выборкой. Смысл характеристики математического ожидания заключается в следующем: это точка на числовой оси, около которой, как правило, концентрируется большинство значений дискретной случайной величины.

Свойства математического ожидания:

1⁰ М(С) = С, где С – const.

2⁰ М(СХ) = СМ(Х).

3⁰ М(X + Y) = M(X) + M(Y).

4⁰ M(X + C) = M(X) + C.

Еще одной важной характеристикой выборки является дисперсия выборки (дискретной случайной величины Х).

Дисперсией дискретной случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания.

.

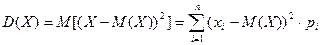Дисперсия является мерой разброса (рассеивания) значений случайной величины Х относительно ее математического ожидания.

Свойства дисперсии:

1⁰ D(С) = 0.

2⁰ D(СХ) = С²D(Х).

3⁰ D(X + C) = D(X).

4⁰ D(X) = M(X²) – (M(X))².

Мы составили простейший «паспорт» выборки. В него входит размах, мода, среднее значение выборки. Среди других подобных «паспортных данных» выборки упомянем еще ее медиану или середину выборки.Ограничимся выборками, в которых все варианты однократны. Если число таких вариант нечетно, скажем 29, то медиана равна пятнадцатой по счету варианте. Если же число вариант четно, скажем 30, то медиана равна полусумме (или среднему арифметическому) пятнадцатой и шестнадцатой по счету вариант. В любом случае, слева и справа от медианы находится одинаковое число вариант этой выборки. Это и есть основное свойство медианы выборки. Основное преимущество медианы – ничего не надо считать для ее нахождения. Следует просто упорядочить варианты выборки и потом разделить их на две равные группы. Есть у выборок и другие, более подробные характеристики.

Пример 6. Для дискретной случайной величины Х из примера 4 найти медиану и дисперсию.

Решение. Запишем вариационный ряд: 3, 4, 5, 6, 7, 8. Так как он состоит из четного числа вариант, то возьмем средние значения ряда и найдем их среднее арифметическое: . Для нахождения дисперсии дополним таблицу еще двумя строками (М(Х) = 4,85):

Варианта
Кратность варианты
Частота варианты	0,2	0,3	0,2	0,15	0.05	0,1
хi – М(Х)	-1,85	-0,85	0,15	1,15	2,15	3,15

.

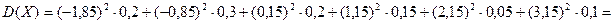
Ответ: 5,5; 2,3275.