Основные теоремы теории вероятностей
СЛУЧАЙНЫЕ СОБЫТИЯ.
[1], Гл. I
Основные понятия теории вероятностей
Предварительно необходимо повторить теорию соединений по любому курсу алгебры для средней школы.
В практической деятельности мы часто сталкиваемся со случайными событиями, т.е. событиями, которые могут произойти или не произойти в результате опыта по причинам, не поддающимся учету в данных условиях опыта.
Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех единственно возможных и невозможных элементарных исходов опыта.
Таким образом, вероятность события А определяется формулой:
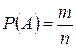, (1)
где m – число исходов опыта, благоприятствующих событию А,
n – число всех возможных исходов опыта.
Формула (1) имеет ограниченную область применения. Она предполагает, что опыт распадается на конечное число равновозможных исходов. На практике эти условия часто не выполняются, и для приближенного вычисления вероятности события определяют его частоту.
Пусть произведена серия из N опытов, в каждом из которых могло появиться или не появиться некоторое событие А. Частотой события А называется отношение числа опытов М, в которых появилось событие А, к общему числу произведенных опытов. Частота события определяется формулой:
. (2)
При небольшом числе опытов частота события носит случайный характер. Однако при увеличении числа опытов частота все более теряет свой случайный характер, стабилизируется, приближаясь с незначительными колебаниями к постоянной величине, равной вероятности этого события.
Таким образом, если опытным путем установлена относительная частота, то полученное число можно принять за приближенное значение вероятности.
Задача 1
Из букв разрезанной азбуки составлено слово «книга». Ребенок, не умеющий читать, рассыпал это слово и собрал его наудачу. Какова вероятность того, что снова получилось слово «книга»?
Р е ш е н и е
Общее число возможных элементарных исходов опыта равно числу перестановок из 5 элементов 
, а число исходов, благоприятствующих событию, равно единице, так как при единственном порядке букв можно прочесть слово «книга».
Искомая вероятность:
.
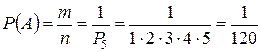Вывод: При многочисленном повторении опыта примерно один раз на 120 случаев читаем слово «книга». Например, если повторить опыт 1000 раз, то примерно в 8-ми – 9-ти случаях прочтем слово «книга».
Задача 2
Набирая номер телефона, абонент забыл последние две цифры, и помня, что они разные, набрал их наудачу. Какова вероятность того, что он набрал нужный номер?
Р е ш е н и е
Общее число всевозможных исходов опыта равно числу размещений из 10 по 2, т.е.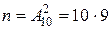 
. Число исходов, благоприятствующих событию, равно единице.
Искомая вероятность:
.
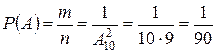Вывод: При большом числе опытов частота события будет колеблясь приближаться к постоянной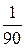 
.
 |
Задача 3
В ящике имеется 15 сверл, 8 из них высшего качества. Наудачу взяли 3 сверла. Найти вероятность того, что все 3 взятые сверла окажутся высшего качества.
Р е ш е н и е
Так как порядок здесь роли не играет, то общее число всевозможных исходов будет равно числу сочетаний из 15 по 3, т.е.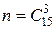 
, а число благоприятствующих событию исходов равно тоже числу сочетаний из 8 по 3 (8 сверл высшего качества, любая комбинация из 8 по 3 будет благоприятствовать выполнению события).
Искомая вероятность:
.
Вывод: На каждые 65 опытов, каждый из которых состоит в случайном отборе трех сверл, примерно 8 опытов будут такими, когда взятые сверла окажутся высшего качества.
Задача 4
В группе 15 студентов, 8 из них отличники. Наудачу (по списку) вызвали 6 студентов. Найти вероятность того, что 4 студента из вызванных окажутся отличниками.
Р е ш е н и е
Число всевозможных исходов опыта здесь также равно числу сочетаний из 15 по 6, (порядок вызова роли не играет)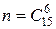 
.
Число благоприятствующих исходов здесь находится несколько сложнее. Благоприятной считаем такую комбинацию, в которой 4 студента отличники (любые), а 2 – нет, 4 отличника можно выбрать из 8 отличников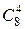 
способами, при этом остальные 6-4=2 студента (не отличники) выбираем из 15-8=7 студентов 
способами.
Если в каждой четверке отличников присоединить одну из пар студентов, не отличников, то получим «благоприятные» группы из 6 человек. Их число равно 
.
Искомая вероятность:
.
Основные теоремы теории вероятностей
[1], Гл. II, III, IV
Перед изучением теоремы уясните понятия суммы и произведения событий. Суммой А + В двух событий называют событие С, состоящее в появлении события А или события В, или обоих вместе.
Если появление события А не исключает появление события В, то такие события называются совместными. В противном случае события назовем несовместными. Например, Иванов и Петров спят в одной комнате. Звонит будильник. Событие А – проснулся Иванов, В – проснулся Петров. Суммой этих событий С=А+В будет событие, состоящее в том, что проснулся или Иванов (Петров спит), или Петров (Иванов спит), или оба проснулись (так как события А и В совместные). При решении задач сложение событий надо применять там, где напрашивается слово «или».
Произведением двух событий А и В называют событие С=АВ, состоящее в совместном появлении этих событий. Для приведенного примера АВ – событие, состоящее в том, что проснулись оба (и Иванов и Петров). Где напрашивается союз «и», там надо рассматривать произведение событий.
Хорошо усвойте и запомните понятие противоположного события:
Событие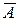 
назовем противоположным событию А, если их сумма является достоверным событием, то есть
.
Например, опыт состоит в бросании игральной кости. Если событие А – кубик выпал гранью с цифрой «6», то событие 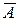- кубик выпал гранью, на которой возможны цифры от 1 до 5.
Повторите и докажите самостоятельно теоремы сложения и умножения, теорему полной вероятности и формулу Байеса.
Задача 1
При увеличении напряжения в 2 раза соответственно с вероятностями 0,3; 0,4; 0,6; может произойти разрыв электрической цепи вследствие выхода из строя одного из трех последовательно соединенных элементов. Определить вероятность того, что при этом не будет разрыва в цепи. Как изменится искомая вероятность, если не будет первого элемента?
Р е ш е н и е
Найдем вероятность того, что не будет разрыва цепи 
, По условию задачи 
, 
, 
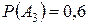. Разрыва цепи не будет, если не выйдут из строя все три элемента ( и I-ый, и II-ой, и III-й). События 
, 
, 
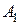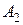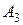независимые, значит
.
Если не будет первого элемента, то искомая вероятность (невыхода из строя и II-го и III-го элементов) равна:
.
Вероятность того, что в цепи не будет разрыва, возросла.
Задача 2
Вероятность того, что книга имеется в фондах первой библиотеки, равна 0,5; в фондах второй – 0,7; в фондах третьей – 0,4. Определить вероятность наличия книги в фондах:
1) хотя бы одной библиотеки (соб. А);
2) только одной библиотеки (соб. В).
Р е ш е н и е
1) Вероятность события А проще находить через вероятность противоположного события. Пусть 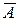- книги нет ни в одной библиотеке. По условию 
; 
; 
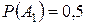. Тогда 
; 
; 
; 
.
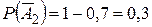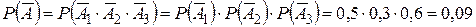События 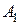, , 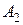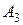совместны, так как книга может оказаться по всех библиотеках. Значит событие А заключается в том, что книга имеется в любой одной, двух или всех трех библиотеках, то есть
.
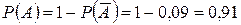2) Наличие книги только в одной библиотеке (событие В) заключается в том, что книга имеется в первой библиотеке, и тогда ее нет в остальных двух и т.д.
.
События – слагаемые несовместны, а события – множители независимые. Тогда
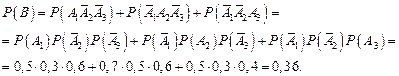
Вероятность наличия книги в фонде только одной библиотеки значительно меньше, так как требования более жесткие.
Задача 3
В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить норму для каждого спортсмена равна соответственно 0,9; 0,8; 0,75.
Найти вероятность того, что спортсмен, вызванный наудачу, выполнит норму.
Р е ш е н и е
Может оказаться три случая (гипотезы):
- вызванный спортсмен окажется лыжником;
- вызванный спортсмен окажется велосипедистом;
- вызванный спортсмен окажется бегуном.
Всего спортсменов 30, следовательно, вероятности гипотез равны:
.
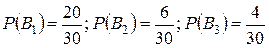Убедимся, что совокупность гипотез составляет полную группу событий:
.
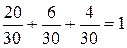Пусть А – событие, состоит в том, что спортсмен, вызванный наудачу, выполнит норму. Это событие наступит одновременно с наступлением одной из трех гипотез. Условные вероятности равны:
.
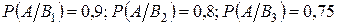По формуле полной вероятности:
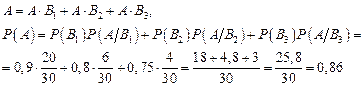
О т в е т: 
.
Задача 4
Используем условие задачи 3, но теперь известно, что некий спортсмен, вызванный наудачу, выполнил норму. Найти вероятность того, что этот спортсмен
а) лыжник (соб. );
б) велосипедист (соб. );
в) бегун (соб. ).
Р е ш е н и е
Возможны те же три гипотезы 
, которые имели место в задаче 3. Но теперь известно, что событие А свершилось. Необходимо переоценить вероятности гипотез по формуле Байеса:
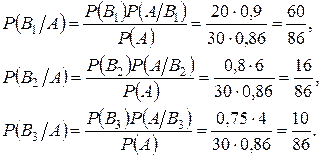
Проверка: 
.
Замечание. Формула Байеса является следствием формулы полной вероятности и применяется тогда, когда при наличии полной группы гипотез, способствующих появлению события А с определенными вероятностями, известно, что в результате опыта событие А наступило.
По формуле Байеса производим пересчет вероятностей гипотез после опыта.