Основные задачи регрессионного анализа

В силу неоднозначности корреляционной зависимости между Y и X, для изучения влияния независимой переменной на объясняемую переменную используют «усредненные» зависимости, т.е. изучают условное математическое ожидание M[Y|X=x] (математическое ожидание случайной величины, вычисленную в предположении, что переменная X приняла значение x) в зависимости от x. Поскольку при различных значениях будут получаться различные значения условного математического ожидания, то мы будем иметь дело с некой функцией

, (5.1)

которая называется функцией регрессии Y на X.

Отметим, что реальные значения зависимой переменной Y не всегда совпадают с ее условными математическими ожиданиями и могут быть различными при одном и том же значении объясняющей переменной. Поэтому связь между зависимой и объясняющей переменной обычно записывают в виде

, (5.2)

называемое теоретическим уравнением регрессии. Величину e обычно называют случайным отклонением (ошибкой, возмущением). Это слагаемое, которое, по существу, является случайной величиной и указывает на стохастическую суть зависимости.

Возникает вопрос о причинах присутствия в регрессионных моделях случайного отклонения. Среди таких можно отметить следующие.

1. Невключение в модель всех объясняющих переменных. Отсутствие в модели «важных» факторов, оказывающих существенное влияние на результат. Парная регрессия почти всегда является большим упрощением. В действительности существуют и другие факторы, которые не учтены в уравнении (5.2). Проблема состоит ещё и в том, что никогда заранее не известно, какие факторы при создавшихся условиях действительно являются определяющими, а какими можно пренебречь. Здесь уместно отметить, что в ряде случаев учесть непосредственно какой-то фактор нельзя в силу невозможности получения по нему статистических данных. Например, величина сбережений домохозяйств может определяться не только доходами их членов,но и, например, здоровьем последних, информация о котором в цивилизованных странах составляет врачебную тайну и не раскрывается. Кроме того,ряд факторов носит принципиально случайный характер (например, погода), что добавляет неоднозначности при рассмотрении некоторых моделей (например, модель, прогнозирующая объем урожая).

2. Неправильный выбор функциональной формы модели. Из-за слабой изученности исследуемого процесса либо из-за его переменчивости может быть неверно подобрана функция, его моделирующая. Это, безусловно, скажется на отклонении модели от реальности, что отразится па величине случайного отклонения e. Например, производственная функция (Y) одного фактора (X)может моделироваться функцией , хотя должна была использоваться другая модель: , учитывающая закон убывающей эффективности.

3.Агрегирование переменных. Во многих моделях рассматриваются зависимости между факторами, которые сами представляют сложную комбинацию других, более простых переменных. Например,зависимость между урожайностью и количеством внесенных удобрений индивидуальна для различных полей и любая попытка определить зависимость между совокупным урожаем и совокупным внесением удобрений является лишь приближением (аппроксимацией).

4. Ошибки измерений. Какой бы качественной ни была модель, ошибки измерений переменных отразятся на несоответствии модельных значений эмпирическим данным, что также отразится на величине случайного отклонения. В практическом использовании регрессионных методов ошибки измерений представляют наибольшую опасность. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки – увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Особенно велика роль ошибок измерения при исследовании на макроуровне. Так, в исследованиях спроса и потребления в качестве объясняющей переменной широко используется «доход на душу населения». Вместе с тем статистическое измерение величины дохода сопряжено с рядом трудностей и не лишено возможных ошибок, например, в результате наличия сокрытых доходов.

Для определения параметров функции регрессии необходимо знать и использовать все значения переменных X и Y генеральной совокупности, что практически невозможно. Основные задачи регрессионного анализа состоят в том, чтобы по имеющимся статистическим данным для переменных X и Y:

а) установить форму зависимости между переменными;

б) оценить функцию регрессии (т.е. получить наилучшие оценки неизвестных параметров, проверить статистические гипотезы о параметрах модели);

в) проверить, достаточно ли хорошо модель согласуется со статистическими данными (адекватность модели данным наблюдений);

г) оценить неизвестные значения зависимой переменной (сделать прогноз значений).

Используя выборочные данные можно построить так называемое эмпирическое уравнение регрессии:

, (5.3)

где 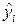– оценка условного математического ожидания , – оценка функции регрессии. Следовательно, в конкретном случае

, (5.4)

где отклонение e_i – оценка теоретического случайного отклонения e_i. Эту величину также называют остатками (residuals).

Решений задачи построения качественного уравнения регрессии, соответствующего эмпирическим данным и целям исследования, является достаточно сложным и многоступенчатым процессом. Его можно разбить на три этапа:

1) выбор формулы уравнения регрессии (спецификация);

2) определение параметров выбранногоуравнения (параметризации);

3) анализ качества уравнения и поверка адекватности уравнения эмпирическим данным, совершенствование уравнения (верификации).

В случае парной регрессия выбор формулы обычно осуществляетсяпо графическому изображению реальных статистических данных в виде точек в декартовой системе координат, которое называется корреляционным полем (диаграммой рассеивания)(см., например, рис. 5.1).

Рис. 5.1

На рис. 5.1 представлены три ситуации.

На графике 5.1, а взаимосвязь между Х и Y близка к линейной, и прямая 1 достаточнохорошо соответствуетэмпирическим точкам. Поэтому в данном случае в качестве зависимости между Х и Y целесообразно выбрать линейную функцию .

На графике 5.1, б реальная взаимосвязь между Х и Y, скорее всего, описывается квадратичной функцией (линия 2). И какую бы мы ни провели прямую (например, линия I), отклонения точек наблюдений от нее будут существенными и неслучайными.

На графике 5.1, в явная взаимосвязь между Х и Y отсутствует. Какую бы мы ни выбрали форму связи, результаты ее спецификации и параметризации (определение коэффициентов уравнения) будут неудачными. В частности, прямые 1 и 2, проведенные через центр «облака» наблюдений и имеющие противоположный наклон, одинаково плохи для того, чтобы делать выводы об ожидаемых значениях переменной Y по значениям переменной X.

Более подробно вопросы спецификации, а также вопросы параметризациии верификации уравнения регрессии, будут обсуждены в следующих лекциях.