Решение системы с помощью обратной матрицы
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение.
Пример 11:
Решить систему с матричным методом
.
Решение: Запишем систему в форме матричного произведения: 
, где
.
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаем, всем понятно.
Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице 
нужно поставить нули.
Решение системы найдем по формуле: 
. Согласно формуле нам нужно найти обратную матрицу 
и выполнить матричное умножение 
.
Алгоритм нахождения обратной матрицы подробно разобран на уроке Вычисление обратной матрицы. Обратную матрицу найдем по формуле: 
где |A| – определитель матрицы A, Ã – матрица алгебраических дополнений исходной матрицы, а ÃT – присоединённая матрица, или транспонированная матрица алгебраических дополнений соответствующих элементов матрицы A.
Сначала разбираемся с определителем:
.
Здесь определитель раскрыт по первой строке.
Внимание! Если
, то обратной матрицы не существует, и решить систему матричным методом невозможно.В этом случае для получения соотношений между неизвестными применяетсяметод исключения неизвестных (метод Гаусса).
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
.
Как мы уже обозначали, первая цифра в символе элемента – это номер строки, в которой находится данный элемент, а вторая цифра – это номер столбца, в котором находится данный элемент:
Так, например, элемент M13 находится на пересечении первой строки и третьего столбца, а элемент M32 находится на пересечении третей строки и второго столбца.
, 
, 
, 
, 
, 
, 
Порядок расчета миноров совершенно не важен, здесь мы их вычислили слева направо по строкам. Таким образом:
– это матрица миноров соответствующих элементов матрицы A;
– матрица алгебраических дополнений, а
– транспонированная матрица алгебраических дополнений.
Выполненные шаги мы подробно разбирали на уроке Вычисление обратной матрицы. Теперь записываем обратную матрицу:
Не вносим 
в матрицу, это серьезно затруднит дальнейшие вычисления.Деление нужно было бы выполнить, если бы все числа матрицы делились на 60 без остатка. А вот внести минус в матрицу в данном случае нужно, это, наоборот – упростит дальнейшие вычисления. Осталось провести матричное умножение.
Обратите внимание, что деление на 60 выполняется в последнюю очередь.
Пример 12:
Решить систему с помощью обратной матрицы.
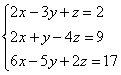
Это пример для самостоятельного решения (ответ в конце урока).
Ответы:
Пример 3: 
.
Пример 6: 
.
Пример 8: 
, 
.
Примеры 10, 12: 