Критический диаметр тепловой изоляции

Тепловой изоляцией является покрытие из теплоизоляционного материала, которое способствует снижению потерь в окружающую среду.

Пусть труба покрыта слоем тепловой изоляции (рис. 2.7, а).

Теплопотери (Q, Вт) через теплоизолированную стенку трубы можно представить формулой

(2.36)

где

(2.37)

Графическая зависимость R=f(d_из) представлена на рис. 2.7, б, откуда следует, что термическое сопротивление изоляции с увеличением диаметра изоляции может уменьшаться до минимального значения, а затем увеличиваться. Так как теплопотери (Q) обратно пропорциональны термическому сопротивлению (R) согласно (2.36), то зависимость Q=f(d_из) является зеркальным отображением кривой R=f(d_из).

Значение d_из , соответствующее минимуму кривой R=f(d_из), называется критическим диаметром d_кр и может быть определено из условия минимума функции

(2.38)

Совместное решение (2.38) и (2.37) дает

откуда

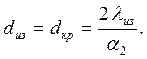(2.39)

Критическому диаметру изоляции соответствует минимальное термическое сопротивление и максимальный тепловой поток.

Анализ уравнения (2.37) показывает:

а) при наложении тепловой изоляции толщиной δ_из на трубу с d₂<d_кр (рис. 2.7, б) термическое сопротивление уменьшается, теплопотери увеличиваются, т.к. увеличивается площадь теплоотдающей поверхности изоляции
(π d_из );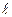

б) если d₂>d_кр , термическое сопротивление увеличивается, теплопотери уменьшаются, тепловая изоляция оправдывает свое назначение, т.к. третье слагаемое в уравнении (2.37) становится существенно больше, чем четвертое.

Таким образом, тепловая изоляция уменьшает теплопотери, если
d₂ d_кр,

откуда

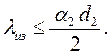(2.40)

Правильно подобранный теплоизоляционный материал должен удовлетворять условию (2.40).

Контрольные вопросы и задания

1. Как изменяется термическое сопротивление плоской стенки: а) с увеличением толщины стенки (δ); б) с увеличением коэффициента теплопроводности (λ)? Сравните термическое сопротивление пластин одинаковой толщины из текстолита и стали.

2. Как рассчитать передаваемую теплоту через плоскую стенку за одни сутки, если известны температуры на поверхностях стенки (t₁ и t₂), толщина стенки (δ), коэффициент теплопроводности (λ), площадь изотермической поверхности (F)?

3. Рассчитайте эффективный коэффициент теплопроводности (λ_эф) для конденсатора, набранного из 7 дюралевых листов толщиной δ₁=1,5мм с теплопроводностью λ₁=174 Вт/м· К, между которыми находится пропиточная бумага с толщиной слоев δ₂=3мм, λ₂=0,116 Вт/м· К. Ответ: λ_эф=0,184 Вт/м· К.

4. Тепловой поток, передаваемый теплопроводностью через цилиндрическую или плоскую стенку, рассчитывается по формуле Запишите формулы для термического сопротивления (R) плоской и цилиндрической стенок.

5. Температура внутренней поверхности цементной трубы t₁=50^oC, наружной – t₂=-20^oC. Запишите уравнение, по которому можно рассчитать радиус изотермической поверхности с температурой t=0^оС.

6. Что можно сказать о температурах среды (t_ж) и поверхности стенки (t_с) при условии ?

7. Запишите формулу для коэффициента теплопередачи многослойной плоской стенки.

8. Запишите термическое сопротивление теплопроводности и термическое сопротивление теплоотдачи цилиндрической стенки. Какие перепады температур они определяют?

9. Наложение электроизоляции на кабели и провода с d₂<d_кр улучшает их охлаждение, снижает температуру. При каком диаметре изоляции охлаждение будет максимальным, а температура минимальной? Какому условию по λ_из должен удовлетворять правильно подобранный электроизоляционный материал?