Факторы, влияющие на точность решения
1 Округление результатов вычислений.
2 Неточность исходных данных, которая в ряде случаев может вызвать несоразмерное снижение точности решения.
1 Округление результатов вычислений
Как видно из рассмотренного элементарного примера, в качестве ведущего элемента на к-ом шаге прямого хода берётся элемент akk(к-1) , и к нему для выполнения шагов прямого хода предъявляются условия:
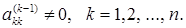
Если выбранный элемент 
близок или равен нулю, то решение получаем с недопустимой погрешностью, либо оно вообще не может быть получено. Для устранения чрезмерной погрешности применяется вычислительная схема главного элемента. В качестве ведущего элемента берется наибольший по абсолютной величине (по модулю) коэффициент 
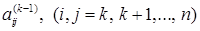Чтобы он занял место ведущего элемента необходима перестановка строк и столбцов матрицы коэффициентов. В связи со сложностью программной реализации схемы главного элемента на практике применяются её модификации, называемые вычислительной схемой с частичным выбором главного элемента. В качестве ведущего берется наибольший по модулю коэффициент 
либо к-ого столбца, т.е. , где i = k, k+1, …, n, j = k, либо к-ой строки, т.е. , где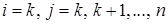 
, либо главной диагонали, т.е. , где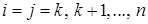 
. Выбор модификации определяется особенностями матрицы а.
2Неточность исходных данных
Могут встречаться случаи, когда погрешности исходных данных, т. е. значений элементов матриц а и b приводят к чрезмерно большой погрешности. Большая погрешность наблюдается при плохой обусловленности матрицы коэффициентов системы уравнений.
Матрица коэффициентов системы уравнений плохо обусловлена, если определитель матрицы коэффициентов системы уравнений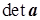 
меньше значения, определяемого следующим выражением (оценка Адамара):
Плохая обусловленность матрицы а может быть следствием либо некорректности математического описания задачи, либо специфичности рассматриваемого состояния системы, например, при расчете установившегося режима, близкого к предельному по условию существования. В первом случае необходимо составление корректного математического описания, соответствующего техническому существу задачи, а во втором — использование иных методов, а не метода Гаусса.
СПЕЦИФИКА УРАВНЕНИЙ УСТАНОВИВШЕГОСЯ РЕЖИМА ЭЛЕКТРИЧЕСКОЙ СИСТЕМЫ
1. В большом числе случаев матрица коэффициентов системы уравнений является слабозаполненной, т.е. содержит большое число нулевых элементов. Так в матрице Уy число ненулевых элементов равно примерно 4n, т.е. n2-4n элементы этих матриц равны нулю.
2. Диагональные элементы матрицы а обычно больше недиагональных.
3. Матрица коэффициентов симметричная – можно более рационально организовать вычислительный процесс прямого хода метода Гаусса. Учет этих особенностей при реализации метода Гаусса на ЭВМ существенно повышает вычислительную эффективность программы за счет сокращения требуемого объема памяти и времени расчёта.
УЧЁТ СЛАБОЙ ЗАПОЛНЕННОСТИ (РАЗРЕЖЕННОСТИ)
МАТРИЦЫ УЗЛОВЫХ ПРОВОДИМОСТЕЙ Yу
1 Матрица узловых проводимостей находится в памяти машины в т.н. упакованном виде (ненулевые элементы матрицы запоминаются с помощью т.н. линейных связанных списков).
2 Стремятся так построить алгоритм, чтобы обеспечить минимальное возрастание заполненности матрицы а(к) в процессе прямого хода метода Гаусса.