Однородные системы линейных уравнений
Система линейных алгебраических уравнений вида
 (6.5)
(6.5)
называется однородной системой линейных алгебраических уравнений.
Очевидно, что однородная система всегда совместна, так как для нее всегда существует тривиальное решение  . Кроме того, она может иметь и нулевое решение.
. Кроме того, она может иметь и нулевое решение.
1. Однородная система имеет ненулевое решение тогда и только тогда, когда ранг матрицы системы меньше числа неизвестных, т.е.  , где
, где  , А – матрица системы.
, А – матрица системы.
2. Однородная система, в которой число уравнений равно числу неизвестных, имеет ненулевое решение тогда и только тогда, когда ее определитель  равен нулю.
равен нулю.
Пример. Решить систему  .
.
Решение. Система однородная, следовательно, она имеет единственное решение или множество решений. Для выяснения этого найдем ранг основной матрицы (он всегда равен рангу расширенной) и сравним его с числом неизвестных.
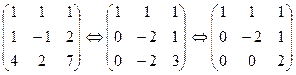
Ранг матрицы  и равен числу неизвестных, система имеет единственное нулевое решение.
и равен числу неизвестных, система имеет единственное нулевое решение.
Пример. Решить систему 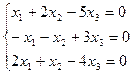 .
.
Решение:
Система однородная, всегда совместная. Исследуем, имеет ли она ненулевое решение. Преобразуем основную матрицу системы:

Так как  , а число неизвестных равно трем, то система имеет множество решений, среди которых будут и ненулевые. Восстановим систему по последней матрице:
, а число неизвестных равно трем, то система имеет множество решений, среди которых будут и ненулевые. Восстановим систему по последней матрице:
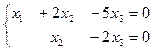
Из последнего уравнения 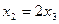 , из первого находим
, из первого находим  , где
, где 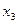 - любое число.
- любое число.
Задачи для практических занятий
и самостоятельной работы
Решить системы линейных алгебраических уравнений, используя формулы Крамера:
1. 
2. 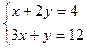
3. 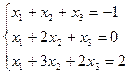
4. 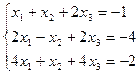
5. 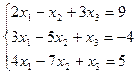
6. 
7. 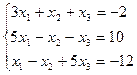
8. 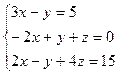
9. 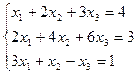
10. 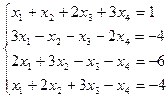
Решить системы линейных алгебраических уравнений матричным методом:
11. 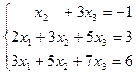
12. 
13. 
14. 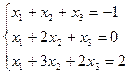
Решить системы линейных алгебраических уравнений методом Гаусса:
15. 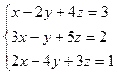
16. 
17. 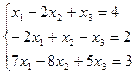
18. 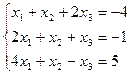
19. 
20. 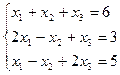
21. 
22. 
23. 
24. 
25. 
26. 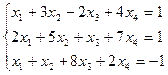
27. 
28. 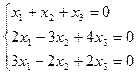
29. 
30. 
Ответы
1.  ,
, 
2. 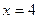 ,
, 
3. 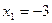 ,
, 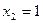 ,
, 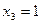
4.  ,
,  ,
, 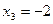
5. система несовместна
6.  ,
, 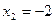 ,
, 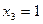
7. 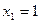 ,
, 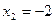 ,
, 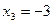
8.  ,
,  ,
, 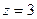
9. система несовместна
10. 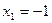 ,
,  ,
,  ,
, 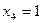
11. 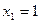 ,
,  ,
, 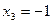
12. 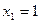 ,
,  ,
, 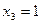
13.  ,
, 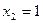 ,
, 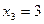
14. 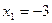 ,
, 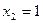 ,
, 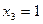
15. 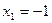 ,
, 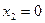 ,
, 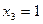
16.  ,
, 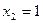 ,
, 
17. система несовместна
18. 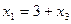 ,
,  ,
, 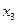 - любое число
- любое число
19.  ,
, 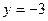 ,
, 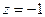
20. 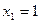 ,
,  ,
, 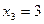
21. 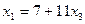 ,
, 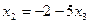 ,
, 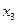 - любое число
- любое число
22. система несовместна
23. 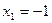 ,
, 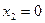 ,
, 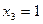
24. 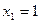 ,
,  ,
, 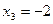
25. система несовместна
26.  ,
,  ,
, 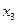 ,
,  - любые числа
- любые числа
27.  ,
, 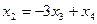 ,
, 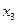 ,
,  - любые числа
- любые числа
28. 
29. 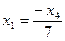 ,
, 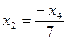 ,
,  ,
,  - любое число
- любое число
30. 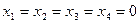
Литература
1. Бугров Я.С., Никольский С.М. Элементы высшей линейной алгебры и аналитической геометрии. – М.: Наука, 1980 г.
2. Головина Л.И. Линейная алгебра и некоторые ее приложения. – М.: Наука, 1979 г.
3. Фаддеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. – М.: Наука, 1977 г.
Учебное издание
Ивина Н.А.
Методические указания к практическим занятиям
РГТК, 2002 г. – 44 с.
Подписано в печать 06.09.2002 г. Формат А5
Бумага для офсетной печати
Отпечатано на ризографе.
Тираж 200 экземпляров. Заказ № 73
Рязанский государственный технологический колледж
390035 г. Рязань, пр. Гоголя, 6.
 Лицензия Б 794164 № 0001 от 18.03.99
Лицензия Б 794164 № 0001 от 18.03.99
 |
