Полная группа событий. Пространство элементарных исходов. Примеры
Полная группа событий. Полной группой событий называется совокупность всех возможных результатов опыта.
Теорема. Сумма вероятностей событий А1 , А2 , ..., Аn , образующих полную группу, равна единице:
Р (A1) + Р (А2) + ... + Р (Аn) = 1.
Пространство элементарных исходов
Теория вероятностей изучает случайные явления не непосредственно, а с помощью идеализированных математических моделей случайных опытов.
Всякий случайный опыт (испытание, эксперимент) состоит в осуществлении некоторого комплекса условий и наблюдении результата. Любой наблюдаемый результат опыта интерпретируется как случайный исход (случайное событие). Случайное событие в результате опыта может произойти, а может и не произойти.
Каждому опыту ставится в соответствие пространство элементарных исходов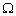 
. Это множество простейших (т.е. неразложимых в рамках данного опыта на более простые) взаимоисключающих исходов 
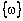, таких, что результатом эксперимента всегда является один и только один исход 
.
Пример 1.1.1.
Опыт состоит в бросании одной правильной шестигранной игральной кости и наблюдении числа выпавших очков.
Элементарные исходы: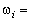 
{выпало 
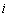очков}, 
.
Неэлементарные исходы (события):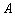 
={выпало чётное число очков}, 
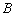={выпало число очков, большее, чем 2} и т.п. Исход 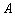не является элементарным, т.к. он разлагается на более простые исходы 
.
Пространство элементарных исходов данного случайного опыта 
состоит из шести элементов.
Классическое определение вероятности события. Свойства вероятности события. Примеры.
Вероятностью события называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равновозможных исходов опыта, в котором может появиться это событие. Вероятность события А обозначают через Р (А). В соответствии с определением P(A)=m/n , где m - число элементарных исходов, благоприятствующих событию А; n - число всех равновозможных элементарных исходов опыта, образующих полную группу событий. Это определение вероятности называют классическим.
Основные свойства вероятности. Пусть задано пространство элементарных событий Е , а вероятности Р определены на событиях из Е . Тогда:
Пример 1.
В урне 10 одинаковых по размерам и весу шаров, из которых 4 красных и 6 голубых. из урны извлекается один шар. Какова вероятность того, что извлеченный шар окажется голубым?
Решение. Событие "извлеченный шар оказался голубым" обозначим буквой А. Данное испытание имеет 10 равновозможных элементарных исходов, из которых 6 благоприятствуют событию А. В соответствии с формулой P(A)=m/n , получаем P(A)=6/10=0,6