Эффективные методы решения определенных и несобственных интегралов

Данный раздел содержит дополнительные материалы по методам решения определенных и несобственных интегралов. Предполагается, что читатель владеет средними или высокими навыками интегрирования. Если это не так, пожалуйста, начните с азов: Неопределенный интеграл, примеры решений.

Где неопределенный интеграл – там неподалёку и Определенный интеграл, с формулой Ньютона-Лейбница вы тоже должны быть знакомы не понаслышке. Кроме того, уметь решать простейшие задачи на вычисление площади плоской фигуры (см. 7.2.3.) и на вычисление объёма тела вращения (см. 7.2.4.).

Урок предназначен для тех, кто хочет научиться быстрее и эффективнее решать определенные и несобственные интегралы. Сначала рассмотрим особенности интегрирования четной и нечетной функции по симметричному относительно нуля интервалу. Затем мы разберем задачу о нахождении площади круга с помощью определенного интеграла. Эта задача важна еще и тем, что знакомит вас с распространенным приемом интегрирования определенного интеграла – тригонометрической подстановкой. Она еще нигде не рассматривалась – новый материал!

Аналогично, рассмотрим несобственные интегралы от четных и нечетных функций по симметричному интервалу. В том числе, более редкие типы несобственных интегралов, которые не вошли в основной материал предыдущих разделов: когда нижний предел стремится к «минус бесконечности», когда оба предела стремятся к бесконечности, когда в обоих концах отрезка интегрирования функция терпит бесконечный разрыв (это уже интеграл второго рода). И совсем редкий несобственный интеграл – с точкой разрыва на отрезке интегрирования.

Метод решения определенного интеграла от четной функции по симметричному относительно нуля отрезку

Рассмотрим определенный интеграл вида

.

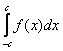Легко заметить, что отрезок интегрирования [-c; c] симметричен относительно нуля.

Если подынтегральная функция f(x) является чётной, то интеграл

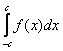
можно вычислить по половине отрезка, а результат – удвоить:

.

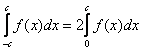Многие догадались, почему это так, но рассмотрим конкретный пример с чертежом:

Пример 1

Вычислить определенный интеграл

.

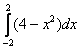О чётности функции много говорилось в методическом материале Графики и свойства элементарных функций. Повторим ещё раз: функция является чётной, если для неё выполняется равенство f(-x) = f(x).

Как проверить функцию на чётность? Нужно вместоx подставить -x.

В данном случае: 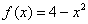и .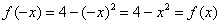

Значит, данная функция является чётной.

Согласно правилу, на симметричном относительно нуля отрезке [-2; 2] наш интеграл от чётной функции можно вычислить следующим образом:

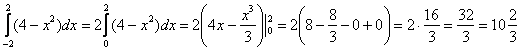
А сейчас геометрическая интерпретация. Да, продолжаем мучить несчастную параболу….

Любая чётная функция, в частности 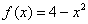, симметрична относительно оси OY:

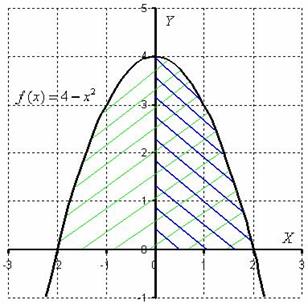
Определенный интеграл

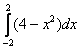
численно равен площади плоской фигуры, которая заштрихована зеленым цветом. Но, в силу чётности подынтегральной функции, а, значит, и симметричности её графика относительно оси OY, достаточно вычислить площадь фигуры, заштрихованной синим цветом, а результат – удвоить. Одинаковые половинки есть геометрическое выражение свойства четности. Именно поэтому справедливо действие

.

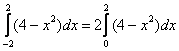Аналогичная история происходит с любой чётной функцией f(x) по симметричному относительно нуля отрезку:

.

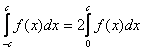Некоторые скажут: «Да зачем это всё нужно, можно ведь и так вычислить определенный интеграл». Можно. Давайте вычислим:

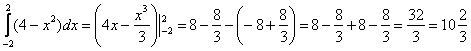
Но удобно ли было подставлять отрицательный нижний предел? Не очень-то. Кстати, ненулевой процент студентов допустит ошибку в знаках. Гораздо проще и приятнее подставить ноль. Заметим, что это еще был простой демонстрационный пример, на практике всё бывает хуже.

Кроме того, рассматриваемый прием часто применяется при вычислении двойных интегралов, тройных интегралов, где вычислений и так хватает.

Короткий пример для самостоятельного решения:

Пример 2

Вычислить определенный интеграл

.

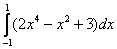Полное решение и ответ в конце урока.

Обратите внимание, что когда вам предложено просто вычислить определенный интеграл, то чертеж выполнять не нужно! Рисунок к Примеру 1 дан только для того, чтобы было понятно правило. Как раз данному моменту посвящена следующая простая задачка:

Пример 3

3.1. Вычислить определенный интеграл

.

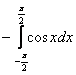3.2. Вычислить площадь плоской фигуры, ограниченной линиями

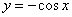, и осью OX на интервале .

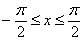Это две разные задачи!Сначала разберемся с первым пунктом:

1) Подынтегральная функция является чётной, отрезок интегрирования симметричен относительно нуля, поэтому:

.

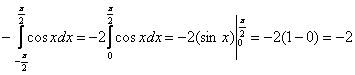Определенный интеграл получился отрицательным и так бывает!

Теперь найдем площадь плоской фигуры. Вот здесь без чертежа обойтись трудно:

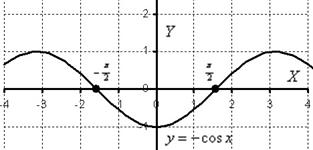
На отрезке 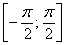график функции расположен ниже оси OX, поэтому:

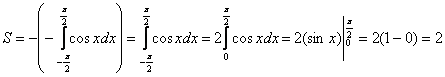
Площадь не может быть отрицательной, именно поэтому в формуле вычисления площади добавляют минус (см. также Пример 3 из раздела 7.2.3.).

Заметьте, что чётность косинуса никто не отменял, поэтому мы опять разделили отрезок и удвоили интеграл.